
Difference: IntegerProgramming (1 vs. 23)
Revision 232018-11-23 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 53 to 53 | ||||||||
| -- TWikiAdminGroup - 20 Feb 2008 | ||||||||
| Deleted: | ||||||||
| < < |
| |||||||
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 222009-10-09 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 14 to 14 | ||||||||
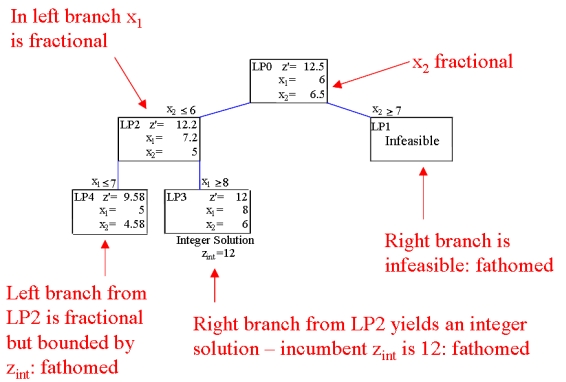
| This branching process results in the formation of a branch-and-bound tree (we will discuss the bounding next). Each node in this tree represents a linear programme consisting of the original linear programme and the extra branches added. Eventually all the leaf nodes in the tree will contain solutions where all the integer variables have integer values (an integer solution) and no further branching is needed. All these values can be compared and the best one is the solution to the original integer programme. | ||||||||
| Changed: | ||||||||
| < < | Note For mixed integer programmes of any reasonable size this tree could be huge, in fact it grows exponentially as the number of integer variables increases. | |||||||
| > > | Note For mixed integer programmes of any reasonable size this tree could be huge; in fact it grows exponentially as the number of integer variables increases. | |||||||
| The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimisation principle: Adding constraints to a mathematical programme will result in a deterioration of the optimal objective value. | ||||||||
Revision 212008-05-07 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 36 to 36 | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | ||||||||
Integer Programming with OR Software | ||||||||
Revision 202008-05-07 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 36 to 36 | ||||||||
| Added: | ||||||||
| > > | ||||||||
Integer Programming with OR Software | ||||||||
Revision 192008-04-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 38 to 38 | ||||||||
Integer Programming with OR Software | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | ||||||||
| ||||||||
Revision 182008-04-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 33 to 33 | ||||||||
Integer Programming Topics | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | ||||||||
Integer Programming with OR Software | ||||||||
Revision 172008-04-22 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> | ||||||||
| Line: 35 to 35 | ||||||||
Integer Programming Topics
| ||||||||
| Added: | ||||||||
| > > | ||||||||
Integer Programming with OR Software
| ||||||||
Revision 162008-03-20 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review - done - Lauren--> Integer Programming | ||||||||
| Changed: | ||||||||
| < < | Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and currently a lot of research is focussing on finding "good"... - Lauren there is a lot of current research finding "good" ways to solve integer programmes. | |||||||
| > > | Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and currently a lot of research is focussing on finding "good" ways to solve integer programmes. | |||||||
Integer programming, the process of solving a (mixed) integer programme, was originally done using the branch-and-bound process. The branch part of the process eliminated non-integer values for integer variables in the following way:
| ||||||||
| Line: 23 to 23 | ||||||||
The current best integer solution is called the incumbent. After solving a linear programme at a leaf node of the branch-and-bound tree one of the following conditions holds:
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
| ||||||||
| Deleted: | ||||||||
| < < |
| |||||||
| Only the last condition requires more branching, all the other conditions result in the node becoming fathomed and no more branching is required from that node. | ||||||||
| Line: 34 to 33 | ||||||||

Integer Programming Topics | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
Integer Programming with OR Software | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
Revision 152008-03-09 - LaurenJackson
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Changed: | ||||||||
| < < | <-- Ready to Review --> | |||||||
| > > | <-- Ready to Review - done - Lauren--> | |||||||
Integer Programming | ||||||||
Revision 142008-03-09 - LaurenJackson
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 16 to 16 | ||||||||
| Note For mixed integer programmes of any reasonable size this tree could be huge, in fact it grows exponentially as the number of integer variables increases. | ||||||||
| Changed: | ||||||||
| < < | The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimization principle: Adding constraints to a mathematical programming will result in a deterioration of the optimal objective value. | |||||||
| > > | The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimisation principle: Adding constraints to a mathematical programme will result in a deterioration of the optimal objective value. | |||||||
| This means that adding the branching constraints to the linear programmes at the branch-and-bound tree nodes will mean the resulting nodes will have an optimal objective function value that is equal to or worse than the optimal objective function value of the original linear programme. Thus the objective function values get worse the deeper into the tree you look. Since we are finding the integer solution in the branch-and-bound tree with the best objective value, we can use any integer solutions to bound the tree. | ||||||||
| Line: 34 to 34 | ||||||||

Integer Programming Topics | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > |
| |||||||
Integer Programming with OR Software | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > |
| |||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
Revision 132008-03-09 - LaurenJackson
Revision 122008-02-29 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 43 to 43 | ||||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
| Changed: | ||||||||
| < < | Results from OpsRes web retrieved at 16:47 (GMT)<--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> Number of topics: 10 <--/patternSearchResultCount--> | |||||||
| > > | Results from OpsRes web retrieved at 16:47 (GMT)<--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> \usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return... <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> Number of topics: 10 <--/patternSearchResultCount--> | |||||||
-- TWikiAdminGroup - 20 Feb 2008
| ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
| |||||||
Revision 112008-02-25 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 25 to 25 | ||||||||
| ||||||||
| Added: | ||||||||
| > > |
| |||||||
| Only the last condition requires more branching, all the other conditions result in the node becoming fathomed and no more branching is required from that node. | ||||||||
Revision 102008-02-24 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Deleted: | ||||||||
| < < | <-- Under Construction --> | |||||||
Integer ProgrammingInteger programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding "good" ways to solve integer programmes. | ||||||||
Revision 92008-02-24 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 38 to 38 | ||||||||
Integer Programming with OR Software | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | ||||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
Revision 82008-02-24 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 37 to 37 | ||||||||
| Changed: | ||||||||
| < < | Integer Programming with OR Software ??? Note to Mike -> parent these from the guides to the OR Software ??? | |||||||
| > > | Integer Programming with OR Software | |||||||
Revision 72008-02-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Added: | ||||||||
| > > |
<-- Under Construction --> | |||||||
Integer ProgrammingInteger programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding "good" ways to solve integer programmes. | ||||||||
Revision 62008-02-21 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Added: | ||||||||
| > > | <-- Ready to Review --> | |||||||
Integer ProgrammingInteger programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding "good" ways to solve integer programmes. | ||||||||
Revision 52008-02-20 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming | ||||||||
| Line: 30 to 30 | ||||||||
 | ||||||||
| Changed: | ||||||||
| < < | Advanced Integer Programming Topics | |||||||
| > > | Integer Programming Topics | |||||||
Revision 42008-02-20 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming | ||||||||
| Line: 34 to 34 | ||||||||
| Changed: | ||||||||
| < < | Integer Programming with OR Software | |||||||
| > > | Integer Programming with OR Software ??? Note to Mike -> parent these from the guides to the OR Software ??? | |||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
Revision 32008-02-20 - TWikiAdminUser
| Line: 1 to 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Integer Programming | |||||||||
| Changed: | |||||||||
| < < | Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes may need to have only integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables and integer variables they are often known as mixed integer programmes. While the change from linear programming is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding “good” ways to solve integer programmes. | ||||||||
| > > | Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding "good" ways to solve integer programmes.
Integer programming, the process of solving a (mixed) integer programme, was originally done using the branch-and-bound process. The branch part of the process eliminated non-integer values for integer variables in the following way:
| ||||||||
| Deleted: | |||||||||
| < < | Integer programming (the process of solving a (mixed) integer programme) was originally done using the branch-and-bound process. The branch part of the process eliminated non-integer values for integer variables in the following way:
*Note* For MIPs of any reasonable size this tree could be huge, in fact it grows exponentially as the number of integer variables increases. The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimization principle: Adding constraints to a mathematical programming will result in a deterioration of the optimal objective value. | ||||||||
| This means that adding the branching constraints to the linear programmes at the branch-and-bound tree nodes will mean the resulting nodes will have an optimal objective function value that is equal to or worse than the optimal objective function value of the original linear programme. Thus the objective function values get worse the deeper into the tree you look. Since we are finding the integer solution in the branch-and-bound tree with the best objective value, we can use any integer solutions to bound the tree. | |||||||||
| Changed: | |||||||||
| < < | The current best integer solution is called the incumbent. After solving a linear programme at a leaf node of the branch-and-bound tree one of the following conditions holds:
| ||||||||
| > > | The current best integer solution is called the incumbent. After solving a linear programme at a leaf node of the branch-and-bound tree one of the following conditions holds:
| ||||||||
| Changed: | |||||||||
| < < | Only the last condition requires more branching, all the other conditions result in the node becoming fathomed and no more branching is required from that node. | ||||||||
| > > | Example of a branch-and-bound tree | ||||||||
| Changed: | |||||||||
| < < | Example
| ||||||||
| > > | 
Advanced Integer Programming TopicsInteger Programming with OR SoftwareTo see integer programming in action, check out some of the integer programming case studies: | ||||||||
Results from OpsRes web retrieved at 16:47 (GMT)<--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> Number of topics: 10 <--/patternSearchResultCount-->-- TWikiAdminGroup - 20 Feb 2008 | |||||||||
| Added: | |||||||||
| > > |
| ||||||||
Revision 22008-02-20 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Added: | ||||||||
| > > | Integer ProgrammingInteger programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes may need to have only integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables and integer variables they are often known as mixed integer programmes. While the change from linear programming is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and there is a lot of current research finding “good” ways to solve integer programmes. Integer programming (the process of solving a (mixed) integer programme) was originally done using the branch-and-bound process. The branch part of the process eliminated non-integer values for integer variables in the following way:
*Note* For MIPs of any reasonable size this tree could be huge, in fact it grows exponentially as the number of integer variables increases. The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimization principle: Adding constraints to a mathematical programming will result in a deterioration of the optimal objective value. This means that adding the branching constraints to the linear programmes at the branch-and-bound tree nodes will mean the resulting nodes will have an optimal objective function value that is equal to or worse than the optimal objective function value of the original linear programme. Thus the objective function values get worse the deeper into the tree you look. Since we are finding the integer solution in the branch-and-bound tree with the best objective value, we can use any integer solutions to bound the tree. The current best integer solution is called the incumbent. After solving a linear programme at a leaf node of the branch-and-bound tree one of the following conditions holds:
Example
Results from OpsRes web retrieved at 16:47 (GMT)<--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> <--/twikiTopRow--> <--/twikiSummary--> <--/twikiBottomRow--> <--/patternSearchResult--> Number of topics: 10 <--/patternSearchResultCount--> | |||||||
| -- TWikiAdminGroup - 20 Feb 2008 \ No newline at end of file | ||||||||
Revision 12008-02-20 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Added: | ||||||||
| > > |
| |||||||
View topic | History: r23 < r22 < r21 < r20 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback
