| |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | | |*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
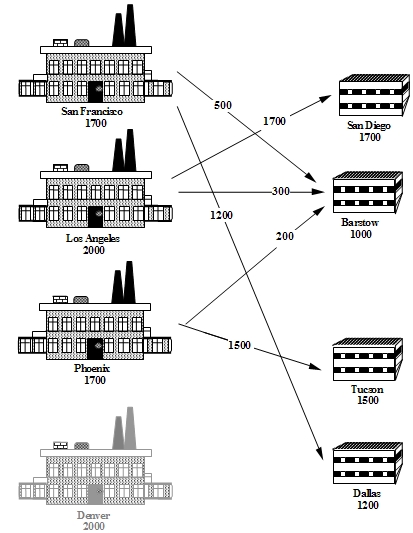
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][Figure 1] gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][Figure 1] gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
| | |
<
< | |*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can further constraint branchs to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.| | >
> | |*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can further constraint branchs to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| |
|*FORM FIELD StudentTasks*|StudentTasks|
- Solve the Cosmic Computers Problem. Write a management summary of your solution.
What to hand in Your management summary.
- Experts Only Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.
| | | |
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1208929978" name="cosmic_badbranch.jpg" path="cosmic_badbranch.jpg" size="127425" stream="cosmic_badbranch.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1208929242" name="cosmic_display.jpg" path="cosmic_display.jpg" size="94525" stream="cosmic_display.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | | |*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][Figure 1] gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][Figure 1] gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
| | |
<
< | |*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 | | | >
> | |*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can further constraint branchs to continue searching from this node:
 | | | | | |*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.|
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1208929978" name="cosmic_badbranch.jpg" path="cosmic_badbranch.jpg" size="127425" stream="cosmic_badbranch.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | | | |
<
< |
- cosmic_graphical.jpg:

| | |
| META FORM |
name="OpsRes.CaseStudyForm" |
| FORM FIELD Title |
Title |
The Cosmic Computers Problem |
| FORM FIELD DateSubmitted |
DateSubmitted |
16 Feb 2008 |
| | | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 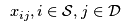 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 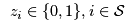 that are 1 if  exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 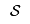 , 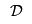 ,  , etc except that the fixed costs  also needs to be specified.
|
|*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers Problem:

The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][ LP relaxation] using option relax_integrality 1.

Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide .

This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens ( Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):

The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:

Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):

Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| | |
<
< | |*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][*Figure 1*] gives a graphical solution to the Cosmic Computers Problem.
|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 | | | >
> | |*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][Figure 1] gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of
|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 | | | | | |*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.|
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1208929978" name="cosmic_badbranch.jpg" path="cosmic_badbranch.jpg" size="127425" stream="cosmic_badbranch.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1208929242" name="cosmic_display.jpg" path="cosmic_display.jpg" size="94525" stream="cosmic_display.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="h" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="h" comment="" date="1208931763" name="cosmic_down.jpg" path="cosmic_down.jpg" size="81517" stream="cosmic_down.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="h" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="h" comment="" date="1208929727" name="cosmic_nocuts.jpg" path="cosmic_nocuts.jpg" size="113819" stream="cosmic_nocuts.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="h" comment="" date="1208929580" name="cosmic_noheur.jpg" path="cosmic_noheur.jpg" size="95913" stream="cosmic_noheur.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="h" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="h" comment="" date="1208931727" name="cosmic_relax_build.jpg" path="cosmic_relax_build.jpg" size="48242" stream="cosmic_relax_build.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1208928168" name="cosmic_relaxation.jpg" path="cosmic_relaxation.jpg" size="71697" stream="cosmic_relaxation.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1208927871" name="cosmic_solution.jpg" path="cosmic_solution.jpg" size="88332" stream="cosmic_solution.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1208931743" name="cosmic_up.jpg" path="cosmic_up.jpg" size="82630" stream="cosmic_up.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="latex69f3b8e9febc7d2c4bbed71def826eba.png" attr="h" comment="" date="1208861162" name="latex69f3b8e9febc7d2c4bbed71def826eba.png" stream="GLOB(0x9aa5acc)" tmpFilename="latex69f3b8e9febc7d2c4bbed71def826eba.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexcd65b9eb27a57506af2eb9c0571ea274.png" attr="h" comment="" date="1208861162" name="latexcd65b9eb27a57506af2eb9c0571ea274.png" stream="GLOB(0x99db86c)" tmpFilename="latexcd65b9eb27a57506af2eb9c0571ea274.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex123a88c971d702f169bd9e1085d356d7.png" attr="h" comment="" date="1208861162" name="latex123a88c971d702f169bd9e1085d356d7.png" stream="GLOB(0x9aa5c10)" tmpFilename="latex123a88c971d702f169bd9e1085d356d7.png" user="BaseUserMapping_333" version="1" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | | | |
>
> |
- cosmic_graphical.jpg:

| | |
| META FORM |
name="OpsRes.CaseStudyForm" |
| FORM FIELD Title |
Title |
The Cosmic Computers Problem |
| FORM FIELD DateSubmitted |
DateSubmitted |
16 Feb 2008 |
| | |
|*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
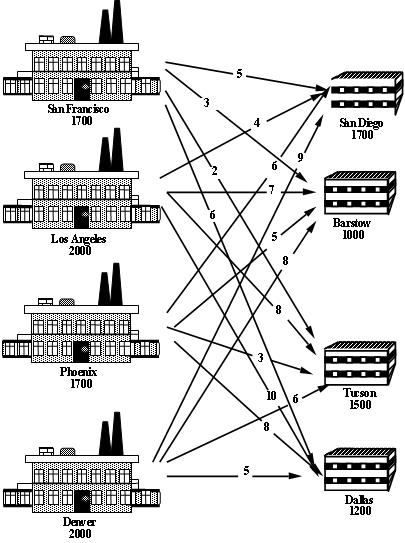 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 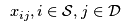 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 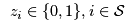 that are 1 if 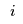 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 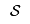 , 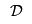 ,  , etc except that the fixed costs  also needs to be specified.
| | |
<
< | |*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).| | >
> | |*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][*Figure 1*] gives a graphical solution to the Cosmic Computers Problem.
|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. [[#fig1][*Figure 1*] gives a graphical solution to the Cosmic Computers Problem.
| | | | |*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.|
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1208929978" name="cosmic_badbranch.jpg" path="cosmic_badbranch.jpg" size="127425" stream="cosmic_badbranch.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic.mod" attr="" comment="" date="1208927396" name="cosmic.mod" path="cosmic.mod" size="1506" stream="cosmic.mod" tmpFilename="" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="cosmic.dat" attr="" comment="" date="1208927408" name="cosmic.dat" path="cosmic.dat" size="818" stream="cosmic.dat" tmpFilename="" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="cosmic.run" attr="" comment="" date="1208927465" name="cosmic.run" path="cosmic.run" size="586" stream="cosmic.run" tmpFilename="" user="MichaelOSullivan" version="1" |
| |
>
> |
| META FILEATTACHMENT |
attachment="cosmic_graphical.jpg" attr="h" comment="" date="1208931299" name="cosmic_graphical.jpg" path="cosmic_graphical.jpg" size="80208" stream="cosmic_graphical.jpg" tmpFilename="" user="MichaelOSullivan" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | | |*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 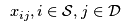 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 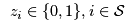 that are 1 if 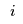 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 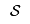 , 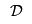 ,  , etc except that the fixed costs  also needs to be specified.
|
|*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| | |
<
< | |*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][_LP relaxation_] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][_LP relaxation_] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.| | >
> | |*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 226400) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the Extra for Experts we will see another technique called constraint branching.|
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the Extra for Experts we will see another technique called constraint branching.| | | | |*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.| | |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1203156443" name="cosmic_badbranch.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" size="64506" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1208929978" name="cosmic_badbranch.jpg" path="cosmic_badbranch.jpg" size="127425" stream="cosmic_badbranch.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1208929242" name="cosmic_display.jpg" path="cosmic_display.jpg" size="94525" stream="cosmic_display.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="h" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="h" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="h" comment="" date="1203156703" name="cosmic_nocuts.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" size="59172" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="h" comment="" date="1203156742" name="cosmic_noheur.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" size="50886" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="h" comment="" date="1208929727" name="cosmic_nocuts.jpg" path="cosmic_nocuts.jpg" size="113819" stream="cosmic_nocuts.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="h" comment="" date="1208929580" name="cosmic_noheur.jpg" path="cosmic_noheur.jpg" size="95913" stream="cosmic_noheur.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="h" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1208928168" name="cosmic_relaxation.jpg" path="cosmic_relaxation.jpg" size="71697" stream="cosmic_relaxation.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1208927871" name="cosmic_solution.jpg" path="cosmic_solution.jpg" size="88332" stream="cosmic_solution.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
|*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
| | |
<
< | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 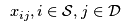 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 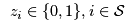 that are 1 if 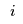 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 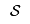 ,  ,  , etc except that the fixed costs  also needs to be specified.
|
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file ( cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;

The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.

Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide .

This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens ( Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):

The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:

Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):

The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.| | >
> | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 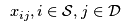 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 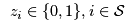 that are 1 if 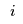 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 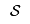 , 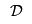 ,  , etc except that the fixed costs  also needs to be specified.
|
|*FORM FIELD ComputationalModel*|ComputationalModel|Since a transportation problem is embedded within the Cosmic Computers problem, we will start with the AMPl model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i] * Build[i];
Finally, we change the MeetDemand constraints:
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] >= Demand[j];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
|
|*FORM FIELD Results*|Results|Using cosmic.run we can solve the Cosmic Computers problem:

The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][_LP relaxation_] using option relax_integrality 1.

Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide .

This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens ( Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):

The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:

Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):

The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.| | | | |*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.|
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1203156443" name="cosmic_badbranch.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" size="64506" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1203156579" name="cosmic_display.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" size="55270" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1208929242" name="cosmic_display.jpg" path="cosmic_display.jpg" size="94525" stream="cosmic_display.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="h" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="h" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="h" comment="" date="1203156703" name="cosmic_nocuts.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" size="59172" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="h" comment="" date="1203156742" name="cosmic_noheur.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" size="50886" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="h" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1208928168" name="cosmic_relaxation.jpg" path="cosmic_relaxation.jpg" size="71697" stream="cosmic_relaxation.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1208927871" name="cosmic_solution.jpg" path="cosmic_solution.jpg" size="88332" stream="cosmic_solution.jpg" tmpFilename="" user="MichaelOSullivan" version="2" |
| | |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex69f3b8e9febc7d2c4bbed71def826eba.png" attr="h" comment="" date="1208861162" name="latex69f3b8e9febc7d2c4bbed71def826eba.png" stream="GLOB(0x9aa5acc)" tmpFilename="latex69f3b8e9febc7d2c4bbed71def826eba.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexcd65b9eb27a57506af2eb9c0571ea274.png" attr="h" comment="" date="1208861162" name="latexcd65b9eb27a57506af2eb9c0571ea274.png" stream="GLOB(0x99db86c)" tmpFilename="latexcd65b9eb27a57506af2eb9c0571ea274.png" user="BaseUserMapping_333" version="1" |
| | |
| META FILEATTACHMENT |
attachment="latexcd2cee3fedd0238e50b11d84c331e985.png" attr="h" comment="" date="1208861453" name="latexcd2cee3fedd0238e50b11d84c331e985.png" stream="GLOB(0xa4b4a50)" tmpFilename="latexcd2cee3fedd0238e50b11d84c331e985.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex5ec19384f577119fa936dcc6fb49d9e3.png" attr="h" comment="" date="1208861453" name="latex5ec19384f577119fa936dcc6fb49d9e3.png" stream="GLOB(0xa4b49fc)" tmpFilename="latex5ec19384f577119fa936dcc6fb49d9e3.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex4e85da8e3e178be2bf661a6ca694df55.png" attr="h" comment="" date="1208919192" name="latex4e85da8e3e178be2bf661a6ca694df55.png" stream="GLOB(0x8f6dd88)" tmpFilename="latex4e85da8e3e178be2bf661a6ca694df55.png" user="MichaelOSullivan" version="1" |
| |
>
> |
| META FILEATTACHMENT |
attachment="latexe1bee7b21d544faefa6098fc522d595e.png" attr="h" comment="" date="1208927379" name="latexe1bee7b21d544faefa6098fc522d595e.png" stream="GLOB(0xa9028d4)" tmpFilename="latexe1bee7b21d544faefa6098fc522d595e.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="cosmic.mod" attr="" comment="" date="1208927396" name="cosmic.mod" path="cosmic.mod" size="1506" stream="cosmic.mod" tmpFilename="" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="cosmic.dat" attr="" comment="" date="1208927408" name="cosmic.dat" path="cosmic.dat" size="818" stream="cosmic.dat" tmpFilename="" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="cosmic.run" attr="" comment="" date="1208927465" name="cosmic.run" path="cosmic.run" size="586" stream="cosmic.run" tmpFilename="" user="MichaelOSullivan" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
| META FILEATTACHMENT |
attachment="latexb4af6a1247e105b14d11b8236fec3bb3.png" attr="h" comment="" date="1208861452" name="latexb4af6a1247e105b14d11b8236fec3bb3.png" stream="GLOB(0xa4b4b1c)" tmpFilename="latexb4af6a1247e105b14d11b8236fec3bb3.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexcd2cee3fedd0238e50b11d84c331e985.png" attr="h" comment="" date="1208861453" name="latexcd2cee3fedd0238e50b11d84c331e985.png" stream="GLOB(0xa4b4a50)" tmpFilename="latexcd2cee3fedd0238e50b11d84c331e985.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex5ec19384f577119fa936dcc6fb49d9e3.png" attr="h" comment="" date="1208861453" name="latex5ec19384f577119fa936dcc6fb49d9e3.png" stream="GLOB(0xa4b49fc)" tmpFilename="latex5ec19384f577119fa936dcc6fb49d9e3.png" user="BaseUserMapping_333" version="1" |
| |
>
> |
| META FILEATTACHMENT |
attachment="latex4e85da8e3e178be2bf661a6ca694df55.png" attr="h" comment="" date="1208919192" name="latex4e85da8e3e178be2bf661a6ca694df55.png" stream="GLOB(0x8f6dd88)" tmpFilename="latex4e85da8e3e178be2bf661a6ca694df55.png" user="MichaelOSullivan" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
|*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
| | |
<
< | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 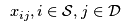 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 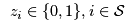 that are 1 if 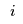 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
\[ \min \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} + \sum_{i \in {\cal S}} C_i z_i \]
3. Formulate the Constraints
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. Identify the data
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
| | >
> | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 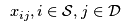 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 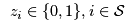 that are 1 if 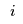 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
% \[ \sum_{j \in {\cal D}} x_{ij} = s_i z_i, i \in {\cal S} \]%
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 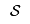 , 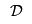 ,  , etc except that the fixed costs  also needs to be specified.
| | | |
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file (cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).| | | |
| META FILEATTACHMENT |
attachment="latex123a88c971d702f169bd9e1085d356d7.png" attr="h" comment="" date="1208861162" name="latex123a88c971d702f169bd9e1085d356d7.png" stream="GLOB(0x9aa5c10)" tmpFilename="latex123a88c971d702f169bd9e1085d356d7.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexca50954408b19cb112dbda0d63cf4b6f.png" attr="h" comment="" date="1208861163" name="latexca50954408b19cb112dbda0d63cf4b6f.png" stream="GLOB(0x9aa01b4)" tmpFilename="latexca50954408b19cb112dbda0d63cf4b6f.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex0ac921cfeb8cc8edc4830a6460a447d4.png" attr="h" comment="" date="1208861163" name="latex0ac921cfeb8cc8edc4830a6460a447d4.png" stream="GLOB(0x99db398)" tmpFilename="latex0ac921cfeb8cc8edc4830a6460a447d4.png" user="BaseUserMapping_333" version="1" |
| |
>
> |
| META FILEATTACHMENT |
attachment="latexbf08ef72db56e75f9d190a1caddac925.png" attr="h" comment="" date="1208861389" name="latexbf08ef72db56e75f9d190a1caddac925.png" stream="GLOB(0xa3781e8)" tmpFilename="latexbf08ef72db56e75f9d190a1caddac925.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexb4af6a1247e105b14d11b8236fec3bb3.png" attr="h" comment="" date="1208861452" name="latexb4af6a1247e105b14d11b8236fec3bb3.png" stream="GLOB(0xa4b4b1c)" tmpFilename="latexb4af6a1247e105b14d11b8236fec3bb3.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexcd2cee3fedd0238e50b11d84c331e985.png" attr="h" comment="" date="1208861453" name="latexcd2cee3fedd0238e50b11d84c331e985.png" stream="GLOB(0xa4b4a50)" tmpFilename="latexcd2cee3fedd0238e50b11d84c331e985.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex5ec19384f577119fa936dcc6fb49d9e3.png" attr="h" comment="" date="1208861453" name="latex5ec19384f577119fa936dcc6fb49d9e3.png" stream="GLOB(0xa4b49fc)" tmpFilename="latex5ec19384f577119fa936dcc6fb49d9e3.png" user="BaseUserMapping_333" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
|*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
| | |
<
< | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
s have supply nodes Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK??? transportation.mod model file and see what changes we need to make.
1. IDENTIFY THE DECISION VARIABLES
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
This is specified by Flow in transportation.mod.
We need to add ???LINK??? binary variables to transportation.mod (rename it cosmic.mod) for determining if a plant is built or not:
# Do we build a SUPPLY_NODE or not?
var Build {SUPPLY_NODES} binary default 1;
2. FORMULATE THE OBJECTIVE FUNCTION
We have already incorporated the transportation cost in transportation.mod, now we have to add the fixed (construction + maintenance) cost:
# The cost of building a SUPPLY_NODE
param BuildCost {SUPPLY_NODES};
# The objective is to minimise the total cost (transportation + build)
minimize TotalCost:
sum {s in SUPPLY_NODES, t in DEMAND_NODES}
Cost[s, t] * Flow[s, t] +
sum {s in SUPPLY_NODES} BuildCost[s] * Build[s];
3. FORMULATE THE CONSTRAINTS
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. IDENTIFY THE DATA
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
|
Latex rendering error!! dvi file was not created.
| >
> | |*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 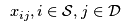 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 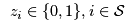 that are 1 if 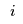 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
\[ \min \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} + \sum_{i \in {\cal S}} C_i z_i \]
3. Formulate the Constraints
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. Identify the data
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
| | | |
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file (cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).| | | |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
<
< |
| META FILEATTACHMENT |
attachment="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" attr="h" comment="" date="1208860589" name="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" stream="GLOB(0xa5c9728)" tmpFilename="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" user="BaseUserMapping_333" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="latex69f3b8e9febc7d2c4bbed71def826eba.png" attr="h" comment="" date="1208861162" name="latex69f3b8e9febc7d2c4bbed71def826eba.png" stream="GLOB(0x9aa5acc)" tmpFilename="latex69f3b8e9febc7d2c4bbed71def826eba.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexcd65b9eb27a57506af2eb9c0571ea274.png" attr="h" comment="" date="1208861162" name="latexcd65b9eb27a57506af2eb9c0571ea274.png" stream="GLOB(0x99db86c)" tmpFilename="latexcd65b9eb27a57506af2eb9c0571ea274.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex123a88c971d702f169bd9e1085d356d7.png" attr="h" comment="" date="1208861162" name="latex123a88c971d702f169bd9e1085d356d7.png" stream="GLOB(0x9aa5c10)" tmpFilename="latex123a88c971d702f169bd9e1085d356d7.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latexca50954408b19cb112dbda0d63cf4b6f.png" attr="h" comment="" date="1208861163" name="latexca50954408b19cb112dbda0d63cf4b6f.png" stream="GLOB(0x9aa01b4)" tmpFilename="latexca50954408b19cb112dbda0d63cf4b6f.png" user="BaseUserMapping_333" version="1" |
| META FILEATTACHMENT |
attachment="latex0ac921cfeb8cc8edc4830a6460a447d4.png" attr="h" comment="" date="1208861163" name="latex0ac921cfeb8cc8edc4830a6460a447d4.png" stream="GLOB(0x99db398)" tmpFilename="latex0ac921cfeb8cc8edc4830a6460a447d4.png" user="BaseUserMapping_333" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
| |
<
< | |*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company who wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|*FORMULATION*
This problem is essentially a ???LINK??? transportation problem, but with ???LINK??? master-slave constraints at the supply nodes. Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK???
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|*FORMULATION*
This problem is essentially a ???LINK??? transportation problem, but with ???LINK??? master-slave constraints at the supply nodes. Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK??? transportation.mod model file and see what changes we need to make.
1. IDENTIFY THE DECISION VARIABLES
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
This is specified by Flow in transportation.mod.
We need to add ???LINK??? binary variables to transportation.mod (rename it cosmic.mod) for determining if a plant is built or not:
# Do we build a SUPPLY_NODE or not?
var Build {SUPPLY_NODES} binary default 1;
2. FORMULATE THE OBJECTIVE FUNCTION
We have already incorporated the transportation cost in transportation.mod, now we have to add the fixed (construction + maintenance) cost:
# The cost of building a SUPPLY_NODE
param BuildCost {SUPPLY_NODES};
# The objective is to minimise the total cost (transportation + build)
minimize TotalCost:
sum {s in SUPPLY_NODES, t in DEMAND_NODES}
Cost[s, t] * Flow[s, t] +
sum {s in SUPPLY_NODES} BuildCost[s] * Build[s];
3. FORMULATE THE CONSTRAINTS
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. IDENTIFY THE DATA
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
| | >
> | |*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
s have supply nodes Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK???
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
s have supply nodes Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK??? transportation.mod model file and see what changes we need to make.
1. IDENTIFY THE DECISION VARIABLES
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
This is specified by Flow in transportation.mod.
We need to add ???LINK??? binary variables to transportation.mod (rename it cosmic.mod) for determining if a plant is built or not:
# Do we build a SUPPLY_NODE or not?
var Build {SUPPLY_NODES} binary default 1;
2. FORMULATE THE OBJECTIVE FUNCTION
We have already incorporated the transportation cost in transportation.mod, now we have to add the fixed (construction + maintenance) cost:
# The cost of building a SUPPLY_NODE
param BuildCost {SUPPLY_NODES};
# The objective is to minimise the total cost (transportation + build)
minimize TotalCost:
sum {s in SUPPLY_NODES, t in DEMAND_NODES}
Cost[s, t] * Flow[s, t] +
sum {s in SUPPLY_NODES} BuildCost[s] * Build[s];
3. FORMULATE THE CONSTRAINTS
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. IDENTIFY THE DATA
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
|
Latex rendering error!! dvi file was not created.
| | |
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file (cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).| | | |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
>
> |
| META FILEATTACHMENT |
attachment="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" attr="h" comment="" date="1208860589" name="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" stream="GLOB(0xa5c9728)" tmpFilename="latex38b6586d69f948fea8e1cc9e6cb1dc4a.png" user="BaseUserMapping_333" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
| |
<
< |
| >
> |
| | |
| |
<
< | |*FORM FIELD ProblemDescription*|ProblemDescription|*THE COMPUTER PLANT PROBLEM*
Consider the Cosmic Computer company who wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?| | >
> | |*FORM FIELD ProblemDescription*|ProblemDescription|The Cosmic Computer company who wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?| | | | |*FORM FIELD ProblemFormulation*|ProblemFormulation|*FORMULATION*
This problem is essentially a ???LINK??? transportation problem, but with ???LINK??? master-slave constraints at the supply nodes. Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK??? transportation.mod model file and see what changes we need to make.
1. IDENTIFY THE DECISION VARIABLES
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
This is specified by Flow in transportation.mod.
We need to add ???LINK??? binary variables to transportation.mod (rename it cosmic.mod) for determining if a plant is built or not:
# Do we build a SUPPLY_NODE or not?
var Build {SUPPLY_NODES} binary default 1;
2. FORMULATE THE OBJECTIVE FUNCTION
We have already incorporated the transportation cost in transportation.mod, now we have to add the fixed (construction + maintenance) cost:
# The cost of building a SUPPLY_NODE
param BuildCost {SUPPLY_NODES};
# The objective is to minimise the total cost (transportation + build)
minimize TotalCost:
sum {s in SUPPLY_NODES, t in DEMAND_NODES}
Cost[s, t] * Flow[s, t] +
sum {s in SUPPLY_NODES} BuildCost[s] * Build[s];
3. FORMULATE THE CONSTRAINTS
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. IDENTIFY THE DATA
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
|
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file (cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):
 The first integer solution (with
The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the
The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.| | |
<
< |
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="" comment="" date="1203156443" name="cosmic_badbranch.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" size="64506" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="" comment="" date="1203156579" name="cosmic_display.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" size="55270" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="" comment="" date="1203156703" name="cosmic_nocuts.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" size="59172" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="" comment="" date="1203156742" name="cosmic_noheur.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" size="50886" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| >
> |
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="h" comment="" date="1203156443" name="cosmic_badbranch.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" size="64506" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="h" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="h" comment="" date="1203156579" name="cosmic_display.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" size="55270" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="h" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="h" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="h" comment="" date="1203156703" name="cosmic_nocuts.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" size="59172" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="h" comment="" date="1203156742" name="cosmic_noheur.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" size="50886" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="h" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="h" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="h" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="h" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| | |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
Return to top | |
<
< | Computational Model | >
> | Computational Model | | |
Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| | |
Return to top | |
<
< | Results | >
> | Results | | |
Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then an integer solution is found quickly with 6 cuts. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic;
- A repair heuristic that tries to from integer solutions from fractional ones;
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 Now the LP relaxation
Now the LP relaxation Node 0 is solved, but then cuts are generated (indicated by Node 0+) and after 2 cuts are added an integer solution is found, shown by *. After 9 cuts are generated another integer solution is found (hence another *) and this is the optimal solution. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching. | | |
Return to top | |
<
< | Conclusions | >
> | Conclusions | | |
As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
| META FORM |
name="OpsRes.CaseStudyForm" |
| |
<
< |
| >
> |
| FORM FIELD Title |
Title |
The Cosmic Computers Problem |
| | |
| | |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| |
>
> |
| META TOPICMOVED |
by="MichaelOSullivan" date="1204454668" from="OpsRes.AFacilityLocationProblem" to="OpsRes.CosmicComputersProblem" |
|
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
Application Areas: Industrial Planning
Contents | |
<
< | | >
> | | | | Problem Description
The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
Where should the company set up their plants to minimise their total costs (fixed plus transportation)? | | | Return to top
Problem Formulation | |
<
< | This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 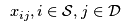 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 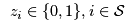 that are 1 if 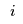 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 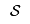 , 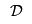 ,  , etc except that the fixed costs  also needs to be specified.
| >
> |
This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 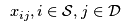 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 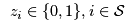 that are 1 if 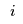 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 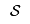 , 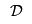 ,  , etc except that the fixed costs  also needs to be specified.
| | |
Return to top
Computational Model | |
<
< | Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| >
> |
Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| | |
Return to top
Results | |
<
< | Using cosmic.run we can solve the Cosmic Computers Problem:
<img src= | >
> |
Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then an integer solution is found quickly with 6 cuts. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic;
- A repair heuristic that tries to from integer solutions from fractional ones;
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 Now the LP relaxation
Now the LP relaxation Node 0 is solved, but then cuts are generated (indicated by Node 0+) and after 2 cuts are added an integer solution is found, shown by *. After 9 cuts are generated another integer solution is found (hence another *) and this is the optimal solution. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching. | | |
Return to top
Conclusions | |
<
< | As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
<a name= | >
> |
As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem

| | |
Return to top
| |
<
< | | >
> | <--
Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either 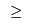 3 or 3 or 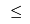 2. First, let's branch up: 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can add further constraint branches to continue searching from this node:
 -->
--> | | |
| |
<
< | | >
> | <--
- Solve the Cosmic Computers Problem. Write a management summary of your solution.
What to hand in Your management summary.
- Experts Only Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.
--> | | | |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
Application Areas: Industrial Planning
Contents | |
<
< | | >
> | | | | Problem Description
The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
Return to top
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
Return to top | |
<
< | Problem Formulation | >
> | Problem Formulation | | | | |
<
< | This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 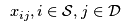 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 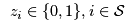 that are 1 if 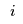 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 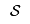 , 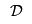 ,  , etc except that the fixed costs  also needs to be specified.
| >
> | This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 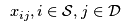 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 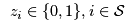 that are 1 if 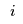 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 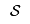 , 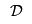 ,  , etc except that the fixed costs  also needs to be specified.
| | | | |
<
< | Return to top
Computational Model | >
> | Return to top | | | | |
<
< | Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| >
> | Computational Model | | | | |
<
< | Return to top
Results | >
> | Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
| | | | |
<
< | Using cosmic.run we can solve the Cosmic Computers Problem:
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using option relax_integrality 1.
 Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide . .
 This shows that
This shows that Node 0 (the LP relaxation) is solved, then an integer solution is found quickly with 6 cuts. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic;
- A repair heuristic that tries to from integer solutions from fractional ones;
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens (Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):
 Now the LP relaxation
Now the LP relaxation Node 0 is solved, but then cuts are generated (indicated by Node 0+) and after 2 cuts are added an integer solution is found, shown by *. After 9 cuts are generated another integer solution is found (hence another *) and this is the optimal solution. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:
 Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):
 Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching. | >
> | Return to top | | | | |
<
< | Return to top
Conclusions | >
> | Results | | | | |
<
< | As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 | >
> | Using cosmic.run we can solve the Cosmic Computers Problem:
<img src= | | | | |
<
< | Return to top | >
> | Return to top
Conclusions
As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
<a name=
Return to top | | | | |
<
< | Extra for Experts | >
> | | | | | |
<
< | Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:
 The sum of the three non-zero
The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either 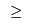 3 or 3 or 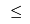 2. First, let's branch up: 2. First, let's branch up:
 Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional Build variables. We can add further constraint branches to continue searching from this node:
 | >
> | | | | | |
<
< | Return to top | >
> | | | | | |
<
< | Student Tasks | >
> | | | | | |
<
< |
- Solve the Cosmic Computers Problem. Write a management summary of your solution.
What to hand in Your management summary.
- Experts Only Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.
| >
> | | | | | |
<
< | Return to top | >
> | | | |
| |
>
> |
| | |
|*FORM FIELD ProblemDescription*|ProblemDescription|*THE COMPUTER PLANT PROBLEM*
Consider the Cosmic Computer company who wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?| |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
| |
>
> | <-- Under Construction --> | | |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
|
>
> |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<--
This template controls both the look and functionality of case study topics.
You should not need to alter the layout, only edit the data using the form above.
Set the view and edit templates:
Comment out the next line to use the TWiki default view
Comment out the next line to use the TWiki default edit
-->
<--
This topic can only be changed by:
-->
Case Study: The Cosmic Computers Problem
Submitted: 16 Feb 2008
Application Areas: Industrial Planning
Contents
Problem Description
The Cosmic Computer company wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:
 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
Return to top
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
Return to top
Problem Formulation
This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Let's go through the mathematical programming formulation steps and consider what changes we might have to make.
1. Identify the Decision Variables
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
The flow variables 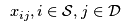 determine where to ship the computers, so we need to add binary variables that govern which of the supply nodes exist, i.e., 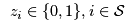 that are 1 if 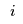 exists and 0 otherwise.
2. Formulate the Objective Function
The cost of transporting good through the network is already incorporated into the transportation problem objective, now we have to add the fixed (construction + maintenance) cost  :
3. Formulate the Constraints
The constraints are the same as the transportation problem formulation, except that the supply is determined by the construction (or not) of a plant:
and we need to (at least) meet demand, but the formulation no longer needs to be balanced (otherwise we would always build all our construction plants):
4. Identify the data
The data in this problem is the same as that required for a transportation problem, i.e., 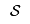 , 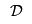 ,  , etc except that the fixed costs  also needs to be specified.
Computational Model
Since a transportation problem is embedded within the Cosmic Computers Problem, we will start with the AMPL model file transportation.mod (see The Transportation Problem in AMPL for details):
set SUPPLY_NODES;
set DEMAND_NODES;
param Supply {SUPPLY_NODES} >= 0, integer;
param Demand {DEMAND_NODES} >= 0, integer;
param Cost {SUPPLY_NODES, DEMAND_NODES} default 0;
param Lower {SUPPLY_NODES, DEMAND_NODES}
integer default 0;
param Upper {SUPPLY_NODES, DEMAND_NODES}
integer default Infinity;
var Flow {i in SUPPLY_NODES, j in DEMAND_NODES}
>= Lower[i, j], <= Upper[i, j], integer;
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] = Supply[i];
subject to MeetDemand {j in DEMAND_NODES}:
sum {i in SUPPLY_NODES} Flow[i, j] = Demand[j];
We add new decision variables that decide if we build the production plants or not:
var Build {SUPPLY_NODES} binary;
We define a new parameter for the fixed cost (of construction + maintenance):
param FixedCost {SUPPLY_NODES};
We incorporate the fixed cost into the objective function and the Build variables into the supply constraints and change the supply constraints since the problem may not be balanced:
minimize TotalCost:
sum {i in SUPPLY_NODES, j in DEMAND_NODES}
Cost[i, j] * Flow[i, j] +
sum {i in SUPPLY_NODES} FixedCost[i] * Build[i];
subject to UseSupply {i in SUPPLY_NODES}:
sum {j in DEMAND_NODES} Flow[i, j] <= Supply[i] * Build[i];
The final model file is given in cosmic.mod.
The data file cosmic.dat is straight forward.
We can also adapt transportation.run by removing all the balancing AMPL commands, e.g., param difference;. We add a different check to cosmic.run that ensures there is enough supply to satisfy the demand (otherwise the problem is infeasible):
check : sum {s in SUPPLY_NODES} Supply[s] >= sum {d in DEMAND_NODES} Demand[d];
Return to top
Results
Using cosmic.run we can solve the Cosmic Computers Problem:

The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using option relax_integrality 1.

Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on setting CPLEX options in AMPL see ILOG's AMPL CPLEX User Guide .

This shows that Node 0 (the LP relaxation) is solved, then an integer solution is found quickly with 6 cuts. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic;
- A repair heuristic that tries to from integer solutions from fractional ones;
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX options rinsheur -1 and repairtries -1) and see what happens ( Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of your changes will not be obvious):

Now the LP relaxation Node 0 is solved, but then cuts are generated (indicated by Node 0+) and after 2 cuts are added an integer solution is found, shown by *. After 9 cuts are generated another integer solution is found (hence another *) and this is the optimal solution. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (try "integer programming cut" on Google), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:

Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):

Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.
Return to top
Conclusions
As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 Return to top
Return to top
Extra for Experts
Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:

The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. We can remove the fractional part by forcing this sum to be either 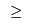 3 or 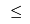 2. First, let's branch up:

Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:

This solution still has fractional Build variables. We can add further constraint branches to continue searching from this node:
 Return to top
Return to top
Student Tasks
- Solve the Cosmic Computers Problem. Write a management summary of your solution.
What to hand in Your management summary.
- Experts Only Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.
Return to top
|*FORM FIELD ProblemDescription*|ProblemDescription|*THE COMPUTER PLANT PROBLEM*
Consider the Cosmic Computer company who wish to set up production in America. They are contemplating building production plants in up to 4 locations. Each location has planning restrictions that effectively determine the monthly production possible in each location. The monthly fixed costs of the different locations have been calculated by the accounting department, and are listed below:
These plants will supply stores at 4 locations. Predicted demand and per-unit transport costs for supplying the 4 production plants to the 4 stores are shown below, along with the quantity each factory can supply:

Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
There is a recycling tax being proposed by the San Francisco mayor that would place a tax rate of 15% to 20% of the transportation cost of any computers leaving San Francisco. Cosmic Computers have agreed that the recycling tax is a valid proposition, but are lobbying the mayor to keep it low. If the tax rate is too high they will not build a production plant (and create jobs) in San Francisco. What is the highest tax rate that will result in Cosmic Computers building a production plant in San Francisco?
The Denver mayor is very keen for Cosmic Computers to build a production plant in Denver. He has offered property tax rebates for Cosmic Computers if they build in Denver. What is maximum fixed cost for a production plant in Denver that will result in the construction of the plant?|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|*FORMULATION*
This problem is essentially a ???LINK??? transportation problem, but with ???LINK??? master-slave constraints at the supply nodes. Since we don't want to use all our supply (as we might not build all our plants), let's start with the unbalanced ???LINK??? transportation.mod model file and see what changes we need to make.
1. IDENTIFY THE DECISION VARIABLES
The decisions are two-fold:
- Where to build the plants?
- Where to ship the computers?
This is specified by Flow in transportation.mod.
We need to add ???LINK??? binary variables to transportation.mod (rename it cosmic.mod) for determining if a plant is built or not:
# Do we build a SUPPLY_NODE or not?
var Build {SUPPLY_NODES} binary default 1;
2. FORMULATE THE OBJECTIVE FUNCTION
We have already incorporated the transportation cost in transportation.mod, now we have to add the fixed (construction + maintenance) cost:
# The cost of building a SUPPLY_NODE
param BuildCost {SUPPLY_NODES};
# The objective is to minimise the total cost (transportation + build)
minimize TotalCost:
sum {s in SUPPLY_NODES, t in DEMAND_NODES}
Cost[s, t] * Flow[s, t] +
sum {s in SUPPLY_NODES} BuildCost[s] * Build[s];
3. FORMULATE THE CONSTRAINTS
The constraints are the same as in transportatioon.mod, except that the supply is determined by the construction (or not) of a plant:
# Flow must not exceed supply
subject to EnoughSupply {s in SUPPLY_NODES}:
sum {t in DEMAND_NODES} Flow[s, t] <= Supply[s] * Build[s];
4. IDENTIFY THE DATA
The data file cosmic.dat for this problem is the same as the data for a transportation problem (e.g., brewery.dat), except that the fixed cost also needs to be specified:
param BuildCost :=
'San Francisco' 70000
'Los Angeles' 70000
Phoenix 65000
Denver 70000
;
* POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).|
|*FORM FIELD Results*|Results|Once we have finished composing cosmic.mod and cosmic.dat we can solve using a typical script file ( cosmic.run):
reset;
model cosmic.mod;
data cosmic.dat;
option solver cplex;
solve;
display Build;
display Flow;

The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the ???LINK??? LP relaxation using option relax_integrality 1.

Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process: mipdisplay 2 gives a moderate amount of information about the process and mipinterval 1 displays this information for every node. For detailed information on CPLEX setting in AMPL see ???LINK??? ILOG's AMPL CPLEX User Guide .

This shows that Node 0 (the LP relaxation) is solved, then Node 0+ gives two integer solutions (indicated by *), the final one of which is optimal. There are many methods at work here, including:
- A relaxation induced neighbourhood search (RINS) heuristic (indicated by the
+);
- A repair heuristic (also indicated by a
+ and a comment on repair);
- Application of cuts to the LP relaxation;
- Careful selection of variables to branch on.
The RINS heuristic looks for a feasible integer solution starting from the LP relaxation solution and the repair heuristic looks for a feasible integer solution from the initial values (here all zero). Let's turn the heuristics off (CPLEX option rinsheur -1 and repairtries -1) and see what happens ( Note To see the true effect of these changes you will have to make changes to your script file, restart AMPL and run your script again. Otherwise, AMPL will use your old solution and the effect of you changes will not be obvious):

The first integer solution (with TotalCost = 230282) is no longer found (as it was the result of the RINS heuristic), but applying cuts still gives an integer solution without any branch-and-bound nodes. Cuts are linear constraints that are added to the LP relaxation to remove fractional solutions. There is a vast amount of literature on cuts for integer programming (google "integer programming cut"), but we will not delve into it here. Let's turn off all the cuts (CPLEX option mipcuts -1) and see what happens:

Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching varaible. Here, it branches on Build['Denver'] even though this variable is integer in the LP relaxation. Instead of using the default CPLEX selection rules for the branching variable, let's branch on the fractional variable that is closest to integer (CPLEX option varselect -1):

The Computer Plant Problem has demonstrated many of the "behind the scenes" work that CPLEX does for you. For another example of integer programming in AMPL, see ???LINK??? the Ice Sculptures example . In the ???LINK??? Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|*POST-OPTIMAL ANALYSIS*
Validation
To ensure our solution is valid we simply need to check that the Build variables take integer values (either 0 or 1) and that the shipments from the plants to the stores are within the bounds specified by the construction decisions.
The optimal solution shows that Cosmic Computers will build production plants in San Francisco, but not Denver. We can consider the effect of the tax on transportation by using parametric analysis:
param SFCost {DEMAND_NODES};
let {d in DEMAND_NODES} SFCost[d] := Cost['San Francisco', d];
option omit_zero_rows 1;
option omit_zero_cols 1;
for {t in 0.15..0.20 by 0.005} {
let {d in DEMAND_NODES} Cost['San Francisco', d] := (1 + t) * SFCost[d];
solve;
printf "Tax rate = %g\%\n", t * 100;
display Build, Flow;
}
Note We will have to refine our search range further, e.g., t in 0.17..0.18 by 0.001, to make an accurate estimate of the maximum tax rate.
We can perform a similar parametric analysis on BuildCost['Denver'] to find the maximum price that will result in construction in Denver (and hence how much of a tax rebate the Denver mayor would have to offer).
PRESENTATION OF SOLUTION AND ANALYSIS
Your management summary should contain:
- A brief summary of the problem description;
- A construction plan for the plants;
- A transportation plan that describes the shipments from plants to stores;
- A description of your post-optimal analysis:
- A brief description of the analysis undertaken (and why);
- A summary of the results of your analysis;
IMPLEMENTATION AND ONGOING MONITORING
Before implementation, sensitivity analysis of both the fixed and transportation costs could identify any data that needs to be confirmed before proceeding. This could also identify any problems should construction costs run over budget.
Ongoing monitoring of the transportation costs, production levels (supply) and demands will produce optimal shiiping plans. If the fixed cost at any plant rises significantly, relocation may be considered (this can also take the form of a facility location problem).|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in The Computer Plant Problem the sum of any subset of Build variables should be integer. Consider the LP relaxation solution:

The sum of the three non-zero Build variables is 2.82 (2 dp), but it should be integer. Remove the fractional part by forcing this to be either $\geq$ 3 or $\leq$ 2. First, let's branch up:

Our solution is integer so we can fathom this node. Now let's ???LINK??? drop the Up constraint and branch down:

This solution still has fractional Build variables. We can use another constraint branch to continue searching from this node:
 |
|*FORM FIELD StudentTasks*|StudentTasks| 1 Solve The Computer Plant Problem. Write a management summary of your solution. Be sure to answer all the questions in the problem description.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- Complete the branch-and-bound process using constraint branches on fractional sums of the
Build variables. Draw your branch-and-bound tree as shown above (in the Extra for Experts section). Be sure to indicate what branches you used. Briefly (1 paragraph) compare your experience with constraint branching to the variable branching used in CPLEX.
What to hand in Hand in your drawing of your branch-and-bound tree along with your conclusions about the effectiveness of constraint branching compared with variable branching.|
| META FILEATTACHMENT |
attachment="cosmic_badbranch.jpg" attr="" comment="" date="1203156443" name="cosmic_badbranch.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" size="64506" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_badbranch.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_bbtree.jpg" attr="" comment="" date="1203156533" name="cosmic_bbtree.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" size="31801" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_bbtree.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_display.jpg" attr="" comment="" date="1203156579" name="cosmic_display.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" size="55270" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_display.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_down.jpg" attr="" comment="" date="1203156611" name="cosmic_down.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" size="44148" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_down.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_network.jpg" attr="" comment="" date="1203156662" name="cosmic_network.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" size="52416" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_network.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_nocuts.jpg" attr="" comment="" date="1203156703" name="cosmic_nocuts.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" size="59172" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_nocuts.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_noheur.jpg" attr="" comment="" date="1203156742" name="cosmic_noheur.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" size="50886" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_noheur.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relax_build.jpg" attr="" comment="" date="1203156776" name="cosmic_relax_build.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" size="36711" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relax_build.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_relaxation.jpg" attr="" comment="" date="1203156839" name="cosmic_relaxation.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" size="41815" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_relaxation.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_solution.jpg" attr="" comment="" date="1203156870" name="cosmic_solution.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" size="45055" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_solution.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="cosmic_up.jpg" attr="" comment="" date="1203156902" name="cosmic_up.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" size="40589" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\AFacilityLocProb\cosmic_up.jpg" tmpFilename="" user="LaurenJackson" version="1" |
|
  Copyright © 2008-2026 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding TWiki? Send feedback |
|
|
|

 Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
![\[ \begin{array}{r@{\,}r@{\,}l} \min & \displaystyle \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \displaystyle \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ & \displaystyle \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latexfb2a6bb240be8ce70a8e2d96e8ceb894.png)
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
| The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional  |
| The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional  |
| Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
![\[ \begin{array}{r@{\,}r@{\,}l} \min & \displaystyle \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \displaystyle \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ & \displaystyle \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latexfb2a6bb240be8ce70a8e2d96e8ceb894.png)
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
|*FORM FIELD Conclusions*|Conclusions|As with the Brewery Problem, the solution to the Cosmic Computers Problem can be presented in many ways. Figure 1 gives a graphical solution to the Cosmic Computers Problem.
Figure 1 Solution to the Cosmic Computers Problem
 |
| The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK???  This solution still has fractional
This solution still has fractional  |
| The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
Our solution is integer so we can fathom this node. Now let's drop the Up constraint and branch down:
 This solution still has fractional
This solution still has fractional  |
|![\[ \begin{array}{r@{\,}r@{\,}l} \min & \displaystyle \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \displaystyle \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ & \displaystyle \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latexfb2a6bb240be8ce70a8e2d96e8ceb894.png)
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| |
| |
| The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK???  This solution still has fractional
This solution still has fractional  |
|*FORM FIELD StudentTasks*|StudentTasks|
|
|*FORM FIELD StudentTasks*|StudentTasks| Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
![\[ \begin{array}{r@{\,}r@{\,}l} \min & \displaystyle \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \displaystyle \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ & \displaystyle \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latexfb2a6bb240be8ce70a8e2d96e8ceb894.png)
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| |
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of
|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of  The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK???  This solution still has fractional
This solution still has fractional  |
|*FORM FIELD StudentTasks*|StudentTasks|
|
|*FORM FIELD StudentTasks*|StudentTasks| Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
Where should the company set up their plants to minimise their total costs (fixed plus transportation)?
|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|This problem is a facility location problem where the master-slave constraints control the existence of supply nodes for a transportation problem.
Traditional transportation problem formulations are as follows:
![\[ \begin{array}{r@{\,}r@{\,}l} \min & \displaystyle \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \displaystyle \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ & \displaystyle \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latexfb2a6bb240be8ce70a8e2d96e8ceb894.png)
 The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the [[LPRelaxation][LP relaxation] using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  The first integer solution (with
The first integer solution (with  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using
The output shows that CPLEX has not required any branch-and-bound nodes again. Is this problem also naturally integer? We can check by solving the LP relaxation using  Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:
Unfortunately, our problem is not naturally integer. CPLEX performs a lot of "clever tricks" to solve mixed-integer programmes quickly. Let's look at the effect of some of these techniques.
First, we can see what is happening in the branch-and-bound tree by setting the CPLEX options for displaying the branch-and-bound process:  This shows that
This shows that  Now the LP relaxation
Now the LP relaxation  Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on
Here the optimal integer solution is found at the second node and then the rest of the tree (6 branch-and-bound nodes in all) is used to ensure this is the optimum. CPLEX is very careful with its selection of a branching variable. Here, it branches on  Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.|
Notice that the branch-and-bound tree is larger (8 nodes as opposed to 6), so this selection strategy did not work as well as the CPLEX default.
While solving the Cosmic Computers Problem we have explored many of the "behind the scenes" work that CPLEX does for you. See Integer Programming with AMPL for more examples. In the Extra for Experts we will see another technique called constraint branching.| |
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of
|
|*FORM FIELD ExtraForExperts*|ExtraForExperts|Another form of branch and bound implements branches on constraints that should take integer values. For example, in the Cosmic Computers Problem the sum of any subset of  The sum of the three non-zero
The sum of the three non-zero  Our solution is integer so we can fathom this node. Now let's ???LINK???
Our solution is integer so we can fathom this node. Now let's ???LINK???  This solution still has fractional
This solution still has fractional  |
|*FORM FIELD StudentTasks*|StudentTasks|
|
|*FORM FIELD StudentTasks*|StudentTasks|![\[ \begin{array}{r@{\,}r@{\,}l} \min & \sum_{i \in {\cal S}} \sum_{j \in {\cal D}} c_{ij} & x_{ij} \\ \text{subject to} & \sum_{j \in {\cal D}} & x_{ij} = s_i, i \in {\cal S} \\ \sum_{i \in {\cal S}} & x_{ij} = d_j, j \in {\cal D} \end{array} \]](/pub/OpsRes/CosmicComputersProblem/latex82544f4458fed84231b56c8eaa5aa942.png)