Facility Location Problems

Facility location problems are a classical example of the use of master-slave constraints.

The following definition of the general facility location problem is from J. E. Beasley's OR-Notes.

The general facility location problem is: given a set of facility locations and a set of customers who are served from the facilities then:

• which facilities should be used;
• which customers should be served from which facilities so as to minimise the total cost of serving all the customers.

Given the set of facilities and the set of customers , we can define binary (0-1) variables:

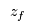1. = 1 if facility 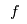is used, 0 otherwise;
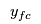2. = 1 if facility 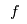serves customer 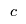, 0 otherwise.

Now the following master-slave constraint ensures that facility only serves customers if it is used:

(1)

The decision variables, objective function and constraints vary depending on the problem, but similar master-slave constraints are always present in facility location problems.

We will not delve into it here, but a "tighter" formulation would use the following constraints instead of (1):

Facility Location Case Studies

Results from OpsRes web retrieved at 06:58 (GMT)

-- TWikiAdminGroup - 22 Apr 2008