
Difference: WhiskasCatFoodProblem (55 vs. 56)
Revision 562019-07-20 - TWikiAdminUser
| Line: 1 to 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> <-- This template controls both the look and functionality of case study topics. You should not need to alter the layout, only edit the data using the form above. Set the view and edit templates: Comment out the next line to use the TWiki default view
<-- This topic can only be changed by:
Case Study: The Whiskas Cat Food ProblemSubmitted: 31 Jan 2008Operations Research Topics: LinearProgramming, BlendingModelsApplication Areas: Pet Food ManufacturingContentsProblem DescriptionFigure 1 Whiskas cat food label Whiskas cat food (shown in Figure 1) is manufactured by Uncle Ben's. Uncle Ben's want to produce their cat food products as cheaply as possible while ensuring they meet the stated nutritional analysis requirements shown on the cans (see Figure 2). Thus they want to vary the quantities of each ingredient used (the main ingredients being chicken, beef, mutton, rice, wheat and gel) while still meeting their nutritional standards (see Figure 3).
Figure 2 Ingredients and nutritional requirements
Whiskas cat food (shown in Figure 1) is manufactured by Uncle Ben's. Uncle Ben's want to produce their cat food products as cheaply as possible while ensuring they meet the stated nutritional analysis requirements shown on the cans (see Figure 2). Thus they want to vary the quantities of each ingredient used (the main ingredients being chicken, beef, mutton, rice, wheat and gel) while still meeting their nutritional standards (see Figure 3).
Figure 2 Ingredients and nutritional requirements
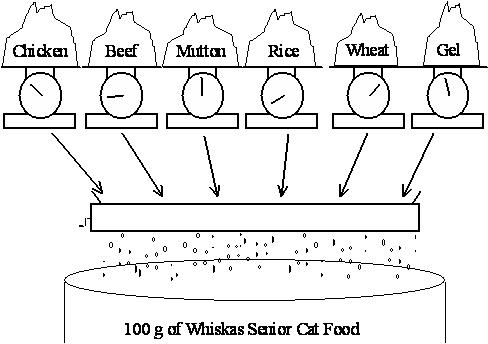 The costs of the chicken, beef, and mutton are $0.013, $0.008 and $0.010 respectively, while the costs of the rice, wheat and gel are $0.002, $0.005 and $0.001 respectively. (All costs are per gram.) In this case study, we will ignore the vitamin and mineral ingredients. (Any costs for these are likely to be very small anyway.)
Each ingredient contributes to the total weight of protein, fat, fibre and salt in the final product. The contributions (in grams) per gram of ingredient are given in Table 1.
Table 1 Contributions of ingredients
The costs of the chicken, beef, and mutton are $0.013, $0.008 and $0.010 respectively, while the costs of the rice, wheat and gel are $0.002, $0.005 and $0.001 respectively. (All costs are per gram.) In this case study, we will ignore the vitamin and mineral ingredients. (Any costs for these are likely to be very small anyway.)
Each ingredient contributes to the total weight of protein, fat, fibre and salt in the final product. The contributions (in grams) per gram of ingredient are given in Table 1.
Table 1 Contributions of ingredients
Problem FormulationWe will formulate the Whiskas Cat Food Problem as a mathematical programme (using the 4 key steps). 1. Identify the Decision Variables
For the Whiskas Cat Food Problem the decisions are the grams of each of the different ingredients we include in the can.
We must formally define our decision variables, being sure to state the units we are using.
2. Formulate the Objective Function

For the Whiskas Cat Food Problem the objective is to minimise the total cost of ingredients per can of cat food.
We know the cost per g of each ingredient, so we can define our objective: to minimise the total cost of a can
3. Formulate the Constraints
The constraints for the Whiskas Cat Food Problem are that:
4. Identify the data
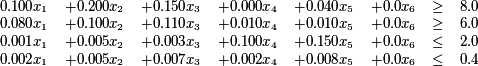
We know the total weight of the can. We also know the cost of the ingredients, the nutritional analysis requirements and the contribution (per gram) of each ingredient in terms of the nutritional analysis. This is enough to formulate the necessary mathematical programme. However, we will reconsider our data after solving the mathematical programme and performing some analysis.
Generalising the FormulationThe previous formulation will solve the Whiskas Cat Food Problem for the given ingredients and requirements, however we would have to reformulate if a new ingredient or requirement was added. We can "abstract" the data to make our formulation more general and thus easier to modify when the data changes. LetComputational ModelUsing our original formulation, the computational model in AMPL would have been time consuming (and repetitive!) to create, e.g.,var x1 >= 0; # Amount (g) of chicken meat used in a can of cat food var x2 >= 0; # Amount (g) of beef used in a can of cat food . . . var x6 >= 0; # Amount (g) of gel used in a can of cat food (= g)Note that the # is used for commenting.
However, we can easily translate our generalised formulation into AMPL. First, we define the sets for the ingredients and requirements
set INGREDIENTS; set REQUIREMENTS;We will see later how to "populate" these sets using an AMPL data file. Using the sets we can define the decision variables
var Amount {INGREDIENTS} >= 0;
parameters for the costs
param Cost {INGREDIENTS};
and the objective function
minimize TotalCost : sum {i in INGREDIENTS} Cost[i] * Amount[i];
Now we have a variable that determines the amount (in g) of each ingredient (whatever they may be) in a can of Whiskas and our objective is to minimize the total unit cost of producing the cans (although we haven't specified the actual costs yet).
Next, we need to define parameters for the contribution each ingredient makes to the requirements and for the bounds on the requirements themselves
param Contributes {REQUIREMENTS, INGREDIENTS};
param Lower {REQUIREMENTS} default -Infinity;
param Upper {r in REQUIREMENTS} >= Lower[r], default Infinity;
Note the use of a bound to ensure that Upper Lower and default values for the requirement bounds.
Finally, we can formulate the constraints in AMPL
subject to MeetRequirements {r in REQUIREMENTS} :
Lower[r] <= sum {i in INGREDIENTS} Contributes[r, i] * Amount[i] <= Upper[r];
Now our AMPL model is complete (see whiskas.mod for a complete AMPL model file).
Once an AMPL model file is complete, we need to create a data file to create an "instance" of this problem. Note that we can use several different data files with the same model file (in practice this means solving the same mathematical programme with different data).
First, create a new data file for AMPL and save it as whiskas.dat.
Next, all our AMPL expressions rely on the sets INGREDIENTS and REQUIREMENTS, so we will define these first. Remember, when AMPL is in data mode (see The AMPL Process), we don't need to enclose set elements with ' and ' (unless there is a whitespace{ and } to signify the start and end of a set.
We can define the sets of ingredients and requirements using the set keyword and the assignment operator :=
set INGREDIENTS := CHICKEN BEEF MUTTON RICE WHEAT GEL ; set REQUIREMENTS := PROTEIN FAT FIBRE SALT ONECAN ;Note Since whitespace signifies the end of a symbol, you need space before the terminating ;.
Now the set of ingredients has been established, we can assign data to parameters that use that set.
First, define the parameter Cost
param Cost := CHICKEN 0.013 BEEF 0.008 ... GEL 0.001 ;Then, use a transposed table to define the nutritional contribution per gram for the ingredients
param Contributes (tr):
PROTEIN FAT FIBRE SALT ONECAN :=
CHICKEN 0.100 0.080 0.001 0.002 1.0
BEEF 0.200 0.100 0.005 0.005 1.0
MUTTON 0.150 0.110 0.003 0.007 1.0
RICE 0.000 0.010 0.100 0.002 1.0
WHEAT 0.040 0.010 0.150 0.008 1.0
GEL 0.0 0.0 0.0 0.0 1.0
;
Finally, we can define both the Lower and Upper parameters
param Lower := PROTEIN 8.0 FAT 6.0 ONECAN 100 ; param Upper := FIBRE 2.0 SALT 0.4 ONECAN 100 ;Now our data file whiskas.dat is complete. Now we can use AMPL to determine how to optimally mix the ingredients in a can of cat food. First, start a command line application and navigate to the directory where you saved whiskas.mod and whiskas.dat. Then start AMPL.
Create the model in AMPL by typing:
model whiskas.mod;Populate the model with data by typing: data whiskas.dat;Choose the CPLEX solver option solver cplex;and solve The Whiskas Cat Food Problem using AMPL: solve;To see the amount (in g) of each ingredient to include in the 100g can: display Amount;When you are developing a model and running it many times (while testing and debugging) you might like to create a script file. For the Whiskas Cat Food Problem your script file whiskas.run will be:
reset; model whiskas.mod; data whiskas.dat; option solver cplex; solve; display Amount;Remember, you can run the script file in AMPL with the command: include whiskas.run;Return to top ResultsRunningwhiskas.run gives the following output:
ampl: include whiskas.run;
CPLEX 10.1.0: optimal solution; objective 0.52
2 dual simplex iterations (0 in phase I)
Amount [*] :=
BEEF 60
CHICKEN 0
GEL 40
MUTTON 0
RICE 0
WHEAT 0
;
This solution indicates that the mix of ingredients for minimising the cost of a can of Whiskas cat food is to use 60g of beef and 40g of gel. The cost of the can will be 52c.
For the Whiskas Cat Food Problem we will not perform any post-optimal analysis. <-- However, this is the example case study for SensitivityAnalysis and ParametricAnalysis. -->Validation To validate our solution for the Whiskas Cat Food Problem, we can do a quick check that our solution makes sense. First, the amounts should add up to the weight of the can (e.g., 60g + 40g = 100g). If not, there is something wrong. Next, we can do a quick check of the constraints to ensure none of them are violated. For large models you won't always be able to check the solution by hand. However, you can use AMPL expressions to quickly calculate quantities needed for validation.
ampl: display {r in REQUIREMENTS} sum {i in INGREDIENTS} Contributes[r, i] * Amo
unt[i];
sum{i in INGREDIENTS} Contributes[r,i]*Amount[i] [*] :=
FAT 6
FIBRE 0.3
ONECAN 100
PROTEIN 12
SALT 0.3
;
ampl: display Lower, Upper;
: Lower Upper :=
FAT 6 Infinity
FIBRE -Infinity 2
ONECAN 100 100
PROTEIN 8 Infinity
SALT -Infinity 0.4
;
The final validation is to write up a management summary for your manager and/or client and see if they think your solution is a valid one. If they identify some (or all) of the solution that is not valid, then you should discuss with them the reasons why it is invalid and start a "feedback" loop in the Operations Research methodology.
Return to top
ConclusionsThe solution for the Whiskas Cat Food Problem is a simple one to summarise. Here is the management summary for the Whiskas Cat Food Problem. Important When presenting your solution you must be careful about the number of decimal places you use. You should not use a greater accuracy than your data allows. Return to top<-- --> <--
 Whiskas cat food (shown in Figure 1) is manufactured by Uncle Ben's. Uncle Ben's want to produce their cat food products as cheaply as possible while ensuring they meet the stated nutritional analysis requirements shown on the cans (see Figure 2). Thus they want to vary the quantities of each ingredient used (the main ingredients being chicken, beef, mutton, rice, wheat and gel) while still meeting their nutritional standards (see Figure 3).
Figure 2 Ingredients and nutritional requirements
Whiskas cat food (shown in Figure 1) is manufactured by Uncle Ben's. Uncle Ben's want to produce their cat food products as cheaply as possible while ensuring they meet the stated nutritional analysis requirements shown on the cans (see Figure 2). Thus they want to vary the quantities of each ingredient used (the main ingredients being chicken, beef, mutton, rice, wheat and gel) while still meeting their nutritional standards (see Figure 3).
Figure 2 Ingredients and nutritional requirements
 The costs of the chicken, beef, and mutton are $0.013, $0.008 and $0.010 respectively, while the costs of the rice, wheat and gel are $0.002, $0.005 and $0.001 respectively. (All costs are per gram.) In this case study, we will ignore the vitamin and mineral ingredients. (Any costs for these are likely to be very small anyway.)
Each ingredient contributes to the total weight of protein, fat, fibre and salt in the final product. The contributions (in grams) per gram of ingredient are given in Table 1.
Table 1 Contributions of ingredients
The costs of the chicken, beef, and mutton are $0.013, $0.008 and $0.010 respectively, while the costs of the rice, wheat and gel are $0.002, $0.005 and $0.001 respectively. (All costs are per gram.) In this case study, we will ignore the vitamin and mineral ingredients. (Any costs for these are likely to be very small anyway.)
Each ingredient contributes to the total weight of protein, fat, fibre and salt in the final product. The contributions (in grams) per gram of ingredient are given in Table 1.
Table 1 Contributions of ingredients
For the Whiskas Cat Food Problem the decisions are the grams of each of the different ingredients we include in the can.
We must formally define our decision variables, being sure to state the units we are using.
2. Formulate the Objective Function

For the Whiskas Cat Food Problem the objective is to minimise the total cost of ingredients per can of cat food.
We know the cost per g of each ingredient, so we can define our objective: to minimise the total cost of a can
3. Formulate the Constraints
The constraints for the Whiskas Cat Food Problem are that:
4. Identify the data
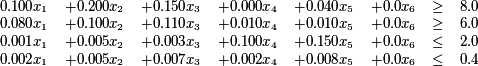
We know the total weight of the can. We also know the cost of the ingredients, the nutritional analysis requirements and the contribution (per gram) of each ingredient in terms of the nutritional analysis. This is enough to formulate the necessary mathematical programme. However, we will reconsider our data after solving the mathematical programme and performing some analysis.
Generalising the FormulationThe previous formulation will solve the Whiskas Cat Food Problem for the given ingredients and requirements, however we would have to reformulate if a new ingredient or requirement was added. We can "abstract" the data to make our formulation more general and thus easier to modify when the data changes. Letvar x1 >= 0; # Amount (g) of chicken meat used in a can of cat food var x2 >= 0; # Amount (g) of beef used in a can of cat food . . . var x6 >= 0; # Amount (g) of gel used in a can of cat food (= g)Note that the # is used for commenting.
However, we can easily translate our generalised formulation into AMPL. First, we define the sets for the ingredients and requirements
set INGREDIENTS; set REQUIREMENTS;We will see later how to "populate" these sets using an AMPL data file. Using the sets we can define the decision variables
var Amount {INGREDIENTS} >= 0;
parameters for the costs
param Cost {INGREDIENTS};
and the objective function
minimize TotalCost : sum {i in INGREDIENTS} Cost[i] * Amount[i];
Now we have a variable that determines the amount (in g) of each ingredient (whatever they may be) in a can of Whiskas and our objective is to minimize the total unit cost of producing the cans (although we haven't specified the actual costs yet).
Next, we need to define parameters for the contribution each ingredient makes to the requirements and for the bounds on the requirements themselves
param Contributes {REQUIREMENTS, INGREDIENTS};
param Lower {REQUIREMENTS} default -Infinity;
param Upper {r in REQUIREMENTS} >= Lower[r], default Infinity;
Note the use of a bound to ensure that Upper Lower and default values for the requirement bounds.
Finally, we can formulate the constraints in AMPL
subject to MeetRequirements {r in REQUIREMENTS} :
Lower[r] <= sum {i in INGREDIENTS} Contributes[r, i] * Amount[i] <= Upper[r];
Now our AMPL model is complete (see whiskas.mod for a complete AMPL model file).
Once an AMPL model file is complete, we need to create a data file to create an "instance" of this problem. Note that we can use several different data files with the same model file (in practice this means solving the same mathematical programme with different data).
First, create a new data file for AMPL and save it as whiskas.dat.
Next, all our AMPL expressions rely on the sets INGREDIENTS and REQUIREMENTS, so we will define these first. Remember, when AMPL is in data mode (see The AMPL Process), we don't need to enclose set elements with ' and ' (unless there is a whitespace{ and } to signify the start and end of a set.
We can define the sets of ingredients and requirements using the set keyword and the assignment operator :=
set INGREDIENTS := CHICKEN BEEF MUTTON RICE WHEAT GEL ; set REQUIREMENTS := PROTEIN FAT FIBRE SALT ONECAN ;Note Since whitespace signifies the end of a symbol, you need space before the terminating ;.
Now the set of ingredients has been established, we can assign data to parameters that use that set.
First, define the parameter Cost
param Cost := CHICKEN 0.013 BEEF 0.008 ... GEL 0.001 ;Then, use a transposed table to define the nutritional contribution per gram for the ingredients
param Contributes (tr):
PROTEIN FAT FIBRE SALT ONECAN :=
CHICKEN 0.100 0.080 0.001 0.002 1.0
BEEF 0.200 0.100 0.005 0.005 1.0
MUTTON 0.150 0.110 0.003 0.007 1.0
RICE 0.000 0.010 0.100 0.002 1.0
WHEAT 0.040 0.010 0.150 0.008 1.0
GEL 0.0 0.0 0.0 0.0 1.0
;
Finally, we can define both the Lower and Upper parameters
param Lower := PROTEIN 8.0 FAT 6.0 ONECAN 100 ; param Upper := FIBRE 2.0 SALT 0.4 ONECAN 100 ;Now our data file whiskas.dat is complete. Now we can use AMPL to determine how to optimally mix the ingredients in a can of cat food. First, start a command line application and navigate to the directory where you saved whiskas.mod and whiskas.dat. Then start AMPL.
Create the model in AMPL by typing:
model whiskas.mod;Populate the model with data by typing: data whiskas.dat;Choose the CPLEX solver option solver cplex;and solve The Whiskas Cat Food Problem using AMPL: solve;To see the amount (in g) of each ingredient to include in the 100g can: display Amount;When you are developing a model and running it many times (while testing and debugging) you might like to create a script file. For the Whiskas Cat Food Problem your script file whiskas.run will be:
reset; model whiskas.mod; data whiskas.dat; option solver cplex; solve; display Amount;Remember, you can run the script file in AMPL with the command: include whiskas.run;| |*FORM FIELD Results*|Results|Running whiskas.run gives the following output:
ampl: include whiskas.run;
CPLEX 10.1.0: optimal solution; objective 0.52
2 dual simplex iterations (0 in phase I)
Amount [*] :=
BEEF 60
CHICKEN 0
GEL 40
MUTTON 0
RICE 0
WHEAT 0
;
This solution indicates that the mix of ingredients for minimising the cost of a can of Whiskas cat food is to use 60g of beef and 40g of gel. The cost of the can will be 52c.
For the Whiskas Cat Food Problem we will not perform any post-optimal analysis. <-- However, this is the example case study for SensitivityAnalysis and ParametricAnalysis. -->Validation To validate our solution for the Whiskas Cat Food Problem, we can do a quick check that our solution makes sense. First, the amounts should add up to the weight of the can (e.g., 60g + 40g = 100g). If not, there is something wrong. Next, we can do a quick check of the constraints to ensure none of them are violated. For large models you won't always be able to check the solution by hand. However, you can use AMPL expressions to quickly calculate quantities needed for validation.
ampl: display {r in REQUIREMENTS} sum {i in INGREDIENTS} Contributes[r, i] * Amo
unt[i];
sum{i in INGREDIENTS} Contributes[r,i]*Amount[i] [*] :=
FAT 6
FIBRE 0.3
ONECAN 100
PROTEIN 12
SALT 0.3
;
ampl: display Lower, Upper;
: Lower Upper :=
FAT 6 Infinity
FIBRE -Infinity 2
ONECAN 100 100
PROTEIN 8 Infinity
SALT -Infinity 0.4
;
The final validation is to write up a management summary for your manager and/or client and see if they think your solution is a valid one. If they identify some (or all) of the solution that is not valid, then you should discuss with them the reasons why it is invalid and start a "feedback" loop in the Operations Research methodology.
|
|*FORM FIELD Conclusions*|Conclusions|The solution for the Whiskas Cat Food Problem is a simple one to summarise.
Here is the management summary for the Whiskas Cat Food Problem.
Important When presenting your solution you must be careful about the number of decimal places you use. You should not use a greater accuracy than your data allows.
|
1. Using
whiskas.mod, whiskas.dat and whiskas.run, solve the Whiskas Cat Food Problem. Write a management summary for your solution.
What to hand in
Your management summary.
2. Find the optimal mix of ingredients if the can weighs 150g and ham is available as an ingredient that costs $0.007 per g and each g of ham contributes 0.180g of protein, 0.110g of fat, 0.002g of fibre and 0.008g of salt. Note The nutritional requirements are expressed as percentages of the can weight so these will change.
Write a management summary for your solution.
What to hand in
Your new data file |
whiskas.dat and your management summary.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Deleted: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| < < |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Added: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| > > |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
View topic | History: r56 < r55 < r54 < r53 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback

