Linear Programming
The simplest type of mathematical programme is a linear programme. For your mathematical programme to be a linear programme you need the following conditions to be true:- The decision variables must be real variables;
- The objective constraint must be a linear expression;
- The constraints must be linear expressions.
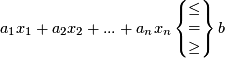
![\[ \begin{array}{rr@{}l} \min & c^\top & x \\ \text{subject to} & A & x \left\{ \begin{matrix} \leq \\ = \\ \geq \end{matrix} \right\} b \end{array} \]](/pub/OpsRes/LinearProgramming/latex1cc802e4d59a591a1d7e77c20f899965.png)
Linear Programming Topics
To see linear programming in action, check out some of the linear programming case studies:Results from OpsRes web retrieved at 10:31 (GMT)
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
Number of topics: 8
-- MichaelOSullivan - 16 Feb 2008 Topic revision: r9 - 2018-11-23 - TWikiAdminUser
Ideas, requests, problems regarding TWiki? Send feedback

