Case Study: The Coke Supply Chain Problem
Submitted: 20 Feb 2008
Application Areas: Logistics, Industrial Planning, Fuel Manufacturing
Contents
Problem Description
THE COKE PRODUCTION PROBLEM
Adapted from a real-world problem
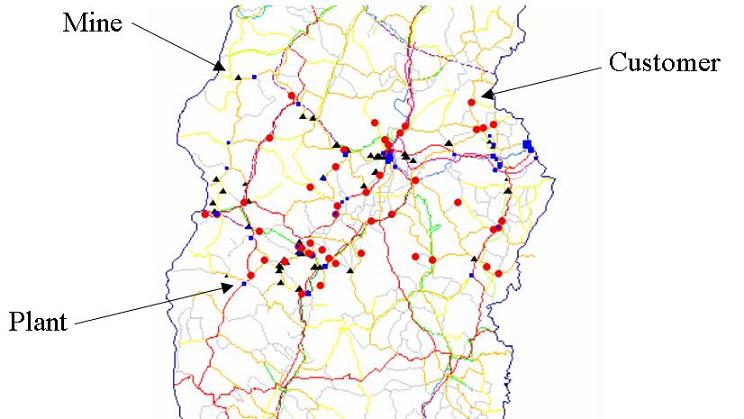
Over 29% of world's coke is made in China. Recently market liberalization has lead to town and village enterprises, with uncertainty in future markets resulting in short-sighted resource use. There are currently many small cokemaking plants with relatively primitive technology. This has resulted in an industry with low transportation costs (as coke is supplied by many small local producers) but high pollution and energy use.
Figure 1 Coke from
en.wikipedia.org/wiki/Image:Koks_Brennstoff.jpg

The government wants to move cokemaking to Shanxi, where they can establish bigger facilities. This plan will be more efficient, with less pollution, but will also result in higher transport costs (calculated from a GIS database). The plants in Shanxi will be built with one or more oven batteries, each making 75,000 tonnes of coke a year. The process these plants will use to convert coal to coke is "thermal decomposition".
This process results in 1 tonne of coke produced for every 1.3 tonnes of coal processed.
The (simplified) problem we will model has the following details:
- There are six coal mines, each able to supply up to a certain amount of coal each year to the plants for processing
- There are six customers, each with a certain demand for coke each year
- There are six possible plant locations, each able to process a certain amount of coke each year
Each plant has 6 possible sizes, with coke processing levels and associated construction costs shown below:
| Size |
Cost |
| (kT/yr) |
(MRMB) |
| 450 |
19.6 |
| 375 |
16.5 |
| 300 |
13.5 |
| 225 |
10.5 |
| 150 |
7.4 |
| 75 |
4.4 |
Each Mine has the following coal supply per year:
| Mine |
1 |
2 |
3 |
4 |
5 |
6 |
| Coal Supply (kT/yr) |
25.8 |
728 |
1456 |
40 |
36.9 |
1100 |
Each Customer has the following coke demand per year:
| Customer |
1 |
2 |
3 |
4 |
5 |
6 |
| Coke Demand (kT/yr) |
83 |
5.5 |
6.975 |
5.5 |
720.75 |
5.5 |
The transportation costs (RMB/kT) between the mines and the
plants are as follows:
| RMB/kT |
Plant 1 |
Plant 2 |
Plant 3 |
Plant 4 |
Plant 5 |
Plant 6 |
| Mine 1 |
231737 |
46813 |
79337 |
195845 |
103445 |
45186 |
| Mine 2 |
179622 |
267996 |
117602 |
200298 |
128184 |
49046 |
| Mine 3 |
45170 |
93159 |
156241 |
218655 |
103802 |
119616 |
| Mine 4 |
149925 |
254305 |
76423 |
123534 |
151784 |
104081 |
| Mine 5 |
152301 |
205126 |
24321 |
66187 |
195559 |
88979 |
| Mine 6 |
223934 |
132391 |
51004 |
122329 |
222927 |
54357 |
The transportation costs (RMB/kT) between the plants and the customers are as follows:
| RMB/kT |
Plant 1 |
Plant 2 |
Plant 3 |
Plant 4 |
Plant 5 |
Plant 6 |
| Customer 1 |
6736 |
42658 |
70414 |
45170 |
184679 |
111569 |
| Customer 2 |
217266 |
227190 |
249640 |
203029 |
153531 |
117487 |
| Customer 3 |
35936 |
28768 |
126316 |
2498 |
130317 |
74034 |
| Customer 4 |
73446 |
52077 |
108368 |
75011 |
49827 |
62850 |
| Customer 5 |
174664 |
177461 |
151589 |
153300 |
59916 |
135162 |
| Customer 6 |
186302 |
189099 |
147026 |
164938 |
149836 |
286307 |
Return to top
Extra for Experts
This problem is similar to
the Cosmic Computers Problem, but the
facility location is a little different. Rather than face a decision about whether to build a plant or not, we need to determine what type of plant to build. This gives rise to the following variable:
While solving the Coke Supply Chain Problem, the expression
will often be fractional. This means that the capacity of the plant
where
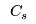
is the capacity of a plant of size
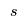
will be between the capacities of two different size plants, e.g., 280 kT/yr is between 225 kT/yr plant and a 300 kT/yr plant. We could use constraints to remove the fractionality, e.g.,
These branches will ensure plants have the right capacities, but will still not resolve fractionalities in the
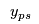
. However, if we want the capacity of plant
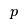
to be
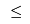
225, then we can remove all the
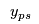
that allow for the capacity to be larger than 225:
Conversely, if we want to branch up, i.e., the capacity is
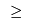
300, then we can remove all the
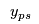
that allow the capacity to be smaller than 300:
Note For these branches to work properly, the possibility of building no plant must be modeled as building a plant with no capacity (i.e.,
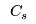
= 0) for no cost.
Return to top
Student Tasks
- Write AMPL model, data and script files (
coke.mod, coke.dat and coke.run respectively) to solve the Coke Production Problem. Write a management summary for your solution.
What to hand in Your 3 AMPL files. Your management summary.
- Experts Only Solve the LP relaxation of the Coke Supply Chain Problem integer programme. Using the branches described in Extra for Experts, use AMPL to perform branching on at least 4 nodes and draw the resulting branch-and-bound tree.
Hint See Extra for Experts in the Cosmic ComputersProblem for an example of constraint branching in AMPL.
What to hand in Your AMPL code for implementing the branches. Your drawing of your branch-and-bound tree.
Return to top
 The government wants to move cokemaking to Shanxi, where they can establish bigger facilities. This plan will be more efficient, with less pollution, but will also result in higher transport costs (calculated from a GIS database). The plants in Shanxi will be built with one or more oven batteries, each making 75,000 tonnes of coke a year. The process these plants will use to convert coal to coke is "thermal decomposition". This process results in 1 tonne of coke produced for every 1.3 tonnes of coal processed.
The (simplified) problem we will model has the following details:
The government wants to move cokemaking to Shanxi, where they can establish bigger facilities. This plan will be more efficient, with less pollution, but will also result in higher transport costs (calculated from a GIS database). The plants in Shanxi will be built with one or more oven batteries, each making 75,000 tonnes of coke a year. The process these plants will use to convert coal to coke is "thermal decomposition". This process results in 1 tonne of coke produced for every 1.3 tonnes of coal processed.
The (simplified) problem we will model has the following details:
 Each plant has 6 possible sizes, with coke processing levels and associated construction costs shown below:
Each plant has 6 possible sizes, with coke processing levels and associated construction costs shown below:
![\[ \begin{array}{r@{\,}l@{\quad\quad}l} \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\leq 225 & \text{(branching down)} \\ \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\geq 300 & \text{(branching up)} \end{array} \]](/pub/OpsRes/CokeSupplyChain/latexc6225364c4b2df199eec362b876b546b.png)

