Case Study: The American Steel Transshipment Problem
Submitted: 15 Feb 2008
Application Areas: Logistics
Contents
Problem Description
American Steel, an Ohio-based steel manufacturing company, produces steel at its two steel mills located at Youngstown and Pittsburgh. The company distributes finished steel to its retail customers through the distribution network of regional and field warehouses shown below:
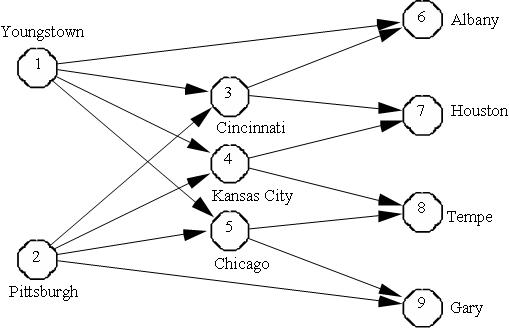
The network represents shipment of finished steel from American Steel's two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
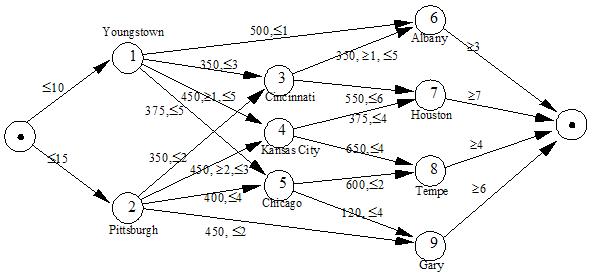
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the
cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
| From node |
To node |
Cost |
Minimum |
Maximum |
| Youngstown |
Albany |
500 |
- |
1000 |
| Youngstown |
Cincinnati |
350 |
- |
3000 |
| Youngstown |
Kansas City |
450 |
1000 |
5000 |
| Youngstown |
Chicago |
375 |
- |
5000 |
| Pittsburgh |
Cincinnati |
350 |
- |
2000 |
| Pittsburgh |
Kansas City |
450 |
2000 |
3000 |
| Pittsburgh |
Chicago |
400 |
- |
4000 |
| Pittsburgh |
Gary |
450 |
- |
2000 |
| Cincinnati |
Albany |
350 |
1000 |
5000 |
| Cincinnati |
Houston |
550 |
- |
6000 |
| Kansas City |
Houston |
375 |
- |
4000 |
| Kansas City |
Tempe |
650 |
- |
4000 |
| Chicago |
Tempe |
600 |
- |
2000 |
| Chicago |
Gary |
120 |
- |
4000 |
The current monthly demand at American Steel's four field warehouses is as follows:
| Field Warehouses |
Monthly Demand |
| Albany, N.Y. |
3000 |
| Houston |
7000 |
| Tempe |
4000 |
| Gary |
6000 |
The Youngstown and Pittsburgh mills can produce up to 10,000 tons and 15,000 tons of steel per month, respectively. The management wants to know the least cost monthly shipment plan.
Return to top
Problem Formulation
The American Steel Problem can be solved as a transshipment problem. The supply at the supply nodes is the maximum production at the steel mills, i.e., 10,000 and 15,000 for Youngstown and Pittsburgh repsectively. The demand at demand nodes in given by the demand at the field warehouses and the other nodes are transshipment nodes. The costs and bounds on flow through the network are also given. The most compact formulation for this problem is a network formulation (see
The Transshipment Problem for details).
 Return to top
Return to top
Computational Model
We can use the AMPL model file
transshipment.mod (see
The Transshipment Problem in AMPL for details) to solve the American Steel Transshipment Problem. We need a data file to describe the nodes, arcs, costs and bounds. The node set is simply a list of the node names:
set NODES := Youngstown Pittsburgh
Cincinnati 'Kansas City' Chicago
Albany Houston Tempe Gary ;
Note that
Kansas City must be enclosed in
' and
' because of the whitespace in the name.
The arc set is 2-dimensional and can be
defined in a number of different ways:
# List of arcs
set ARCS := (Youngstown, Albany), (Youngstown, Cincinnati), ... , (Chicago, Gary) ;
# Table of arcs
set ARCS: Cincinnati 'Kansas City' Chicago Albany Houston Tempe Gary :=
Youngstown + + + + - - -
Pittsburgh + + + - - - +
.
.
.
# Array of arcs
set ARCS :=
(Youngstown, *) Cincinnati 'Kansas City' Chicago Albany
(Pittsburgh, *) Cincinnati 'Kansas City' Chicago Gary
.
.
.
(Chicago, *) Tempe Gary
;
Since the node set is small and the arc set is "dense", i.e., many of the node pairs are represented in the arc set, we choose a
table to define ARCS:
set ARCS: Cincinnati 'Kansas City' Chicago Albany Houston Tempe Gary :=
Youngstown + + + + - - -
Pittsburgh + + + - - - +
Cincinnati - - - + + - -
'Kansas City' - - - - + + -
Chicago - - - - - + + ;
The
NetDemand can be defined easily from the supply and demand. Since the default is 0 we don't need to define
NetDemand for the transshipment nodes:
param NetDemand :=
Youngstown 10000
Pittsburgh 15000
Albany 3000
Houston 7000
Tempe 4000
Gary 6000
;
We can use
lists, tables or arrays to define the parameters for the American Steel Transhippment Problem,
but in this case we will use a list and
define multiple parameters at once. This allows us to "cut-and-paste" the parameters from the problem description. Note the use of
. for parameters where the defaults will suffice (e.g.,
Lower for
Youngstown and
Albany):
param: Cost Lower Upper:=
Youngstown Albany 500 . 1000
Youngstown Cincinnati 350 . 3000
Youngstown 'Kansas City' 450 1000 5000
Youngstown Chicago 375 . 5000
Pittsburgh Cincinnati 350 . 2000
Pittsburgh 'Kansas City' 450 2000 3000
Pittsburgh Chicago 400 . 4000
Pittsburgh Gary 450 . 2000
Cincinnati Albany 350 1000 5000
Cincinnati Houston 550 . 6000
'Kansas City' Houston 375 . 4000
'Kansas City' Tempe 650 . 4000
Chicago Tempe 600 . 2000
Chicago Gary 120 . 4000
;
Note that the cost is in $/1000 ton, so we must divide the cost by 1000 in our script file before solving:
reset;
model transshipment.mod;
data steel.dat;
let {(m, n) in ARCS} Cost[m, n] := Cost[m, n] / 1000;
option solver cplex;
solve;
display Flow;
Return to top
Results
Implementing the usual script file with
transshipment.mod and
steel.dat (with the
Cost modification) gives us the optimal
Flow variables:
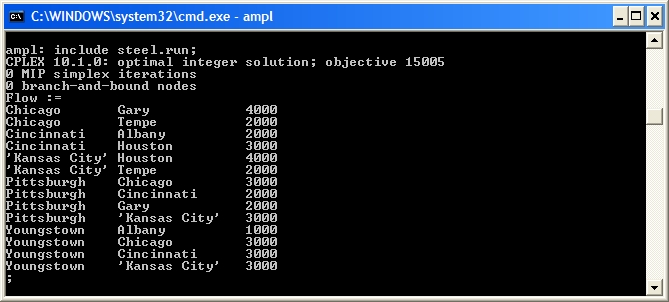
If the total supply is greater than the total demand, the transshipment problem will solve, but flow may be left in the network (in this case at the Pittsburgh node). If total supply is less than demand, then the problem becomes infeasible! Even in the case of infeasibility, it is preferable to solve the transshipment problem using a dummy supply node so that we can analyse where there is a shortfall in demand. We can balance the problem by either adding a dummy supply node with arcs to all the demand nodes or adding a dummy demand node with arcs from all the supply nodes:
balance_transshipment.mod
# The following parameters are needed to use balance_transshipment.run
param difference;
param dummyDemandCost {NODES};
param dummySupplyCost {NODES};
balance_transshipment.run
let difference := (sum {s in NODES} Supply[s])
- (sum {d in NODES} Demand[d]);
let NODES := NODES union {'Dummy'};
if difference > 0 then
{
print "Total Supply > Total Demand";
print "Solving with dummy supply node...";
let Demand['Dummy'] := difference;
for {n in NODES : Supply[n] > 0} {
let ARCS := ARCS union {(n, 'Dummy')};
let Cost[n, 'Dummy'] := dummyDemandCost[n];
}
}
else if difference < 0 then
{
print "WARNING: Total Supply < Total Demand, problem is infeasible!";
print "Solving with dummy demand node...";
let Demand['Dummy'] := - difference;
for {n in NODES : Demand[n] > 0} {
let ARCS := ARCS union {('Dummy', n)};
let Cost['Dummy', n] := dummySupplyCost[n];
}
}; # else the problem is balanced
steel.run
# steel.run
#
# Written by Mike O'Sullivan & Cameron Walker 2004
#
# This file contains a script for sensitivity analysis
# of the American Steel transshipment model.
#
# Last modified: 27/2/2004
reset;
model transshipment.mod;
model balance_transshipment.mod;
data steel.dat;
let {(m, n) in ARCS} Cost[m, n] := Cost[m, n] / 1000;
for {n in NODES} {
let dummyDemandCost[n] := 0;
let dummySupplyCost[n] := 0;
}
include balance_transshipment.run;
option solver cplex;
solve;
display Flow;
Note We also add a
???LINK??? check statement to our model file to ensure the problem is balanced:
check : sum {n in NODES} Supply[n] = sum {n in NODES} Demand[n];
Our solution now shows that there is 5000 ton of steel remaining at the Pittsburgh Mill, i.e., the flow from
Pittsburgh to
Dummy is 5000.
POST-OPTIMAL ANALYSIS
Validation
For our solution to be valid we need it to be integer. Observing the
Flow values shows that it is in fact integer. Moreover, no branch-and-bound nodes were required to make it integer. The transshipment problem is also naturally integer (like the transportation problem), so solving it as a linear programme will give integer solutions. In fact,
any network flow problem with integer supplies, demands and arc capacities has naturally integer solutions.
Parametric Analysis
If
???LINK??? sensitivity analysis shows that improvements to the objective
function may be achieved by changing problem data, then we may use
???LINK??? parametric analysis to see the effect of these changes.
.
.
.
include balance_transshipment.run;
option presolve 0;
option solver cplex;
option cplex_options 'presolve 0 sensitivity';
solve;
display Flow;
display _varname, _var.down, _var.current, _var.up, _var.rc;
display _conname, _con.down, _con.current, _con.up, _con.dual;

The sensitivity analysis shows that the solution is very sensitive to any changes in the constraint right-hand sides, with one exception
ConserverFlow at
Pittsburgh. However, we have variables on both sides of our constraints so we should
expand our constraints to see what the right-hand side is:

For the supply nodes the right-hand side is the negative of the supply, for the demand nodes the right-hand side is the demand and for the transshipment nodes the right-hand side is 0. Thus, any changes we make to the supply or demand at the nodes will affect our optimal solution. The only exception is that the right-hand side of the
ConserveFlow['Pittsburgh'] can decrease without affecting our solution. Since
Pittsburgh is a supply node (so the right-hand side is the negative of the supply) this means we can increase the supply at Pittsburgh without affecting our solution. This makes sense as Pittsburgh already has excess supply.
However, it seems like we can improve our objective the most by decreasing the demand at Tempe (the shadow price is 1.125), but the Allowable Minimum is such that we cannot discern what the change will be (the solution will change immediately). We can see the effect by using an
???LINK??? AMPL loop :
.
.
.
display TotalCost;
set CHANGES;
param Objective {CHANGES};
param OldDemand;
let OldDemand := Demand['Tempe'];
let CHANGES := {100..1000 by 100};
for {i in CHANGES} {
let Demand['Tempe'] := OldDemand - i;
display Demand['Tempe'];
# Rebalance the problem
include balance_transshipment.run;
solve;
let Objective[i] := TotalCost;
}

Note that we had to alter
balance_transshipment.run to consider problems that have been balanced previously:
balance_transshipment.run
let difference := (sum {s in NODES : s <> 'Dummy'} Supply[s])
- (sum {d in NODES : d <> 'Dummy'} Demand[d]);
if 'Dummy' not in NODES then
let NODES := NODES union {'Dummy'};
if difference > 0 then
{
print "Total Supply > Total Demand";
print "Solving with dummy supply node...";
let Demand['Dummy'] := difference;
for {n in NODES : Supply[n] > 0} {
let ARCS := ARCS union {(n, 'Dummy')};
let Cost[n, 'Dummy'] := dummyDemandCost[n];
}
}
else if difference < 0 then
{
print "WARNING: Total Supply < Total Demand, problem is infeasible!";
print "Solving with dummy demand node...";
let Demand['Dummy'] := - difference;
for {n in NODES : Demand[n] > 0} {
let ARCS := ARCS union {('Dummy', n)};
let Cost['Dummy', n] := dummySupplyCost[n];
}
}; # else the problem is balanced
The AMPL parametric analysis shows that, by decreasing the demand for steel at Tempe, we can get a consistent reduction in our objective function, even though this was not clear from our initial sensitivity analysis.
When we consider the sensitvity analysis for variable costs, we see that the only costs that affect our solution are the transportation costs from Pittsburgh and Youngstown to Chicago (all the other costs have Allowable Min and Allowable Max such that no "sensible" change would have any effect). Suppose American Steel are negotiating a new contract with the shipping company that takes their steel from Pittsburgh to Chicago. They estimate that they can get a reduction of around \$25/1000 ton of steel (taking the price from \$400/1000 ton to \$375/1000 ton), but want to know if they should negotiate for a lower price. The sensitivity analysis shows that below \$375/1000 ton the solution will change, so let's use parametric analysis to see what happens:
.
.
.
display TotalCost;
set CHANGES;
param Objective {CHANGES};
param OldCost;
let OldCost := Cost['Pittsburgh', 'Chicago'];
let CHANGES := {0..0.05 by 0.005};
for {i in CHANGES} {
let Cost['Pittsburgh', 'Chicago'] := OldCost - i;
display Cost['Pittsburgh', 'Chicago'];
# Rebalance the problem
include balance_transshipment.run;
solve;
let Objective[i] := TotalCost;
}
The parametric analysis shows that the objective function decreases at a greater rate if the price drops below $375/1000 ton, so American Steel should try and negotiate the price down even further.
 Return to top
Return to top
Conclusions
There is quite a bit of information to summarise and many ways to present it. Some suggestions include:
- Summarise the problem as usual and list the shipments that American Steel should make (similar to the transportation problem);
- Summarise the problem as usual and present a table of shipments that American Steel should make;
- Draw the network formulation for the problem (being sure to specify what the labels mean). Then draw the actual solution on top of the network formulation. You could colour code flows long arcs to show if they are at their bounds.
Implementation and Ongoing Monitoring
Given that the solution is very sensitive to the supply and demand amounts, careful consideration of the accuracy of these figures is important. Making sure that the bounds on the arcs are reliable is another concern.
Ongoing monitoring of the supply, demand and bounds will help American Steel to keep making good decisions. As shown in the parametric analysis, ongoing negotiation of transportation prices along important routes will help American Steel reduce their expenditure.
Return to top
Extra for Experts
Another common network flow problem that uses almost the same model as transshipment is the
maximum flow problem. The objective of this problem is to maximise flow through the network. The only changes to
transshipment.mod are:
- A new variable
FlowOut is introduced at each node;
-
FlowOut has lower and upper bounds, often the upper bound is set to as the Demand at the nodes;
-
FlowOut replaces Demand in the ConserveFlow constraints;
- The
ConserveFlow constraint becomes an equality constraint as all flow must be accounted for (no storage at the nodes);
-
Cost of transshipment is ignored;
- The objective is to maximise the total flow out of the network
sum {n in NODES} FlowOut[n];
- The problem no longer needs to be balanced.
Maxflow.mod
???ATTACH MAXFLOW.MOD HERE???
If we set
MaxOut to
Demand for all nodes:
let {n in NODES} MaxOut[n] := Demand[n];
then we see that currently all the demands are being met via the American Steel distribution network (the total flow out = the total demand):
 Return to top
Return to top
Student Tasks
- Solve The American Steel Problem. Write a management summary of your solution.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- American Steel are planning a marketing campaign to increase demand in their four markets Albany, Tempe, Houston and Gary. However, they would like to know the maximum demand their distribution network can handle (in each market) before they proceed. Write a script file that uses
maxflow.mod and steel.dat to find the maximum demand they can supply in each market.
What to hand in Hand in your script file and a management summary of your solution.
Return to top
 The network represents shipment of finished steel from American Steel's two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
The network represents shipment of finished steel from American Steel's two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
 Return to top
Return to top
 If the total supply is greater than the total demand, the transshipment problem will solve, but flow may be left in the network (in this case at the Pittsburgh node). If total supply is less than demand, then the problem becomes infeasible! Even in the case of infeasibility, it is preferable to solve the transshipment problem using a dummy supply node so that we can analyse where there is a shortfall in demand. We can balance the problem by either adding a dummy supply node with arcs to all the demand nodes or adding a dummy demand node with arcs from all the supply nodes:
balance_transshipment.mod
If the total supply is greater than the total demand, the transshipment problem will solve, but flow may be left in the network (in this case at the Pittsburgh node). If total supply is less than demand, then the problem becomes infeasible! Even in the case of infeasibility, it is preferable to solve the transshipment problem using a dummy supply node so that we can analyse where there is a shortfall in demand. We can balance the problem by either adding a dummy supply node with arcs to all the demand nodes or adding a dummy demand node with arcs from all the supply nodes:
balance_transshipment.mod
 The sensitivity analysis shows that the solution is very sensitive to any changes in the constraint right-hand sides, with one exception
The sensitivity analysis shows that the solution is very sensitive to any changes in the constraint right-hand sides, with one exception  For the supply nodes the right-hand side is the negative of the supply, for the demand nodes the right-hand side is the demand and for the transshipment nodes the right-hand side is 0. Thus, any changes we make to the supply or demand at the nodes will affect our optimal solution. The only exception is that the right-hand side of the
For the supply nodes the right-hand side is the negative of the supply, for the demand nodes the right-hand side is the demand and for the transshipment nodes the right-hand side is 0. Thus, any changes we make to the supply or demand at the nodes will affect our optimal solution. The only exception is that the right-hand side of the  Note that we had to alter
Note that we had to alter  Return to top
Return to top
 Return to top
Return to top



