Case Study: The American Steel Transshipment Problem

Submitted: 15 Feb 2008

Operations Research Topics: LinearProgramming, IntegerProgramming, NetworkOptimisation, TransshipmentProblem

Application Areas: Logistics

Contents

• Problem Description
• Problem Formulation
• Computational Model
• Results
• Conclusions
• StudentTasks

Problem Description

American Steel, an Ohio-based steel manufacturing company, produces steel at its two steel mills located at Youngstown and Pittsburgh. The company distributes finished steel to its retail customers through the distribution network of regional and field warehouses shown below: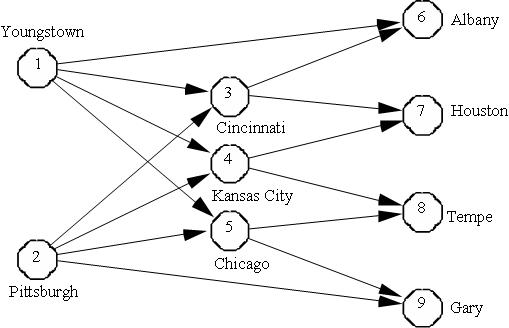

The network represents shipment of finished steel from American Steel's two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.

Table 1 presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more than 5000 tons/month due the shortage of rail cars.

Table 1 Arc Costs and Limits

The current monthly demand at American Steel's four field warehouses is shown in Table 2.

Table 2 Monthly Demands

The Youngstown and Pittsburgh mills can produce up to 10,000 tons and 15,000 tons of steel per month, respectively. The management wants to know the least cost monthly shipment plan.

Return to top

Problem Formulation

The American Steel Problem can be solved as a transshipment problem. The supply at the supply nodes is the maximum production at the steel mills, i.e., 10,000 and 15,000 for Youngstown and Pittsburgh respectively. The demand at demand nodes in given by the demand at the field warehouses and the other nodes are transshipment nodes. The costs and bounds on flow through the network are also given. The most compact formulation for this problem is a network formulation (see The Transshipment Problem for details).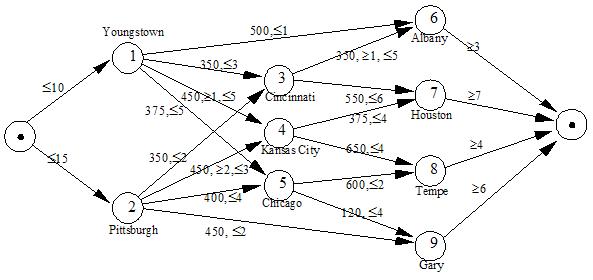

Return to top

Computational Model

set NODES := Youngstown  Pittsburgh
             Cincinnati 'Kansas City' Chicago
             Albany      Houston      Tempe   Gary ;

# List of arcs
set ARCS := (Youngstown, Albany), (Youngstown, Cincinnati), ... , (Chicago, Gary) ;

# Table of arcs
set ARCS:   Cincinnati 'Kansas City' Chicago Albany Houston Tempe Gary :=
Youngstown         +          +         +      +       -      -    -
Pittsburgh         +          +         +      -       -      -    +
.
.
.

# Array of arcs
set ARCS :=
(Youngstown, *)    Cincinnati 'Kansas City' Chicago Albany
(Pittsburgh, *)    Cincinnati 'Kansas City' Chicago Gary
.
.
.
(Chicago, *)       Tempe       Gary
 ;

set ARCS:   Cincinnati 'Kansas City' Chicago Albany Houston Tempe Gary :=
Youngstown         +          +         +      +       -      -    -
Pittsburgh         +          +         +      -       -      -    +
Cincinnati         -          -         -      +       +      -    -
'Kansas City'      -          -         -      -       +      +    -
Chicago            -          -         -      -       -      +    + ;

param      NetDemand :=
Youngstown -10000
Pittsburgh -15000
Albany       3000
Houston      7000
Tempe        4000
Gary         6000
 ;

param:                  	Cost    Lower  	Upper:=
Youngstown	Albany		500	.	1000
Youngstown	Cincinnati	350	.	3000
Youngstown	'Kansas City'	450	1000	5000
Youngstown	Chicago		375	.	5000
.
.
.
Chicago		Gary		120	.	4000
 ;

reset;

model transshipment.mod;

data steel.dat;

let {(m, n) in ARCS} Cost[m, n] := Cost[m, n] / 1000;

option solver cplex;
solve;

display Flow;

Return to top

Results

Using transshipment.mod, and the data and script files defined in Computational Model we can solve the American Steel Transshipment Problem to get the optimal Flow variables:

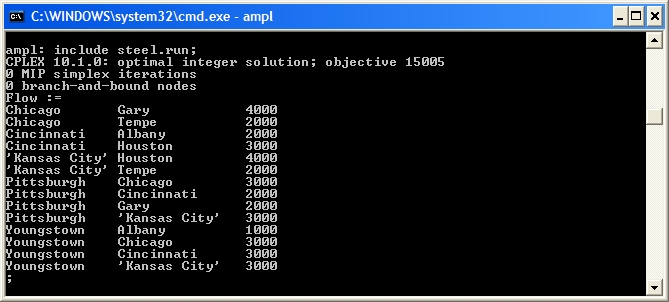If the total supply is greater than the total demand, the transshipment problem will solve, but flow may be left in the network (in this case at the Pittsburgh node). In transshipment.mod we check that sum {n in NODES} NetDemand[n] <= 0 to ensure a problem is feasible before solving.

If total supply is less than demand (hence the problem is infeasible) we can add a dummy supply node (see with arcs to all the demand nodes. The optimal solution will show the "best" nodes to send the extra supply to.

Return to top

Conclusions

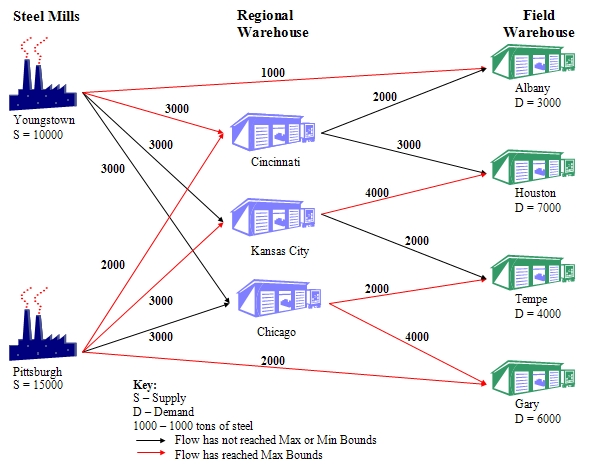
In order to minimise the monthly shipment costs, American Steel should follow the shipment plan shown in Table 3.

Table 3 Optimal Shipment Plan

As with many network problems, it can be illuminating to display the solution graphically as shown in Figure 1.

Figure 1 Optimal Shipment Plan

Return to top

Student Tasks

1. Solve the American Steel Transshipment Problem. Write a management summary of your solution.

   What to hand in Hand in your management summary.

Return to top