Case Study: The Surfboard Production Problem
Submitted: 8 Feb 2008
Operations Research Topics: NonlinearProgramming
Application Areas: Sports Equipment Manufacturing
Contents
- Problem Description
- Problem Formulation
- Computational Model
- Results
- Conclusions
- Extra for Experts
- StudentTasks
Problem Description
A surfboard manufacturer is planning his monthly surfboard production of Malibu and Super Thruster boards. He has limitations on his supply of fibreglass resin, having only 72 kilos left in stock. To construct a Malibu board requires 3 kilos of resin, and to build a Super Thruster one needs 4 kilos. He has consulted a market research firm about the effect of the price he charges on the demand for the surfboards. They have provided him with the following information. If the price of a Malibu board isProblem Formulation
To formulate this problem we will use the 4 steps for formulating a mathematical programme. 1. Identify the Decision Variables
The manufacturer has two decisions to make: 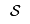 and then define the decision variables:
and then define the decision variables:
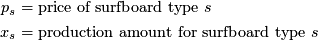
2. Formulate the Objective Function
- the price to charge for the surfboards;
- how many surfboards to make.
The manufacturer wants to maximise his return from selling the surfboards. He does not want to have any left over as that is a waste of resin, so he will not make enough boards to satisfy demand. Thus, he assumes he will sell all the boards he makes. His return will be the number of boards of each type he makes multiplied by the price he chooses for that type of board:
![\[ \max \sum_{s \in {\cal S}} p_s x_s \]](/pub/OpsRes/SurfboardProduction/latexc41c7da6f78bfc28be35de8f67f01606.png)
3. Formulate the Constraints
The manufacturer only has 72 kilograms of resin to make his boards. Define a set of raw materials  and
and 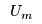 as the upper limit of each raw material available (for this example
as the upper limit of each raw material available (for this example  and
and 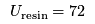 . Also, define
. Also, define 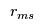 as the amount of raw material
as the amount of raw material 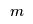 required (in kg) to make a surfboard of type
required (in kg) to make a surfboard of type 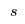 . The manufacturing constraints are:
. The manufacturing constraints are:
![\[ \sum_{s \in {\cal S}} r_{ms} x_s \leq U_m, m \in {\cal M} \]](/pub/OpsRes/SurfboardProduction/latex4ea8996f76e90f290147a4f36d7b0b3b.png) For this example
For this example
![\[ 4 x_\text{Malibu} + 3 x_\text{Super Thruster} \leq 72 \]](/pub/OpsRes/SurfboardProduction/latexe4728e2214b6a383eb1fa5b52fca7d5d.png) for resin.
Furthermore, he does not believe he will sell more than the estimated demand, i.e.,
for resin.
Furthermore, he does not believe he will sell more than the estimated demand, i.e., 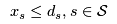 , where
, where 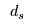 is defined by the market research equations. Thus, he won't make more than those estimates.
Finally, he cannot sell a negative number of boards, i.e.,
is defined by the market research equations. Thus, he won't make more than those estimates.
Finally, he cannot sell a negative number of boards, i.e., 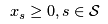 and he can only sell an integer number of boards, i.e.,
and he can only sell an integer number of boards, i.e.,  .
.
The complete formulation is:
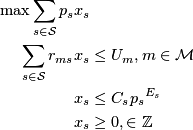
Computational Model
To build our mathematical programme in AMPL we first define the sets for surfboardsset SURFBOARDS; set MATERIALS;Next, we add the parameters for surfboards
surfboard.mod:
param Coefficient {SURFBOARDS};
param Exponent {SURFBOARDS};
As well as the parameters for raw materials:
param Supply {MATERIALS};
and for the surfboard "recipe"
param Recipe {MATERIALS, SURFBOARDS};
Our final step, before implementing our formulation in surfboard.mod is to define the decision variables:
var Price {SURFBOARDS};
var Production {SURFBOARDS} >= 0, integer;
Now the formulation is straightforward:
maximize TotalProfit:
sum {s in SURFBOARDS} Price[s] * Production[s];
subject to MaterialSupply {m in MATERIALS} :
sum {s in SURFBOARDS} Recipe[m, s] * Production[s] <= Supply[m];
subject to SurfboardDemand {s in SURFBOARDS} :
Production[s] <= Coefficient[s] * (Price[s] ^ Exponent[s]);
Note Both the objective and the SurfboardDemand are nonlinear expressions.
The formulation data is specified in surfboard.dat. The sets are straightforward (note the use of ' to define the whitespace in Super Thruster):
set SURFBOARDS := Malibu 'Super Thruster' ; set MATERIALS := Resin ;and by defining multiple parameters at once we can define the demand equation parameters at the same time:
param: Coefficient Exponent := Malibu 12000 -1.5 'Super Thruster' 12000 -1.8 ;Using a list to define the
Supply parameter and a table to define the Recipe parameter completes surfboard.dat:
param Supply :=
Resin 72 ;
param Recipe :
Malibu 'Super Thruster' :=
Resin 3 4 ;
Since our mathematical programme is a nonlinear programme we cannot use CPLEX to solve our problem. In (the Student Edition) of AMPL we can use MINOS for nonlinear programming. The script file for solving this problem would typically be similar to:
reset; model surfboard.mod; data surfboard.dat; option solver minos; solve; display Price, Production;However, if you run this script file you will observe the following error:
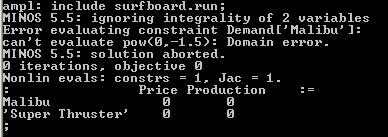 This error occurs because the initial values for
This error occurs because the initial values for Price (and Production) are set to 0. Both demand estimation functions have negative exponents, so are undefined for a value of 0, i.e.,
Price variables to be non-zero:
let Price['Malibu'] := 1; let Price['Super Thruster'] := 1;and resolve:
 Note that MINOS does not actually solve for integer variables:
Note that MINOS does not actually solve for integer variables:
MINOS 5.5: ignoring integrality of 2 variablesbut both the
Production variables both have integer values.
MINOS also terminated before determining optimality
MINOS 5.5: too many major iterations.By default, the number of major iterations allowed by MINOS is 50. If you increase the number of major iterations by changing the MINOS options:
option minos_options 'major_iterations=100';and resolve you will notice that the price of the Super Thruster board is slowly increasing, as is the total return. By increasing the limit on the major iterations to 1500 we get the optimal solution:
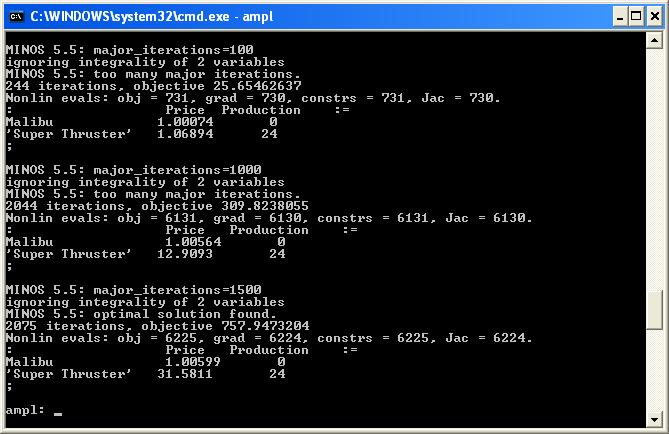 Return to top
Return to top
Results
Our computational model shows that the optimal solution is to produce 24 Super Thruster boards and sell them for $31.5811 each. Note that this solution yields integer production values, but the optimal prices ($31.958 for the Super Thruster boards and $1.01 for the Malibu boards) seem low. We may have encountered a local optimum. If the manufacturer only makes Malibu boards he has enough resin to make 18 boards. To get demand for 18 boards his price This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS server
This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS serversurfboard.mod and surfboard.dat as the model and data files and revise our script file
let Price['Malibu'] := 101.27; let Price['Super Thruster'] := 56.96; solve; display Price, Production;to solve using MINLP (on the NEOS Server) and find an optimal integer solution.
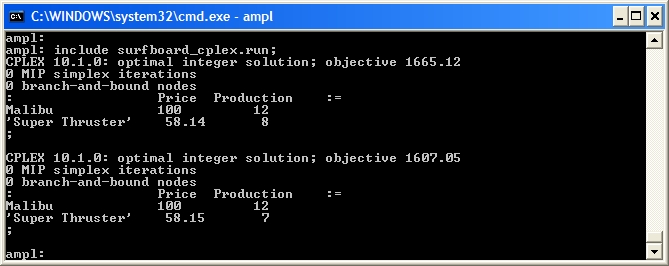
You are using the solver minlp. Executing AMPL. processing data. processing commands. 4 variables, all nonlinear 3 constraints; 6 nonzeros 2 nonlinear constraints 1 linear constraint 1 nonlinear objective; 4 nonzeros. MINLP-B&B (20020703): m(before SOS) = 3 m(a f t e r SOS) = 3 Optimal solution found 3 subproblems, objective = 1665.141545 Evals: obj = 107, constr = 107, grad = 46, Hes = 45 : Price Production := Malibu 100 12 'Super Thruster' 58.1427 8 ;The manufacturer will most likely want a price that is to the nearest cent. It is dangerous to round mathematical programme solutions as even a small change in the variable value may result in a large change in the objective function or may even cause the solution to become infeasible. Since the
Price variables cause our mathematical programme to be nonlinear, we will fix these variables and use CPLEX to solve for the Production variables:
reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.15; fix Price; solve; display Price, Production;Note that we rounded both up and down to check the "local neighbourhood" of the optimal point (see some discussion about solution accuracy
 Return to top
Return to top
Conclusions
The Surfboard Production problem is a relatively simple problem to formulate, but its solution requires careful thought and analysis. The management summary surfboard.doc contains some information about the initial values used (so future consultants/researchers can follow the work) and details about the NEOS Optimization ServerExtra for Experts
Examining the Objective Function
The nonlinearity in this problem is introduced by the price variables. If these variables are fixed we can use CPLEX to find the optimal production levels. By looping over possible pairs of values for the prices and solving for the production levels we can build up a picture of the objective function.
param Objective {1..150, 1..150};
fix Price;
for {p in 1..150 by 1, q in 1..150 by 1} {
let Price['Malibu'] := p;
let Price['Super Thruster'] := q;
option solver cplex;
solve;
let Objective[p, q] := TotalProfit;
}
Using this picture we can try to discern if the optimal solution we found using MINLP (shown below) is the global optimum.
: Price Production := Malibu 100 12 'Super Thruster' 58.1427 8Hint This
for loop may take a long time to finish. Also, you may want to print the TotalProfit parameter to a file using AMPL.
Return to top
Student Tasks
- Try different initial values for both
PriceandProduction. Do you believe that the MINLP solution is the global optimum? What to hand in Hand in a summary of your different experiments along with an answer to the global optimality question. Be sure to justify your answer. - Experts Only Use AMPL and CPLEX to create a picture of the objective function. Does the solution we found using MINLP look like the global optimum? What to hand in Your picture of the objective function. Your answer to the global optimality questions. Be sure to justify your answer.
| I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
surfboard.dat | r1 | manage | 0.3 K | 2008-03-18 - 10:24 | TWikiAdminUser | |
| |
surfboard.doc | r2 r1 | manage | 26.0 K | 2009-10-09 - 01:19 | MichaelOSullivan | |
| |
surfboard.mod | r2 r1 | manage | 1.0 K | 2008-03-18 - 20:58 | MichaelOSullivan | |
| |
surfboard.run | r1 | manage | 0.4 K | 2008-03-18 - 10:24 | TWikiAdminUser |
This topic: OpsRes > SubmitCaseStudy > SurfboardProduction
Topic revision: r29 - 2018-11-23 - TWikiAdminUser
Ideas, requests, problems regarding TWiki? Send feedback

