Supply Chain Mathematical Programmes
This material is a summary of the material on supply chain networks from
Chapter 2 Supply Chain Networks in
Supply Chain Network Economics: Dynamics of Prices, Flows and Profits by
Anna Nagurney (2006).
Supply Chains
- Introduction
- The Manufacturer's Problem
- The Retailer's Problem
- The Consumer's Problem
- Equilibrium and Variational Inequalities
Introduction
Throughout a supply chain there are many organisations who are trying to make the best decision for their business. These decisions can be formulated as
mathematical programmes. We will introduce a supply chain model that is a simplification of that presented in the
Supply Chains introduction. We will formulate the mathematical programmes faced by the organisations at each stage of this supply chain. This simplification can be easily extended to supply chain models with more stages (e.g., see
Supply Chains) by inserting more
Retailer's Problems into the simplified model.
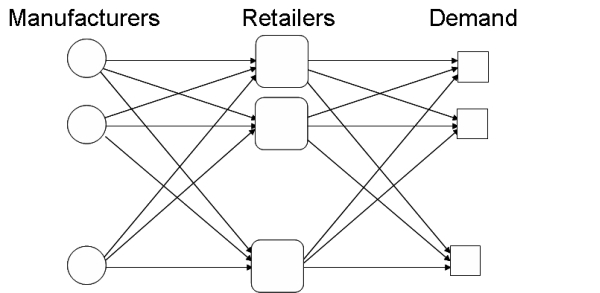
The supply chain model considered here has three stages (shown in
Figure 1):
- The manufacturers;
- The retailers;
- The demand markets. Products are created by the manufacturers, sold to the retailers where they are stored, distributed, etc and then sold again in the demand markets to consumers.
Figure 1 A 3-stage supply chain model (adapted from
Supply Chain Network Economics
)
The rest of this topic deals with the mathematical programmes faced by the manufacturers, retailers and consumers (in the demand markets).
Return to top
The Manufacturer's Problem
Each manufacturer
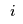
(from the set of manufacturers
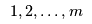
must determine an optimal output quantity
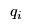
which is split into flows
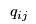
to send to each retailer
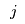
(from the set of retailers
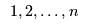
). Of course all output is sent to retailers so
The production cost
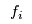
for manufacturer
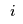
may be influenced not only by their output
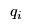
, but also by the outputs from other manufacturers, e.g., due the competition for shared resources. Thus,
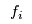
is a function of the
vector 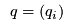
which may also be expressed as the matrix of flows from manufacturers to retailers, i.e.,
so
Finally, there is a transaction cost
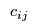
associated with sending flow
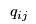
from manufacturer
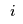
to retailer
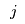
, i.e.,
Each manufacturer
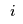
sets a unit price
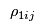
for selling their output to retailer
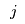
. Now manufacturer
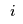
want to maximise their profit, i.e., total income - production cost - transaction cost, over the set of non-negative flows:
Return to top
The Retailer's Problem
Each retailer
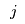
must determine their optimal flow
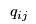
to receive from manufacturer
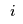
and also their optimal flow
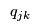
to sell to consumers in demand market
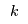
(in the set of demand markets
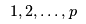
).
There is an associated handling cost
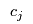
that may depend on the flow to other retailers, e.g., competition for output from the manufacturers:
Each retailer
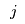
sets a unit price
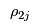
for sending flow to a demand market. Note that this price does not depend on the market (as consumers will simply move to the demand markets with the lowest price).
Now the retailer must choose flows to maximise their total profit (total income - handling cost - purchase cost):
Return to top
The Consumers' Problem
The consumers within a demand market
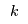
must determine how much of the incoming flow to purchase. They take the price
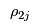
from each retailer and there is an associated
unit transaction cost
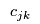
for purchasing flow from retailer
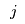
. This cost may depend on the behaviour of consumers in other demand markets, e.g., . competition for flows from retailers, i.e.,
and
The combination of the different prices and unit transaction costs gives rise to an "effective" price
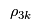
for a consumer to purchase a unit of flow in demand market
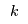
.
The demand for flow in demand market
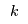
is determined by the demand curve, a function of the effective price, i.e.,
The consumers within demand market
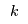
choose flows to minimise their total cost while meeting demand:
Return to top
Equilibrium and Variational Inequalities
If the prices
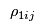
,
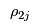
and
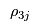
are not
coordinated then solving the
Manufacturer's Problem, the
Retailer's Problem and the
Consumers' Problem will give inconsistent values for
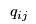
and
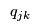
. That is, the manufacturers will want to ship different amounts to the retailers than the retailers will want to receive from the manufacturers and the retailers will want to sell different amounts to the demand markets from the amounts that the consumers at the demand markets want to purchase. However, these prices will adjust until the supply chain reaches
equilibrium and the flows from the different mathematical programmes agree.
One way to find this equilibrium point is to solve a
variational inequality
.
Theorem 1 gives the necessary variational inequalities:
Theorem 1: Variational Inequality The equilibrium state governing the supply chain model according to the optimality conditions of the supply chain mathematical programmes (1), (2) and (3) is equivalent to the solution of the variational inequality problem given by: determine the equilibrium vectors of product shipments, shadow prices, and demand market prices 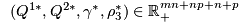 satisfying
satisfying
Once the equilibrium state has been found the manufacturers' prices and the retailers' prices can be calculated:
Return to top
--
MichaelOSullivan - 31 Mar 2008
Latex rendering error!! dvi file was not created.
 The rest of this topic deals with the mathematical programmes faced by the manufacturers, retailers and consumers (in the demand markets).
Return to top
The rest of this topic deals with the mathematical programmes faced by the manufacturers, retailers and consumers (in the demand markets).
Return to top
![\[ Q^1 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1n} \\ q_{21} & q_{22} & \cdots & q_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ q_{m1} & q_{m2} & \cdots & q_{mn} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexb682066036205339cf7d9bdcf6f1c0c2.png)


![\[ Q^2 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1p} \\ q_{21} & q_{22} & \cdots & q_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ q_{n1} & q_{n2} & \cdots & q_{np} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexd4ad75dc59dcc4e9ddbb8a8c79db2777.png)

![\begin{equation*} \begin{split} & \sum_{i=1}^m \sum_{j=1}^n \left[ \frac{\partial f_i(Q^{1*})}{\partial q_{ij}} + \frac{\partial c_{ij}(q_{ij}^*)}{\partial q_{ij}} + \frac{\partial c_j(Q^{1*})}{\partial q_{ij}} - \gamma_j^* \right] \times \left[ q_{ij} - q_{ij}^* \right] \ &+ \sum_{j=1}^n \sum_{k=1}^p \left[ c_{jk}(Q^{2*}) + \gamma_j^* - \rho_{3k}^* \right] \times \left[ q_{jk} - q_{jk}^* \right] \ &+ \sum_{j=1}^n \left[ \sum_{i=1}^m q_{ij}^* - \sum_{k=1}^p q_{jk}^* \right] \times \left[ \gamma_j - \gamma_j^* \right] \ &+ \sum_{k=1}^p \left[ \sum_{j=1}^n q_{jk}^* - d_k(\rho_3^*) \right] \times \left[ \rho_{3k} - \rho_{3k}^* \right] \geq 0, \forall (Q^{1}, Q^{2}, \gamma, \rho_{3}) \in \mathbb{R}_+^{mn+np+n+p} \end{split} \end{equation*}](/pub/OpsRes/SupplyChainMP/latexeb6a8b0778a72360520dc2a4ce9ac2f5.png)
![$\displaystyle \rho_{1ij}^* = \left[ \frac{\partial f_i(Q^{1*})}{\partial q_{ij}} + \frac{\partial c_{ij}(q_{ij}^*)}{\partial q_{ij}} \right]$](/pub/OpsRes/SupplyChainMP/latex331aa8a89ded7f80f180b178861898f6.png) if
if 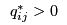 ;
;
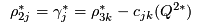 if
if 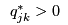 for some
for some 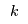 .
.

