| |
| META TOPICPARENT |
name="SupplyChains" |
<-- Ready to Review --> |
|
<
< | %BEGINLATEXPREAMBLE%
\usepackage{amsmath}
\usepackage{amssymb} |
>
> | %BEGINLATEXPREAMBLE% \usepackage{amsmath} \usepackage{amssymb} |
| | %ENDLATEXPREAMBLE%
Supply Chain Mathematical Programmes |
| |
Introduction |
|
<
< | Throughout a supply chain there are many organisations who are trying to make the best decision for their business. These decisions can be formulated as mathematical programmes. We will introduce a supply chain model that is a simplification of that presented in the Supply Chains introduction. We will formulate the mathematical programmes faced by the organisations at each stage of this supply chain. This simplification can be easily extended to supply chain models with more stages (e.g., see Supply Chains) by inserting more Retailer's Problems into the simplfied model. |
>
> | Throughout a supply chain there are many organisations who are trying to make the best decision for their business. These decisions can be formulated as mathematical programmes. We will introduce a supply chain model that is a simplification of that presented in the Supply Chains introduction. We will formulate the mathematical programmes faced by the organisations at each stage of this supply chain. This simplification can be easily extended to supply chain models with more stages (e.g., see Supply Chains) by inserting more Retailer's Problems into the simplified model. |
| |
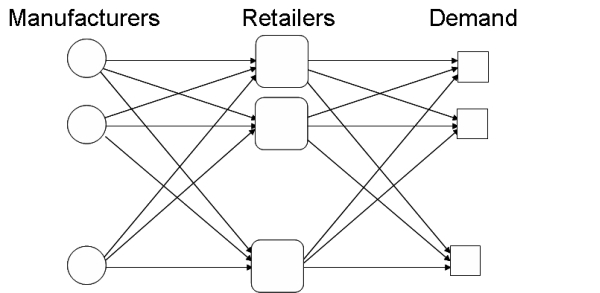
The supply chain model considered here has three stages (shown in Figure 1):
- The manufacturers;
|
|
<
< |
- The retailers;
- The demand markets.
Products are created by the manufacturers, sold to the retailers where they are stored, distributed, etc and then sold again in the demand markets to consumers. |
>
> |
- The retailers;
- The demand markets. Products are created by the manufacturers, sold to the retailers where they are stored, distributed, etc and then sold again in the demand markets to consumers.
|
| |
Figure 1 A 3-stage supply chain model (adapted from Supply Chain Network Economics ) ) |
|
<
< |  |
>
> |  |
| |
The rest of this topic deals with the mathematical programmes faced by the manufacturers, retailers and consumers (in the demand markets). |
| |
The Manufacturer's Problem |
|
<
< | Each manufacturer 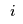 (from the set of manufacturers (from the set of manufacturers 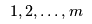 must determine an optimal output quantity must determine an optimal output quantity 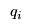 which is split into flows which is split into flows 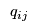 to send to each retailer to send to each retailer 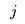 (from the set of retailers (from the set of retailers 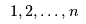 ). Of course all output is sent to retailers so ). Of course all output is sent to retailers so
|
>
> | Each manufacturer 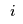 (from the set of manufacturers (from the set of manufacturers 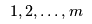 must determine an optimal output quantity must determine an optimal output quantity 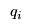 which is split into flows which is split into flows 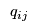 to send to each retailer to send to each retailer 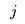 (from the set of retailers (from the set of retailers 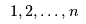 ). Of course all output is sent to retailers so ). Of course all output is sent to retailers so |
| | |
|
<
< | The production cost 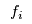 for manufacturer for manufacturer 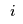 may be influenced not only by their output may be influenced not only by their output 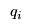 , but also by the outputs from other manufacturers, e.g., due the competition for shared resources. Thus, , but also by the outputs from other manufacturers, e.g., due the competition for shared resources. Thus, 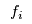 is a function of the vector is a function of the vector 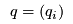 which may also be expressed as the matrix of flows from manufacturers to retailers, i.e.,
so
Finally, there is a transaction cost which may also be expressed as the matrix of flows from manufacturers to retailers, i.e.,
so
Finally, there is a transaction cost 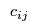 associated with sending flow associated with sending flow 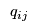 from manufacturer from manufacturer 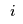 to retailer to retailer 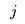 , i.e.,
Each manufacturer , i.e.,
Each manufacturer 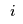 sets a unit price sets a unit price 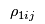 for selling their output to retailer for selling their output to retailer 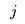 . Now manufacturer . Now manufacturer 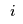 want to maximise their profit, i.e., total income - production cost - transaction cost, over the set of nonegative flows:
%BEGINLATEX{label="eq:manufacturer"}%
\begin{equation*}
\begin{array}{l@{ }l}
\displaystyle \max \sum_{j=1}^n \rho_{1ij} & \displaystyle q_{ij} - f_i(Q^1) - \sum_{j=1}^n c_{ij}(q_{ij}) \\text{subject to} \& q_{ij} \geq 0, j = 1, 2, \ldots, n
\end{array}
\end{equation*} want to maximise their profit, i.e., total income - production cost - transaction cost, over the set of nonegative flows:
%BEGINLATEX{label="eq:manufacturer"}%
\begin{equation*}
\begin{array}{l@{ }l}
\displaystyle \max \sum_{j=1}^n \rho_{1ij} & \displaystyle q_{ij} - f_i(Q^1) - \sum_{j=1}^n c_{ij}(q_{ij}) \\text{subject to} \& q_{ij} \geq 0, j = 1, 2, \ldots, n
\end{array}
\end{equation*} |
>
> | The production cost 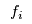 for manufacturer for manufacturer 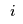 may be influenced not only by their output may be influenced not only by their output 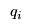 , but also by the outputs from other manufacturers, e.g., due the competition for shared resources. Thus, , but also by the outputs from other manufacturers, e.g., due the competition for shared resources. Thus, 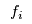 is a function of the vector is a function of the vector 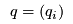 which may also be expressed as the matrix of flows from manufacturers to retailers, i.e., so
Finally, there is a transaction cost which may also be expressed as the matrix of flows from manufacturers to retailers, i.e., so
Finally, there is a transaction cost 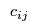 associated with sending flow associated with sending flow 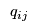 from manufacturer from manufacturer 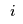 to retailer to retailer 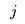 , i.e.,
Each manufacturer , i.e.,
Each manufacturer 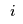 sets a unit price sets a unit price 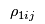 for selling their output to retailer for selling their output to retailer 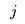 . Now manufacturer . Now manufacturer 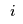 want to maximise their profit, i.e., total income - production cost - transaction cost, over the set of non-negative flows:
%BEGINLATEX{label="eq:manufacturer"}% \begin{equation*} \begin{array}{l@{ }l} \displaystyle \max \sum_{j=1}^n \rho_{1ij} & \displaystyle q_{ij} - f_i(Q^1) - \sum_{j=1}^n c_{ij}(q_{ij}) \ \text{subject to} \ & q_{ij} \geq 0, j = 1, 2, \ldots, n \end{array} \end{equation*} want to maximise their profit, i.e., total income - production cost - transaction cost, over the set of non-negative flows:
%BEGINLATEX{label="eq:manufacturer"}% \begin{equation*} \begin{array}{l@{ }l} \displaystyle \max \sum_{j=1}^n \rho_{1ij} & \displaystyle q_{ij} - f_i(Q^1) - \sum_{j=1}^n c_{ij}(q_{ij}) \ \text{subject to} \ & q_{ij} \geq 0, j = 1, 2, \ldots, n \end{array} \end{equation*} |
| | %ENDLATEX%
Return to top |
| |
Each retailer 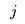 must determine their optimal flow must determine their optimal flow 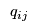 to receive from manufacturer to receive from manufacturer 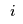 and also their optimal flow and also their optimal flow 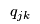 to sell to consumers in demand market to sell to consumers in demand market 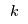 (in the set of demand markets (in the set of demand markets 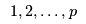 ). ). |
|
<
< | There is an associated handling cost 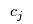 that may depend on the flow to other retailers, e.g., competition for output from the manufacturers: that may depend on the flow to other retailers, e.g., competition for output from the manufacturers:
|
>
> | There is an associated handling cost 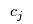 that may depend on the flow to other retailers, e.g., competition for output from the manufacturers: that may depend on the flow to other retailers, e.g., competition for output from the manufacturers: |
| |
Each retailer 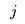 sets a unit price sets a unit price 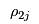 for sending flow to a demand market. Note that this price does not depend on the market (as consumers will simply move to the demand markets with the lowest price).
Now the retailer must choose flows to maximise their total profit (total income - handling cost - purchase cost): for sending flow to a demand market. Note that this price does not depend on the market (as consumers will simply move to the demand markets with the lowest price).
Now the retailer must choose flows to maximise their total profit (total income - handling cost - purchase cost): |
|
<
< | %BEGINLATEX{label="eq:retailer"}%
\begin{equation*}
\begin{array}{l@{ }l@{ }l}
\displaystyle \max \rho_{2j} \sum_{k=1}^p & q_{jk} & \displaystyle - \ c_j(Q^1) - \sum_{i=1}^m \rho_{1ij} q_{ij} \\text{subject to} \\displaystyle \hfill \sum_{k=1}^p & q_{jk} & \displaystyle \leq \sum_{i=1}^m q_{ij} \& q_{ij} &\geq 0, i = 1, 2, \ldots, m \& q_{jk} &\geq 0, k = 1, 2, \ldots, p
\end{array}
\end{equation*} |
>
> | %BEGINLATEX{label="eq:retailer"}% \begin{equation*} \begin{array}{l@{ }l@{ }l} \displaystyle \max \rho_{2j} \sum_{k=1}^p & q_{jk} & \displaystyle - \ c_j(Q^1) - \sum_{i=1}^m \rho_{1ij} q_{ij} \ \text{subject to} \ \displaystyle \hfill \sum_{k=1}^p & q_{jk} & \displaystyle \leq \sum_{i=1}^m q_{ij} \ & q_{ij} &\geq 0, i = 1, 2, \ldots, m \ & q_{jk} &\geq 0, k = 1, 2, \ldots, p \end{array} \end{equation*} |
| | %ENDLATEX%
Return to top
The Consumers' Problem |
|
<
< | The consumers within a demand market 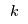 must determine how much of the incoming flow to purchase. They take the price must determine how much of the incoming flow to purchase. They take the price 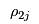 from each retailer and there is an associated unit transaction cost from each retailer and there is an associated unit transaction cost 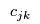 for purchasing flow from retailer for purchasing flow from retailer 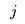 . This cost may depend on the behaviour of consumers in other demand markets, e.g., . competition for flows from retailers, i.e.,
and . This cost may depend on the behaviour of consumers in other demand markets, e.g., . competition for flows from retailers, i.e.,
and
|
>
> | The consumers within a demand market 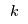 must determine how much of the incoming flow to purchase. They take the price must determine how much of the incoming flow to purchase. They take the price 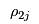 from each retailer and there is an associated unit transaction cost from each retailer and there is an associated unit transaction cost 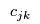 for purchasing flow from retailer for purchasing flow from retailer 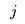 . This cost may depend on the behaviour of consumers in other demand markets, e.g., . competition for flows from retailers, i.e., and . This cost may depend on the behaviour of consumers in other demand markets, e.g., . competition for flows from retailers, i.e., and |
| |
The combination of the different prices and unit transaction costs gives rise to an "effective" price 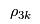 for a consumer to purchase a unit of flow in demand market for a consumer to purchase a unit of flow in demand market 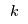 . . |
|
<
< | The demand for flow in demand market 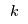 is determined by the demand curve, a function of the effective price, i.e., is determined by the demand curve, a function of the effective price, i.e.,
|
>
> | The demand for flow in demand market 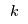 is determined by the demand curve, a function of the effective price, i.e., is determined by the demand curve, a function of the effective price, i.e., |
| |
The consumers within demand market 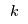 choose flows to minimise their total cost while meeting demand: choose flows to minimise their total cost while meeting demand: |
|
<
< | %BEGINLATEX{label="eq:consumer"}%
\begin{equation*}
\begin{array}{l@{ }l@{ }l}
\displaystyle \min \rho_{3k} \sum_{j=1}^n & q_{jk} \\text{subject to} \\displaystyle \hfill \sum_{j=1}^n & q_{jk} & \geq d_k(\rho_{3k}) \& q_{jk} &\geq 0, j = 1, 2, \ldots, n
\end{array}
\end{equation*} |
>
> | %BEGINLATEX{label="eq:consumer"}% \begin{equation*} \begin{array}{l@{ }l@{ }l} \displaystyle \min \rho_{3k} \sum_{j=1}^n & q_{jk} \ \text{subject to} \ \displaystyle \hfill \sum_{j=1}^n & q_{jk} & \geq d_k(\rho_{3k}) \ & q_{jk} &\geq 0, j = 1, 2, \ldots, n \end{array} \end{equation*} |
| | %ENDLATEX%
Return to top
Equilibrium and Variational Inequalities |
|
<
< | If the prices 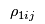 , , 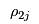 and and 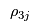 are not coordinated then solving the Manufacturer's Problem, the Retailer's Problem and the Consumers' Problem will give inconsistent values for are not coordinated then solving the Manufacturer's Problem, the Retailer's Problem and the Consumers' Problem will give inconsistent values for 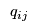 and and 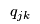 . That is, the manufacturers will want to ship different ammounts to the retailers than the retailers will want to receive from the maunfacturers and the retailers will want to sell different amounts to the demand markets from the amounts that the consumers at the demand markets want to purchase. However, these prices will adjust until the supply chain reaches equilibrium and the flows from the different mathematical programmes agree. . That is, the manufacturers will want to ship different ammounts to the retailers than the retailers will want to receive from the maunfacturers and the retailers will want to sell different amounts to the demand markets from the amounts that the consumers at the demand markets want to purchase. However, these prices will adjust until the supply chain reaches equilibrium and the flows from the different mathematical programmes agree. |
>
> | If the prices 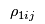 , , 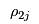 and and 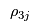 are not coordinated then solving the Manufacturer's Problem, the Retailer's Problem and the Consumers' Problem will give inconsistent values for are not coordinated then solving the Manufacturer's Problem, the Retailer's Problem and the Consumers' Problem will give inconsistent values for 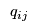 and and 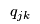 . That is, the manufacturers will want to ship different amounts to the retailers than the retailers will want to receive from the manufacturers and the retailers will want to sell different amounts to the demand markets from the amounts that the consumers at the demand markets want to purchase. However, these prices will adjust until the supply chain reaches equilibrium and the flows from the different mathematical programmes agree. . That is, the manufacturers will want to ship different amounts to the retailers than the retailers will want to receive from the manufacturers and the retailers will want to sell different amounts to the demand markets from the amounts that the consumers at the demand markets want to purchase. However, these prices will adjust until the supply chain reaches equilibrium and the flows from the different mathematical programmes agree. |
| |
One way to find this equilibrium point is to solve a variational inequality . Theorem 1 gives the necessary variational inequalities:
Theorem 1: Variational Inequality The equilibrium state governing the supply chain model according to the optimality conditions of the supply chain mathematical programmes (?? REFLATEX{eq:manufacturer} not defined in eqn list ??), (?? REFLATEX{eq:retailer} not defined in eqn list ??) and (?? REFLATEX{eq:consumer} not defined in eqn list ??) is equivalent to the solution of the variational inequality problem given by: determine the equilibrium vectors of product shipments, shadow prices, and demand market prices . Theorem 1 gives the necessary variational inequalities:
Theorem 1: Variational Inequality The equilibrium state governing the supply chain model according to the optimality conditions of the supply chain mathematical programmes (?? REFLATEX{eq:manufacturer} not defined in eqn list ??), (?? REFLATEX{eq:retailer} not defined in eqn list ??) and (?? REFLATEX{eq:consumer} not defined in eqn list ??) is equivalent to the solution of the variational inequality problem given by: determine the equilibrium vectors of product shipments, shadow prices, and demand market prices 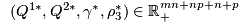 satisfying satisfying |
|
<
< | %BEGINLATEX%
\begin{equation*}
\begin{split}
& \sum_{i=1}^m \sum_{j=1}^n \left[ \frac{\partial f_i(Q^{1*})}{\partial q_{ij}} + \frac{\partial c_{ij}(q_{ij}^*)}{\partial q_{ij}} + \frac{\partial c_j(Q^{1*})}{\partial q_{ij}} - \gamma_j^* \right] \times \left[ q_{ij} - q_{ij}^* \right] \&+ \sum_{j=1}^n \sum_{k=1}^p \left[ c_{jk}(Q^{2*}) + \gamma_j^* - \rho_{3k}^* \right] \times \left[ q_{jk} - q_{jk}^* \right] \&+ \sum_{j=1}^n \left[ \sum_{i=1}^m q_{ij}^* - \sum_{k=1}^p q_{jk}^* \right] \times \left[ \gamma_j - \gamma_j^* \right] \&+ \sum_{k=1}^p \left[ \sum_{j=1}^n q_{jk}^* - d_k(\rho_3^*) \right] \times \left[ \rho_{3k} - \rho_{3k}^* \right] \geq 0, \forall (Q^{1}, Q^{2}, \gamma, \rho_{3}) \in \mathbb{R}_+^{mn+np+n+p}
\end{split}
\end{equation*} |
>
> | %BEGINLATEX% \begin{equation*} \begin{split} & \sum_{i=1}^m \sum_{j=1}^n \left[ \frac{\partial f_i(Q^{1*})}{\partial q_{ij}} + \frac{\partial c_{ij}(q_{ij}^*)}{\partial q_{ij}} + \frac{\partial c_j(Q^{1*})}{\partial q_{ij}} - \gamma_j^* \right] \times \left[ q_{ij} - q_{ij}^* \right] \ &+ \sum_{j=1}^n \sum_{k=1}^p \left[ c_{jk}(Q^{2*}) + \gamma_j^* - \rho_{3k}^* \right] \times \left[ q_{jk} - q_{jk}^* \right] \ &+ \sum_{j=1}^n \left[ \sum_{i=1}^m q_{ij}^* - \sum_{k=1}^p q_{jk}^* \right] \times \left[ \gamma_j - \gamma_j^* \right] \ &+ \sum_{k=1}^p \left[ \sum_{j=1}^n q_{jk}^* - d_k(\rho_3^*) \right] \times \left[ \rho_{3k} - \rho_{3k}^* \right] \geq 0, \forall (Q^{1}, Q^{2}, \gamma, \rho_{3}) \in \mathbb{R}_+^{mn+np+n+p} \end{split} \end{equation*} |
| | %ENDLATEX%
Once the equilibrium state has been found the manufacturers' prices and the retailers' prices can be calculated: |
| |
| META FILEATTACHMENT |
attachment="latexc4fcd1f7e80fa349b24cfaaf68ec5d28.png" attr="h" comment="" date="1207048331" name="latexc4fcd1f7e80fa349b24cfaaf68ec5d28.png" stream="GLOB(0x8e875a0)" tmpFilename="latexc4fcd1f7e80fa349b24cfaaf68ec5d28.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex109b7ce4252e22e2189597f1798107c1.png" attr="h" comment="" date="1207049196" name="latex109b7ce4252e22e2189597f1798107c1.png" stream="GLOB(0xa89a574)" tmpFilename="latex109b7ce4252e22e2189597f1798107c1.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex813a7e6cd57411a1b867f121059a868c.png" attr="h" comment="" date="1207049196" name="latex813a7e6cd57411a1b867f121059a868c.png" stream="GLOB(0xa89a580)" tmpFilename="latex813a7e6cd57411a1b867f121059a868c.png" user="MichaelOSullivan" version="1" |
|
|
<
< |
| META FILEATTACHMENT |
attachment="latexb5912e945e9329efa3deca443764042e.png" attr="h" comment="" date="1207049824" name="latexb5912e945e9329efa3deca443764042e.png" stream="GLOB(0xaaba7ac)" tmpFilename="latexb5912e945e9329efa3deca443764042e.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex26d615107ca4c212aad3419fc2885034.png" attr="h" comment="" date="1207049824" name="latex26d615107ca4c212aad3419fc2885034.png" stream="GLOB(0xaaba818)" tmpFilename="latex26d615107ca4c212aad3419fc2885034.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex533779377b97fd3c43de6837161d5078.png" attr="h" comment="" date="1207049824" name="latex533779377b97fd3c43de6837161d5078.png" stream="GLOB(0xaaba758)" tmpFilename="latex533779377b97fd3c43de6837161d5078.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latexa9c92bcfdc81177b4d2b139f7fa8b7f4.png" attr="h" comment="" date="1207050261" name="latexa9c92bcfdc81177b4d2b139f7fa8b7f4.png" stream="GLOB(0x9ad7050)" tmpFilename="latexa9c92bcfdc81177b4d2b139f7fa8b7f4.png" user="MichaelOSullivan" version="1" |
|
| |
| META FILEATTACHMENT |
attachment="latexdbde51c32699928974582b4a0d99f300.png" attr="h" comment="" date="1207050541" name="latexdbde51c32699928974582b4a0d99f300.png" stream="GLOB(0xa739abc)" tmpFilename="latexdbde51c32699928974582b4a0d99f300.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex59f03a8f6b43496526f96f273a850e5b.png" attr="h" comment="" date="1207050542" name="latex59f03a8f6b43496526f96f273a850e5b.png" stream="GLOB(0xa739b28)" tmpFilename="latex59f03a8f6b43496526f96f273a850e5b.png" user="MichaelOSullivan" version="1" |
| META FILEATTACHMENT |
attachment="latex1e01a2903b6d8b4f47b4e06511bb3e5f.png" attr="h" comment="" date="1207050542" name="latex1e01a2903b6d8b4f47b4e06511bb3e5f.png" stream="GLOB(0xa739a68)" tmpFilename="latex1e01a2903b6d8b4f47b4e06511bb3e5f.png" user="MichaelOSullivan" version="1" |
|



![\[ Q^1 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1n} \\ q_{21} & q_{22} & \cdots & q_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ q_{m1} & q_{m2} & \cdots & q_{mn} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexb682066036205339cf7d9bdcf6f1c0c2.png)
![\[ Q^1 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1n} \\ q_{21} & q_{22} & \cdots & q_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ q_{m1} & q_{m2} & \cdots & q_{mn} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexb682066036205339cf7d9bdcf6f1c0c2.png)
![\[ Q^2 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1p} \\ q_{21} & q_{22} & \cdots & q_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ q_{n1} & q_{n2} & \cdots & q_{np} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexd4ad75dc59dcc4e9ddbb8a8c79db2777.png)
![\[ Q^2 = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1p} \\ q_{21} & q_{22} & \cdots & q_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ q_{n1} & q_{n2} & \cdots & q_{np} \end{pmatrix} \]](/pub/OpsRes/SupplyChainMP/latexd4ad75dc59dcc4e9ddbb8a8c79db2777.png)