Sets in AMPL
- Description
- Declaring a Set
- Set Expressions
- Defining a Set
- Ordered Sets
- Set Example
- Restricted Sets
- Multi-Dimensional Sets
- Efficient Generation of Sets
Description
Sets are one of the most fundamental concepts in AMPL. They are used to index variables, constraints, parameters and sometimes other sets. Most expressions involve an operation being performed over a set. Sets allow for large mathematical programmes to be expressed concisely. Return to topDeclaring a Set
Sets are declared using theset keyword followed by a label, possibly some attributes and either a set literal or set expression. The most common attribute is set by the within keyword. This specifies that the set will only contain elements from the following set definition: set ARCS within NODES cross NODES; # Elements of ARCS must have both elements in NODESIf you need a multi-dimensional set, but don't have the 1-dimensional sets to construct it yet you can use the
dimen keyword: set ROUTES dimen 2;There are some other set attributes, but we will not use them. Set literals can be defined as a list of elements:
{'HOST', 'DEVICE', 'SWITCH', 'HUB', 'LINK', 'SUPERLINK'} or a sequence of numbers: param start; param end > start; param step; set NUMBERS := start .. end by step;If the
by step is missing, the step is assumed to be 1 set NUMBERS := 1..5; # NUMBERS = {1, 2, 3, 4, 5} Note Automatic set generation can only be done in the [[AMPLProcess#model][model environment] should this be a link? - Lauren , in the data environment you must define the set explicitly: set NUMBERS := 1 2 3 4 5; # NUMBERS = {1, 2, 3, 4 5}
Return to top
Set Expressions
Set expressions take the following form (which can be extended to higher dimensional sets):- Define the elements that make up the set, e.g.,
s in SUPPLY_NODES, before the colon:operator; - Use a logical expression (after the
:) to indicate if an element (or pair of elements, or “tuple” of elements) should be included in the set.
{ in , [ in , in , ...] : } Set expressions may also involve one or more _set operators_: - =A union B= gives the set of elements in either =A= or =B=;
- =A inter B= gives the set of elements in both =A= and =B=;
- =A diff B= gives the set of elements in =A= that are not in =B=;
- =A symdiff B= gives the set of elements in either =A= or =B= but not both;
- =A cross B= gives the two-dimensional set of all pairs =a=
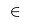 =A=, =b=
=A=, =b= 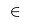 =B=. This can also be defined by ={a in A, b in B}=.
=B=. This can also be defined by ={a in A, b in B}=.
You will see examples of set expressions throughout the rest of this page.
[[#top][Return to top]]
------++ Defining a Set
Sets are usually defined in a data file:
set NODES := Youngstown Pittsburgh Cincinnati ‘Kansas City’ Chicago Albany Houston Tempe Gary ;
although they may be defined during declaration using either an explicit set literal or using a set expression: set KIND := {'HOST', 'DEVICE', 'SWITCH', 'HUB', 'LINK', 'SUPERLINK'}; set COMPONENT := {C in CLASSES : (kind[C] = 'HOST' ) or (kind[C] = 'DEVICE') or (kind[C] = 'HUB' ) or (kind[C] = 'SWITCH')}; set FABRIC := NODE union LINK; and sets may also be defined dynamically: set SEARCH within VERTICES; let SEARCH := {v in VERTICES: (v, w) in EDGES};
------+++ Defining 2-Dimensional Sets
There are three different ways to define 2-dimensional sets. The "best" way to use depends on the set. - *Using a List* You simply list the elements in the set. This is good for sparse sets.
model; set ARCS within NODES cros NODES; data; set ARCS := (Youngstown, Albany), (Youngstown, Cincinnati), ... ;
- *Using a Table* You give a table using the first index set for the rows and the second index set for the columns, then you place a =+= where an element exists and a =-= where there is no element. This is good for dense sets.
set ARCS: Cincinnati ‘Kansas City’ Chicago Albany Houston Tempe Gary := Youngstown + + + + - - - Pittsburgh + + + - - - + Cincinnati - - - + + - - ‘Kansas City’ - - - - + + - Chicago - - - - - + + ;
- *Using an Array* You define a list of column indices for each row index. This is a good for sets with a few elements for each row.
set ARCS := (Youngstown, *) Cincinnati ‘Kansas City’ Chicago Albany (Pittsburgh, *) Cincinnati ‘Kansas City’ Chicago Gary (Cincinnati, *) Albany Houston ...
[[#top][Return to top]]
------++ Ordered Sets
You can create sets where the elements are ordered using the =ordered= keyword during definition.
set MONTHS ordered;
AMPL will puts the elements in this set in the order they appear in the data file (or {\tt let} statement). AMPL also understands the following operations for ordered sets: ord(e, ORD_SET) # The position of e in ORD_SET first(ORD_SET) # The first element in ORD_SET last(ORD_SET) # The last element in ORD_SET prev(e, ORD_SET) # The element before e in ORD_SET next(e, ORD_SET) # The element after e in ORD_SET member(i, ORDSET) # The element at position i in ORD_SET
[[#top][Return to top]]
------++ Set Example
Consider the following AMPL statement from the [[AmericanSteelPlanningProblem][The American Steel Planning Problem]]. We use =ord= in the creation of =TIME_ARCS=:
# The set of time-staged arcs set TIME_ARCS within TIME_NODES cross TIME_NODES := { (m, t) in TIME_NODES, (n, u) in TIME_NODES : ( ( (m, n) in ARCS) and (t = u) ) or # The arcs used for transportation ( (m = n) and (ord(t, MONTHS) + 1 = ord(u, MONTHS)) )}; # The arcs used for storage There are many concepts within this one statement, let's look at them one at a time.
------+++ Set Operations
There are many operations we can perform on sets (see [[#expressions][Set Expressions]]). We have seen that =cross= creates all pairs of two sets, so =TIME_NODES cross TIME_NODES= creates a set of all pairs of =TIME_NODES=. Some set operations may be [[LoopingInAMPL][looped]] over indexing sets. For example, to generate all the transportation arcs in the time-staged network you could use the following statement
set TRANSPORT_ARCS := union {t in MONTHS} (union {(m, n) ARCS} {(m, t, n, t)}); or you could loop over {\tt MONTHS} and {\tt ARCS} simultaneously set TRANSPORT_ARCS := union {t in MONTHS, (m, n) in ARCS} {(m, t, n, t)};
------+++ Set Membership and Subsets
We have seen how loop over a set using the =in= keyword. This keyword also provides a [[LogicInAMPL][logical]] check if an element is in a set, e.g., =(m, n) in ARCS= is true if the pair =(m, n)= is in the set =ARCS= and false otherwise. We may restrict a set to be a subset of an existing set by using the keyword {\tt within}, e. g., set ARCS within NODES cross NODES;
means each arc is created between two nodes.
------+++ Ordered Set Operators
The final condition on =TIME_ARCS= ( (m = n) and (ord(t, MONTHS) + 1 = ord(u, MONTHS)) )};
creates the "storage" arcs. We could use next(t, MONTHS) = u or t = prev(u, MONTHS) except for a problem when =t= is =June= or =u= is =April=, respectively. When you use =prev= or =next= you must be careful of the first and last members of the set respectively. However, you can use =first= or =last= to check if you are using these elements. [[#top][Return to top]]
------++ Restricted Sets
When [[PrintingInAMPL][using display or printf statements]] we saw that we could restrict the members of a set being printed, e.g., display {(m, n) in ARCS : Supply[m] > 0}; # Display all arcs from supply nodes We can do this when creating sets, e. g., =TIME_NODES=, or when using a set as an index for variables, parameters or constraints. For example, rather than setting the upper bound of =UnderProduction= to be 0 for all non-supply nodes (since non-supply nodes don't produce anything) we could only create this variable for the supply nodes (in fact this may be preferable since there will be less variables). var UnderProduction {(n, t) in TIME_NODES : Supply[n, t] > 0} >= 0, integer; We could make sure this variable is only added to the constraints for the supply nodes (e.g., =ConserveFlow= constraints) by using a conditional expression. subject to ConserveFlow {(n, t) in TIME_NODES}: sum {(m, s) in TIME_NODES: (m, s, n, t) in TIME_ARCS} Shipment[m, s, n, t] + Supply[n, t] - if Supply[n, t] > 0 then UnderProduction[n, t] = ... [[#top][Return to top]]
------++ Multi-dimensional Sets
We have already seen different ways of [[#define][declaring 2-dimensional sets]]. We have now encountered higher dimensional sets, e.g., =TIME_ARCS= has 4 dimensions. We generated =TIME_ARCS= automatically, but we could have specified it using a data file. set TIME_ARCS within TIME_NODES cross TIME_NODES;
*List* set TIME_ARCS := (Youngstown, April, Albany, April) (Youngstown, April, Youngstown, May) ... ;
*Table* set TIME_ARCS : = (*, May, *, May) Cincinnati 'Kansas City' Albany ... := Youngstown + + + ... Pittsburgh + + - ... ... ;
*Array* set TIME_ARCS := (*, May, *, May) (Youngstown, Cincinnati) ... ... ;
or set TIME_ARCS := (Youngstown, May, *, May) Cincinnati ‘Kansas City’ ... ... ;
[[#top][Return to top]]
------++ Efficient Generation of Sets
When creating models, generating sets by looping over all possibilities and removing those that don't fit some conditions (e.g., like the =TIME_ARCS= statement) can take a long time if there are many possibilities. This is time that could be spent solving the model! If possible you should try to create sets by building them up from smaller building block, rather than by creating an enormous set and pruning it. For example, instead of using this statement # The set of time-staged arcs set TIME_ARCS within TIME_NODES cross TIME_NODES := { (m, t) in TIME_NODES, (n, u) in TIME_NODES : ( ( (m, n) in ARCS) and (t = u) ) or # The arcs used for transportation ( (m = n) and (ord(t, MONTHS) + 1 = ord(u, MONTHS)) )}; # The arcs used for storage to create =TIME_ARCS= you could use these statement set TRANSPORT_ARCS := union {t in MONTHS, (m, n) in ARCS} {(m, t, n, t)}; set STORAGE_ARCS := union {t in MONTHS, (m, n) in ARCS : t <> last(MONTHS)} {(m, t, n, next(t, MONTHS)}; set TIME_ARCS within TIME_NODES cross TIME_NODES := TRANSPORT_ARCS union STORAGE_ARCS; Rather than looping over all possibilities and only keeping those that are appropriate, the new statement only loops over smaller sets that can be used to build up the =TIME_NODES= set efficiently. [[#top][Return to top]]
-- Main.MichaelOSullivan - 27 Feb 2008
Ideas, requests, problems regarding TWiki? Send feedback

