
Difference: SurfboardProduction (26 vs. 27)
Revision 272010-07-25 - MichaelOSullivan
| Line: 1 to 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | |||||||||||
| Line: 89 to 89 | |||||||||||
| |*FORM FIELD ProblemDescription*|ProblemDescription|A surfboard manufacturer is planning his monthly surfboard production of Malibu and Super Thruster boards. He has limitations on his supply of fibreglass resin, having only 72 kilos left in stock. To construct a Malibu board requires 4 kilos of resin, and to build a Super Thruster one needs 3 kilos.
He has consulted a market research firm about the effect of the price he charges on the demand for the surfboards. They have provided him with the following information. If the price of a Malibu board is
The manufacturer has two decisions to make:
2. Formulate the Objective Function
The manufacturer wants to maximise his return from selling the surfboards. He does not want to have any left over as that is a waste of resin, so he will not make enough boards to satisfy demand. Thus, he assumes he will sell all the boards he makes. His return will be the number of boards of each type he makes multiplied by the price he chooses for that type of board:
3. Formulate the Constraints
The manufacturer only has 72 kilograms of resin to make his boards. Define a set of raw materials
The complete formulation is:
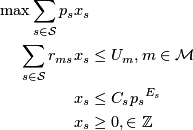 set SURFBOARDS; set MATERIALS;Next, we add the parameters for surfboards surfboard.mod:
param Coefficient {SURFBOARDS};
param Exponent {SURFBOARDS};
As well as the parameters for raw materials:
param Supply {MATERIALS};
and for the surfboard "recipe"
param Recipe {MATERIALS, SURFBOARDS};
Our final step, before implementing our formulation in surfboard.mod is to define the decision variables:
var Price {SURFBOARDS};
var Production {SURFBOARDS} >= 0, integer;
Now the formulation is straightforward:
maximize TotalProfit:
sum {s in SURFBOARDS} Price[s] * Production[s];
subject to MaterialSupply {m in MATERIALS} :
sum {s in SURFBOARDS} Recipe[m, s] * Production[s] <= Supply[m];
subject to SurfboardDemand {s in SURFBOARDS} :
Production[s] <= Coefficient[s] * (Price[s] ^ Exponent[s]);
Note Both the objective and the SurfboardDemand are nonlinear expressions.
The formulation data is specified in surfboard.dat. The sets are straightforward (note the use of ' to define the whitespace in Super Thruster):
set SURFBOARDS := Malibu 'Super Thruster' ; set MATERIALS := Resin ;and by defining multiple parameters at once we can define the demand equation parameters at the same time: param: Coefficient Exponent := Malibu 12000 -1.5 'Super Thruster' 12000 -1.8 ;Using a list to define the Supply parameter and a table to define the Recipe parameter completes surfboard.dat:
param Supply :=
Resin 72 ;
param Recipe :
Malibu 'Super Thruster' :=
Resin 3 4 ;
Since our mathematical programme is a nonlinear programme we cannot use CPLEX to solve our problem. In (the Student Edition) of AMPL we can use MINOS for nonlinear programming. The script file for solving this problem would typically be similar to:
reset; model surfboard.mod; data surfboard.dat; option solver minos; solve; display Price, Production;However, if you run this script file you will observe the following error: 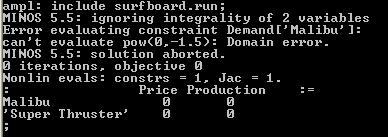 This error occurs because the initial values for
This error occurs because the initial values for Price (and Production) are set to 0. Both demand estimation functions have negative exponents, so are undefined for a value of 0, i.e.,
Price variables to be non-zero:
let Price['Malibu'] := 1; let Price['Super Thruster'] := 1;and resolve:  Note that MINOS does not actually solve for integer variables:
Note that MINOS does not actually solve for integer variables:
MINOS 5.5: ignoring integrality of 2 variablesbut both the Production variables both have integer values.
MINOS also terminated before determining optimality
MINOS 5.5: too many major iterations.By default, the number of major iterations allowed by MINOS is 50. If you increase the number of major iterations by changing the MINOS options: option minos_options 'major_iterations=100';and resolve you will notice that the price of the Super Thruster board is slowly increasing, as is the total return. By increasing the limit on the major iterations to 1500 we get the optimal solution: 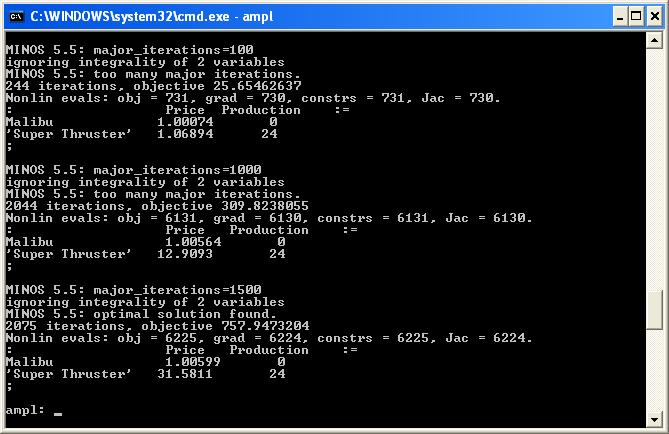 |
| | |||||||||||
| Changed: | |||||||||||
| < < | |*FORM FIELD Results*|Results|Our computational model shows that the optimal solution is to produce 24 Super Thruster boards and sell them for $31.5811 each. Note that this solution yields integer production values, but the optimal prices ($31.958 for the Super Thruster boards and $1.01 for the Malibu boards) seem low. We may have encountered a local optimum.
If the manufacturer only makes Malibu boards he has enough resin to make 18 boards. To get demand for 18 boards his price
  This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS server
This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS serversurfboard.mod and surfboard.dat as the model and data files and revise our script file
let Price['Malibu'] := 101.27; let Price['Super Thruster'] := 56.96; solve; display Price, Production;to solve using MINLP (on the NEOS Server) and find an optimal integer solution. You are using the solver minlp. Executing AMPL. processing data. processing commands. 4 variables, all nonlinear 3 constraints; 6 nonzeros 2 nonlinear constraints 1 linear constraint 1 nonlinear objective; 4 nonzeros. MINLP-B&B (20020703): m(before SOS) = 3 m(a f t e r SOS) = 3 Optimal solution found 3 subproblems, objective = 1665.141545 Evals: obj = 107, constr = 107, grad = 46, Hes = 45 : Price Production := Malibu 100 12 'Super Thruster' 58.1427 8 ;The manufacturer will most likely want a price that is to the nearest cent. It is dangerous to round mathematical programme solutions as even a small change in the variable value may result in a large change in the objective function or may even cause the solution to become infeasible. Since the Price variables cause our mathematical programme to be nonlinear, we will fix these variables and use CPLEX to solve for the Production variables:
reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.15; fix Price; solve; display Price, Production;Note that we rounded both up and down to check the "local neighbourhood" of the optimal point (see some discussion about solution accuracy). 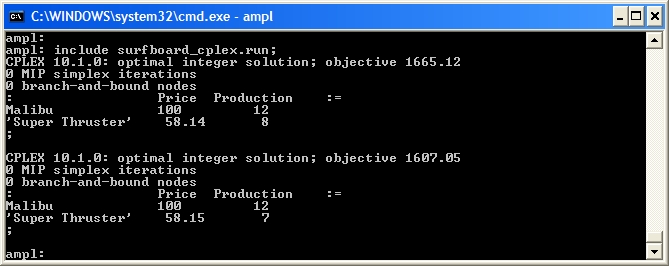 |
|Latex rendering error!! dvi file was not created. | ||||||||||
| > > | |*FORM FIELD Results*|Results|Our computational model shows that the optimal solution is to produce 24 Super Thruster boards and sell them for $31.5811 each. Note that this solution yields integer production values, but the optimal prices ($31.958 for the Super Thruster boards and $1.01 for the Malibu boards) seem low. We may have encountered a local optimum.
If the manufacturer only makes Malibu boards he has enough resin to make 18 boards. To get demand for 18 boards his price
 This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS server
This gives us a different optimal solution with a much higher return $1665.27. However, this solution does not give us integer production. Unfortunately, MINOS does not solve for integer variables. However, MINLP on the NEOS serversurfboard.mod and surfboard.dat as the model and data files and revise our script file
let Price['Malibu'] := 101.27; let Price['Super Thruster'] := 56.96; solve; display Price, Production;to solve using MINLP (on the NEOS Server) and find an optimal integer solution. You are using the solver minlp. Executing AMPL. processing data. processing commands. 4 variables, all nonlinear 3 constraints; 6 nonzeros 2 nonlinear constraints 1 linear constraint 1 nonlinear objective; 4 nonzeros. MINLP-B&B (20020703): m(before SOS) = 3 m(a f t e r SOS) = 3 Optimal solution found 3 subproblems, objective = 1665.141545 Evals: obj = 107, constr = 107, grad = 46, Hes = 45 : Price Production := Malibu 100 12 'Super Thruster' 58.1427 8 ;The manufacturer will most likely want a price that is to the nearest cent. It is dangerous to round mathematical programme solutions as even a small change in the variable value may result in a large change in the objective function or may even cause the solution to become infeasible. Since the Price variables cause our mathematical programme to be nonlinear, we will fix these variables and use CPLEX to solve for the Production variables:
reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.15; fix Price; solve; display Price, Production;Note that we rounded both up and down to check the "local neighbourhood" of the optimal point (see some discussion about solution accuracy).  |
| | ||||||||||
|*FORM FIELD Conclusions*|Conclusions|The Surfboard Production problem is a relatively simple problem to formulate, but its solution requires careful thought and analysis. The management summary surfboard.doc contains some information about the initial values used (so future consultants/researchers can follow the work) and details about the NEOS Optimization Server
param Objective {1..150, 1..150};
fix Price;
for {p in 1..150 by 1, q in 1..150 by 1} {
let Price['Malibu'] := p;
let Price['Super Thruster'] := q;
option solver cplex;
solve;
let Objective[p, q] := TotalProfit;
}
Using this picture we can try to discern if the optimal solution we found using MINLP (shown below) is the global optimum.
: Price Production := Malibu 100 12 'Super Thruster' 58.1427 8Hint This for loop may take a long time to finish. Also, you may want to print the TotalProfit parameter to a file using AMPL.
|
|*FORM FIELD StudentTasks*|StudentTasks|
| |||||||||||
| Line: 124 to 124 | |||||||||||
| |||||||||||
| Deleted: | |||||||||||
| < < |
| ||||||||||
| |||||||||||
| Added: | |||||||||||
| > > |
| ||||||||||
| |||||||||||
View topic | History: r29 < r28 < r27 < r26 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback