Difference: IntegerProgrammingWithAMPL (1 vs. 2)
Revision 22008-04-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming with AMPL | ||||||||
| Line: 16 to 16 | ||||||||
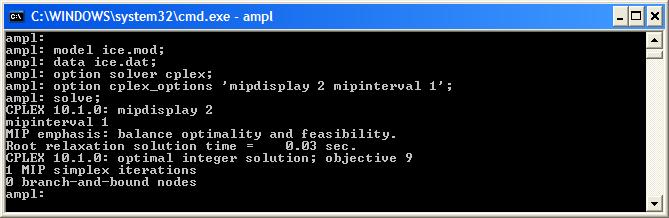
| Solving this problem with AMPL and CPLEX is very fast (it is only a small problem): | ||||||||
| Changed: | ||||||||
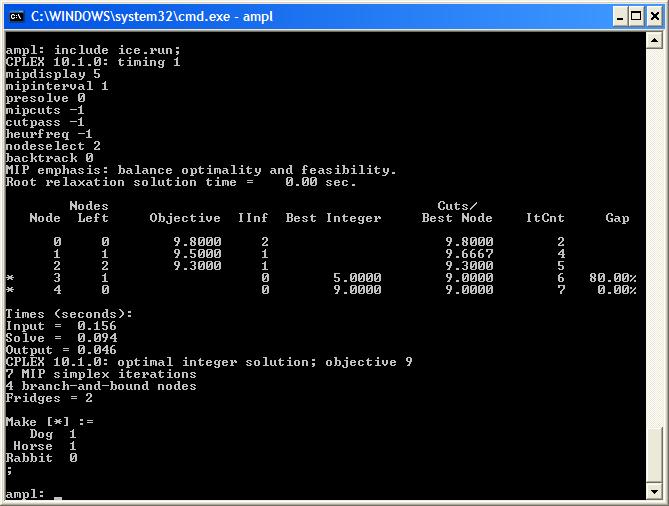
| < < |  However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch and bound tree. First, let’s remove all the CPLEX technology and re-solve our problem: ice.runWith all CPLEX’s “bells and whistles” removed we get a slightly larger branch-and-bound tree:
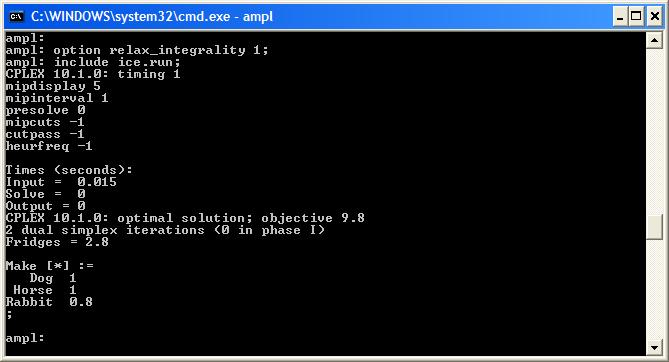
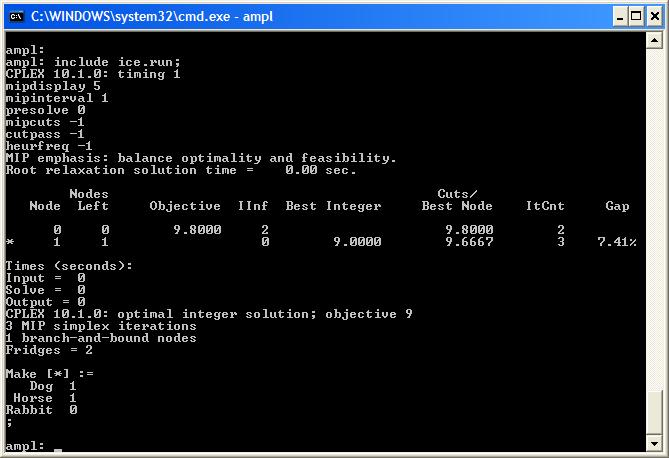
Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| |||||||
| > > |  | |||||||
| Changed: | ||||||||
| < < | -- MichaelOSullivan - 23 Apr 2008 | |||||||
| > > | However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch-and-bound tree. We will use this small example problem to demonstrate the effect of changing the default behaviour of CPLEX. | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | First, let's remove all the CPLEX technology and re-solve our problem using an AMPL script:
reset; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | solve; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | display Fridges, Make; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | With all CPLEXs "bells and whistles" removed we get a slightly larger branch-and-bound tree:
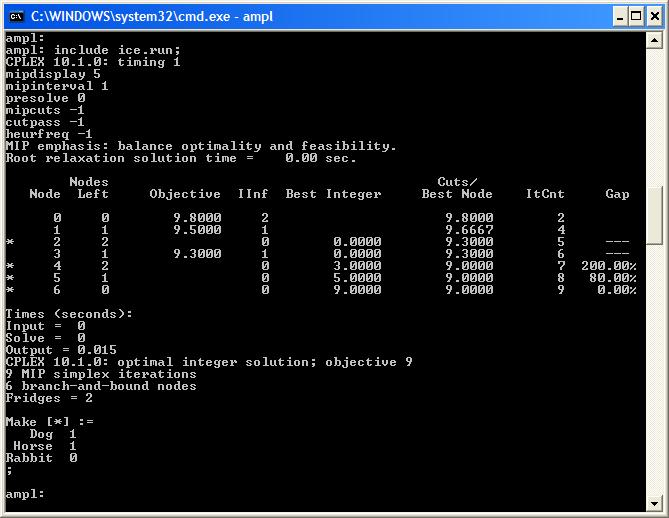 Let's look at ways to reduce the size of this branch-and-bound tree.
Let's look at ways to reduce the size of this branch-and-bound tree.Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| |||||||
| ||||||||
Revision 12008-04-23 - MichaelOSullivan
| Line: 1 to 1 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Added: | |||||||||||||||||
| > > |
Integer Programming with AMPLSpecifying variables to be integer or binary in AMPL will cause the solver, e.g., CPLEX, to use mixed-integer programming. This will often be enough to solve many of the problems you will encounter. However, if your integer programmes are taking a long time to solve you can use some "tricks" to speed up the branch-and-bound process.A "Simple" Integer ProgrammeTo demonstrate the techniques we can use to control integer programming we will look at a simple integer programming problem:Jim has three requests for frozen ice sculptures, his commission is $1000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit.The AMPL model and data files, ice.mod and ice.dat respectively, are attached. Solving this problem with AMPL and CPLEX is very fast (it is only a small problem):  However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch and bound tree. First, let’s remove all the CPLEX technology and re-solve our problem: ice.runWith all CPLEX’s “bells and whistles” removed we get a slightly larger branch-and-bound tree:
Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| ||||||||||||||||
Ideas, requests, problems regarding TWiki? Send feedback