
Difference: IntegerProgrammingWithAMPL (1 vs. 5)
Revision 52008-05-11 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming with AMPL | ||||||||
| Line: 8 to 8 | ||||||||
| To demonstrate the techniques we can use to control integer programming we will look at a simple integer programming problem: | ||||||||
| Changed: | ||||||||
| < < | Jim has three requests for frozen ice sculptures, his commission is $10000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit. | |||||||
| > > | Jim has three requests for frozen ice sculptures, his commission is $10000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit. | |||||||
| Changed: | ||||||||
| < < | The AMPL model and data files, ice.mod and ice.dat respectively, are attached. | |||||||
| > > | The AMPL model and data files, ice.mod and ice.dat respectively, are attached. | |||||||
| Solving this problem with AMPL and CPLEX is very fast (it is only a small problem): | ||||||||
| Changed: | ||||||||
| < < | 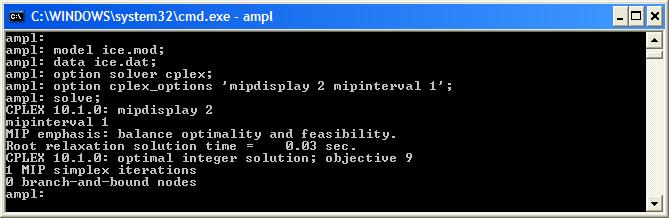 | |||||||
| > > |  | |||||||
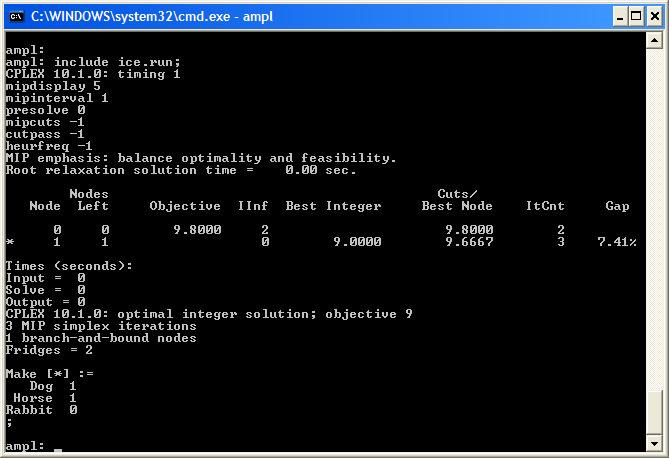
| However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch-and-bound tree. We will use this small example problem to demonstrate the effect of changing the default behaviour of CPLEX. First, let's remove all the CPLEX technology and re-solve our problem using an AMPL script: | ||||||||
| Changed: | ||||||||
| < < | reset; model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); solve; display Fridges, Make; | |||||||
| > > |
reset;
model ice.mod;
data ice.dat;
option solver cplex;
option presolve 0;
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1');
solve;
display Fridges, Make;
| |||||||
| With all CPLEXs "bells and whistles" removed we get a slightly larger branch-and-bound tree: | ||||||||
| Changed: | ||||||||
| < < | 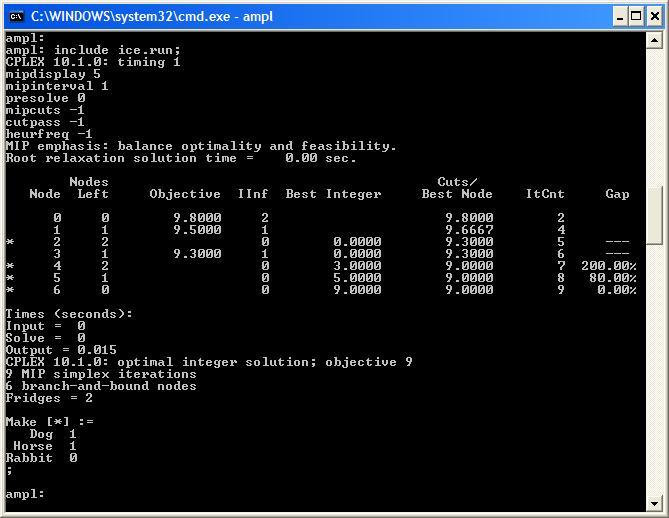 | |||||||
| > > |  | |||||||
| Let's look at ways to reduce the size of this branch-and-bound tree. | ||||||||
| Line: 33 to 51 | ||||||||
| If we look at the variables we can see where our solution is fractional: | ||||||||
| Changed: | ||||||||
| < < | 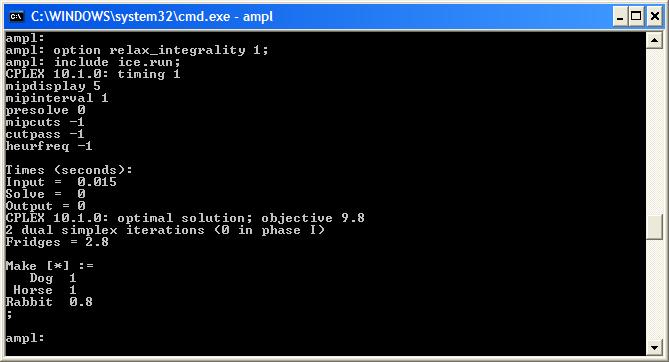 | |||||||
| > > |  | |||||||
| Changed: | ||||||||
| < < | As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the TotalWeight constraint (display TotalWeight.body;) we can see that the truck is at its weight limit. | |||||||
| > > | As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the TotalWeight constraint (display TotalWeight.body;) we can see that the truck is at its weight limit. | |||||||
It looks likely that we should only use 2 fridges. We can create some new suffixes to experiment with our hypothesis.
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let's add the priority suffix to our run file (before solving): | ||||||||
| Changed: | ||||||||
| < < | suffix priority IN, integer, >= 0, <= 9999;(now we can assign variables priorities ranging from 0 - least - to 9999 - most). Let's give the Fridges variable a priority of 100 and the Make variables a priority of 0: let Fridges.priority := 100; let {s in SCULPTURES} Make[s].priority := 0; | |||||||
| > > | suffix priority IN, integer, >= 0, <= 9999;(now we can assign variables priorities ranging from 0 - least - to 9999 - most). Let's give the Fridges variable a priority of 100 and the Make variables a priority of 0:
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
| |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
The branch-and-bound tree appears unchanged, so perhaps CPLEX had already branched on Fridges early in the branch-and-bound tree. However, we can try a breadth-first search of the tree, since this will try different values for Fridges before performing branching on other variables. Setting nodeselect to 2 (best estimate) and backtrack to 0 makes CPLEX perform a search very close to breadth-first (see The AMPL CPLEX User Guide | ||||||||
| Changed: | ||||||||
| < < | option cplex_options ('timing 1 mipdisplay 5 mipinterval 1 ' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1 ' & 'nodeselect 2 backtrack 0'); | |||||||
| > > |
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1 ' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1 ' &
'nodeselect 2 backtrack 0');
| |||||||
| Changed: | ||||||||
| < < | 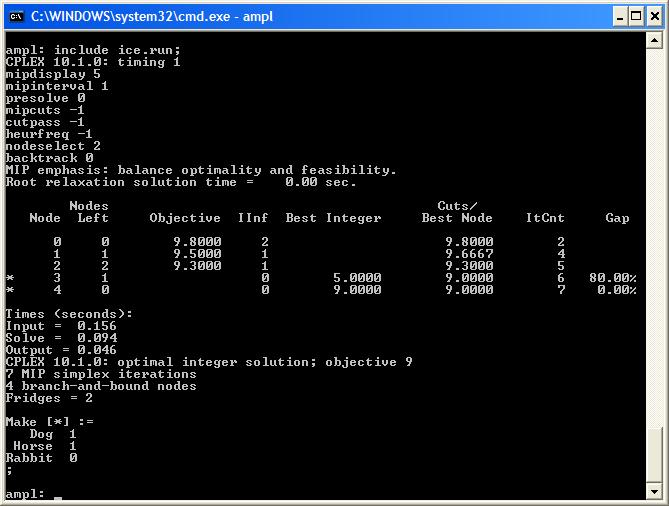 | |||||||
| > > |  | |||||||
| Now the tree has been fathomed earlier (it only has 4 nodes instead of 6). However, we are not sure if CPLEX branched down to 2 fridges first (our hypothetical optimum). To control the direction of the branches we can create a new suffix for the direction we should branch on each variable (-1 for down, 0 for no preference, 1 for up). | ||||||||
| Changed: | ||||||||
| < < | suffix direction IN, integer, >= -1, <= 1; | |||||||
| > > | suffix direction IN, integer, >= -1, <= 1; | |||||||
We can force a down branch first on Fridges: | ||||||||
| Changed: | ||||||||
| < < | let Fridges.direction := -1; | |||||||
| > > | let Fridges.direction := -1; | |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| This doesn't seem to have decreased the size of the branch-and-bound tree. Let's try one more thing. We have given CPLEX a good branch to try first, but we have not carefully considered what to do next. Let's remove the breadth-first search option and let CPLEX decide how to proceed: | ||||||||
| Changed: | ||||||||
| < < | reset; model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); suffix priority IN, integer, >= 0, <= 9999; suffix direction IN, integer, >= -1, <= 1; let Fridges.priority := 100; let {s in SCULPTURES} Make[s].priority := 0; let Fridges.direction := -1; solve; display Fridges, Make; | |||||||
| > > |
reset;
model ice.mod;
data ice.dat;
option solver cplex;
option presolve 0;
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1');
suffix priority IN, integer, >= 0, <= 9999;
suffix direction IN, integer, >= -1, <= 1;
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
let Fridges.direction := -1;
solve;
display Fridges, Make;
| |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Now we have reduced our branch-and-bound tree to a single node by making a good choice about our first variable branch and letting CPLEX proceed from there. | ||||||||
Revision 42008-05-11 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming with AMPL | ||||||||
| Line: 8 to 8 | ||||||||
| To demonstrate the techniques we can use to control integer programming we will look at a simple integer programming problem: | ||||||||
| Changed: | ||||||||
| < < | Jim has three requests for frozen ice sculptures, his commission is $1000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit. | |||||||
| > > | Jim has three requests for frozen ice sculptures, his commission is $10000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit. | |||||||
| Changed: | ||||||||
| < < | The AMPL model and data files, ice.mod and ice.dat respectively, are attached. | |||||||
| > > | The AMPL model and data files, ice.mod and ice.dat respectively, are attached. | |||||||
| Solving this problem with AMPL and CPLEX is very fast (it is only a small problem): | ||||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch-and-bound tree. We will use this small example problem to demonstrate the effect of changing the default behaviour of CPLEX. First, let's remove all the CPLEX technology and re-solve our problem using an AMPL script: | ||||||||
| Changed: | ||||||||
| < < |
reset;
model ice.mod;
data ice.dat;
option solver cplex;
option presolve 0;
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1');
solve;
display Fridges, Make;
| |||||||
| > > | reset; model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); solve; display Fridges, Make; | |||||||
| With all CPLEXs "bells and whistles" removed we get a slightly larger branch-and-bound tree: | ||||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Let's look at ways to reduce the size of this branch-and-bound tree. | ||||||||
| Line: 51 to 33 | ||||||||
| If we look at the variables we can see where our solution is fractional: | ||||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Changed: | ||||||||
| < < | As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the TotalWeight constraint (display TotalWeight.body;) we can see that the truck is at its weight limit. | |||||||
| > > | As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the TotalWeight constraint (display TotalWeight.body;) we can see that the truck is at its weight limit. | |||||||
It looks likely that we should only use 2 fridges. We can create some new suffixes to experiment with our hypothesis.
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let's add the priority suffix to our run file (before solving): | ||||||||
| Changed: | ||||||||
| < < | suffix priority IN, integer, >= 0, <= 9999;(now we can assign variables priorities ranging from 0 - least - to 9999 - most). Let's give the Fridges variable a priority of 100 and the Make variables a priority of 0:
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
| |||||||
| > > | suffix priority IN, integer, >= 0, <= 9999;(now we can assign variables priorities ranging from 0 - least - to 9999 - most). Let's give the Fridges variable a priority of 100 and the Make variables a priority of 0: let Fridges.priority := 100; let {s in SCULPTURES} Make[s].priority := 0; | |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
The branch-and-bound tree appears unchanged, so perhaps CPLEX had already branched on Fridges early in the branch-and-bound tree. However, we can try a breadth-first search of the tree, since this will try different values for Fridges before performing branching on other variables. Setting nodeselect to 2 (best estimate) and backtrack to 0 makes CPLEX perform a search very close to breadth-first (see The AMPL CPLEX User Guide | ||||||||
| Changed: | ||||||||
| < < |
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1 ' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1 ' &
'nodeselect 2 backtrack 0');
| |||||||
| > > | option cplex_options ('timing 1 mipdisplay 5 mipinterval 1 ' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1 ' & 'nodeselect 2 backtrack 0'); | |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Now the tree has been fathomed earlier (it only has 4 nodes instead of 6). However, we are not sure if CPLEX branched down to 2 fridges first (our hypothetical optimum). To control the direction of the branches we can create a new suffix for the direction we should branch on each variable (-1 for down, 0 for no preference, 1 for up). | ||||||||
| Changed: | ||||||||
| < < | suffix direction IN, integer, >= -1, <= 1; | |||||||
| > > | suffix direction IN, integer, >= -1, <= 1; | |||||||
We can force a down branch first on Fridges: | ||||||||
| Changed: | ||||||||
| < < | let Fridges.direction := -1; | |||||||
| > > | let Fridges.direction := -1; | |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| This doesn't seem to have decreased the size of the branch-and-bound tree. Let's try one more thing. We have given CPLEX a good branch to try first, but we have not carefully considered what to do next. Let's remove the breadth-first search option and let CPLEX decide how to proceed: | ||||||||
| Changed: | ||||||||
| < < |
reset;
model ice.mod;
data ice.dat;
option solver cplex;
option presolve 0;
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1');
suffix priority IN, integer, >= 0, <= 9999;
suffix direction IN, integer, >= -1, <= 1;
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
let Fridges.direction := -1;
solve;
display Fridges, Make;
| |||||||
| > > | reset; model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); suffix priority IN, integer, >= 0, <= 9999; suffix direction IN, integer, >= -1, <= 1; let Fridges.priority := 100; let {s in SCULPTURES} Make[s].priority := 0; let Fridges.direction := -1; solve; display Fridges, Make; | |||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Now we have reduced our branch-and-bound tree to a single node by making a good choice about our first variable branch and letting CPLEX proceed from there. | ||||||||
Revision 32008-04-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming with AMPL | ||||||||
| Line: 43 to 43 | ||||||||
 | ||||||||
| Changed: | ||||||||
| < < | Let's look at ways to reduce the size of this branch-and-bound tree.Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| |||||||
| > > | Let's look at ways to reduce the size of this branch-and-bound tree.
Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating usingoption relax_integrality 1;.
If we look at the variables we can see where our solution is fractional:
 As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the
As you can see we are using 2.8 fridge units for our 2.8 sculptures. Also, if we check the TotalWeight constraint (display TotalWeight.body;) we can see that the truck is at its weight limit.
It looks likely that we should only use 2 fridges. We can create some new suffixes to experiment with our hypothesis.
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let's add the priority suffix to our run file (before solving):suffix priority IN, integer, >= 0, <= 9999;(now we can assign variables priorities ranging from 0 - least - to 9999 - most). Let's give the Fridges variable a priority of 100 and the Make variables a priority of 0:
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
 The branch-and-bound tree appears unchanged, so perhaps CPLEX had already branched on
The branch-and-bound tree appears unchanged, so perhaps CPLEX had already branched on Fridges early in the branch-and-bound tree. However, we can try a breadth-first search of the tree, since this will try different values for Fridges before performing branching on other variables. Setting nodeselect to 2 (best estimate) and backtrack to 0 makes CPLEX perform a search very close to breadth-first (see The AMPL CPLEX User Guide
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1 ' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1 ' &
'nodeselect 2 backtrack 0');
 Now the tree has been fathomed earlier (it only has 4 nodes instead of 6). However, we are not sure if CPLEX branched down to 2 fridges first (our hypothetical optimum).
To control the direction of the branches we can create a new suffix for the direction we should branch on each variable (-1 for down, 0 for no preference, 1 for up).
Now the tree has been fathomed earlier (it only has 4 nodes instead of 6). However, we are not sure if CPLEX branched down to 2 fridges first (our hypothetical optimum).
To control the direction of the branches we can create a new suffix for the direction we should branch on each variable (-1 for down, 0 for no preference, 1 for up).
suffix direction IN, integer, >= -1, <= 1;We can force a down branch first on Fridges:
let Fridges.direction := -1;  This doesn't seem to have decreased the size of the branch-and-bound tree.
Let's try one more thing. We have given CPLEX a good branch to try first, but we have not carefully considered what to do next. Let's remove the breadth-first search option and let CPLEX decide how to proceed:
This doesn't seem to have decreased the size of the branch-and-bound tree.
Let's try one more thing. We have given CPLEX a good branch to try first, but we have not carefully considered what to do next. Let's remove the breadth-first search option and let CPLEX decide how to proceed:
reset;
model ice.mod;
data ice.dat;
option solver cplex;
option presolve 0;
option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' &
'presolve 0 mipcuts -1 cutpass -1 ' &
'heurfreq -1');
suffix priority IN, integer, >= 0, <= 9999;
suffix direction IN, integer, >= -1, <= 1;
let Fridges.priority := 100;
let {s in SCULPTURES} Make[s].priority := 0;
let Fridges.direction := -1;
solve;
display Fridges, Make;
 Now we have reduced our branch-and-bound tree to a single node by making a good choice about our first variable branch and letting CPLEX proceed from there.
As stated earlier, CPLEX does a lot of good things automatically for you. Often, these "tricks" will be enough to solve your mixed-integer programming problems. However, if your problem is taking a long time to solve, you can experiment with adding some of your own control to the branch-and-bound process. History has shown that problem-specific approaches often work very well for hard integer programmes.
Now we have reduced our branch-and-bound tree to a single node by making a good choice about our first variable branch and letting CPLEX proceed from there.
As stated earlier, CPLEX does a lot of good things automatically for you. Often, these "tricks" will be enough to solve your mixed-integer programming problems. However, if your problem is taking a long time to solve, you can experiment with adding some of your own control to the branch-and-bound process. History has shown that problem-specific approaches often work very well for hard integer programmes. | |||||||
| -- MichaelOSullivan - 23 Apr 2008 | ||||||||
Revision 22008-04-23 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Integer Programming with AMPL | ||||||||
| Line: 16 to 16 | ||||||||
| Solving this problem with AMPL and CPLEX is very fast (it is only a small problem): | ||||||||
| Changed: | ||||||||
| < < |  However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch and bound tree. First, let’s remove all the CPLEX technology and re-solve our problem: ice.runWith all CPLEX’s “bells and whistles” removed we get a slightly larger branch-and-bound tree:
Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| |||||||
| > > |  | |||||||
| Changed: | ||||||||
| < < | -- MichaelOSullivan - 23 Apr 2008 | |||||||
| > > | However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch-and-bound tree. We will use this small example problem to demonstrate the effect of changing the default behaviour of CPLEX. | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | First, let's remove all the CPLEX technology and re-solve our problem using an AMPL script:
reset; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | model ice.mod; data ice.dat; option solver cplex; option presolve 0; option cplex_options ('timing 1 mipdisplay 5 mipinterval 1' & 'presolve 0 mipcuts -1 cutpass -1 ' & 'heurfreq -1'); | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | solve; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | display Fridges, Make; | |||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > | With all CPLEXs "bells and whistles" removed we get a slightly larger branch-and-bound tree:
 Let's look at ways to reduce the size of this branch-and-bound tree.
Let's look at ways to reduce the size of this branch-and-bound tree.Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| |||||||
| ||||||||
Revision 12008-04-23 - MichaelOSullivan
| Line: 1 to 1 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Added: | |||||||||||||||||
| > > |
Integer Programming with AMPLSpecifying variables to be integer or binary in AMPL will cause the solver, e.g., CPLEX, to use mixed-integer programming. This will often be enough to solve many of the problems you will encounter. However, if your integer programmes are taking a long time to solve you can use some "tricks" to speed up the branch-and-bound process.A "Simple" Integer ProgrammeTo demonstrate the techniques we can use to control integer programming we will look at a simple integer programming problem:Jim has three requests for frozen ice sculptures, his commission is $1000, $7000 and $5000 respectively. He must hire a refrigeration unit to transport each one. The units cost $4000 each. The sculptures will be transported on a truck with capacity 1.7 tonnes and he estimates the total weight of each sculpture (including the refrigeration unit) to be 1 tonne, half a tonne and a quarter of a tonne respectively. Jim must decide which sculptures to make to maximize his profit.The AMPL model and data files, ice.mod and ice.dat respectively, are attached. Solving this problem with AMPL and CPLEX is very fast (it is only a small problem):  However, sometimes all the technology behind CPLEX does not work so well and we need to control the branch and bound tree. First, let’s remove all the CPLEX technology and re-solve our problem: ice.runWith all CPLEX’s “bells and whistles” removed we get a slightly larger branch-and-bound tree:
Looking at the LP RelaxationOften you can gain insight into the branch-and-bound process by considering the LP relaxation. You can relax integrality without reformulating using \begin{verbatim}
Priorities, Searching and DirectionsAMPL and CPLEX allow you to define a priority for your integer variables. This means that if more than one integer variable is fractional in a solution, CPLEX will branch on the highest priority variable first. Let’s add the priority {\tt suffix} to our run file (before solving): \begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
\begin{verbatim}
| ||||||||||||||||
Ideas, requests, problems regarding TWiki? Send feedback



