Difference: IntegerProgramming (15 vs. 16)

Revision 162008-03-20 - MichaelOSullivan

Line: 1 to 1
 
META TOPICPARENT name="MathematicalProgramming" 
<-- Ready to Review - done - Lauren-->

Integer Programming

Changed:
<
<		Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and currently a lot of research is focussing on finding "good"... - Lauren there is a lot of current research finding "good" ways to solve integer programmes.
>
>		Integer programmes are almost identical to linear programmes with one very important exception. Some of the decision variables in integer programmes can only have integer values. The variables are known as integer variables. Since most integer programmes contain a mix of real variables (i.e., that can have any real value) and integer variables they are often known as mixed integer programmes. While the change from a linear programming formulation is a minor one, the effect on the solution process is enormous. Integer programmes can be very difficult problems to solve and currently a lot of research is focussing on finding "good" ways to solve integer programmes.
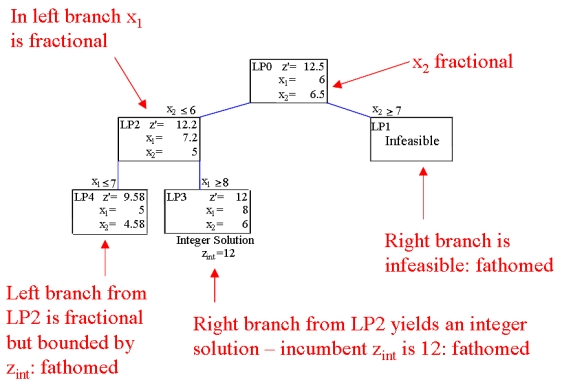
  Integer programming, the process of solving a (mixed) integer programme, was originally done using the branch-and-bound process. The branch part of the process eliminated non-integer values for integer variables in the following way:
  • Initially, all variables are left as real variables. The problem is solved using linear programming;
Line: 23 to 23
 The current best integer solution is called the incumbent. After solving a linear programme at a leaf node of the branch-and-bound tree one of the following conditions holds:
  • The linear programme is infeasible (no more branching is possible);
  • The linear programme solution is an integer solution with a better objective value than the incumbent. The incumbent is replaced with this new solution;
Changed:
<
<
  • The linear programme solution has a worse objective than the incumbent. Any nodes created from this node will also have a worse objective than the incumbent. This node is bounded by the incumbent objective;
>
>
  • The linear programme solution has an equal or worse objective than the incumbent. Any nodes created from this node will also have an equal or worse objective than the incumbent. This node is bounded by the incumbent objective;
 
  • The linear programme solution is fractional and has a better objective value than the incumbent. Further branching from this node is necessary to ensure an optimal solution is found.
Deleted:
<
<
  • A Tie? - Cam
  Only the last condition requires more branching, all the other conditions result in the node becoming fathomed and no more branching is required from that node.
Line: 34 to 33
 bandb.jpg

Integer Programming Topics

Changed:
<
<
>
>
 

Integer Programming with OR Software

Changed:
<
<
>
>
  To see integer programming in action, check out some of the integer programming case studies:
View topic | History: r23 < r22 < r21 < r20 | More topic actions...
 
This site is powered by the TWiki collaboration platform Powered by PerlCopyright © 2008-2025 by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding TWiki? Send feedback