Difference: IntegerProgramming (13 vs. 14)
Revision 142008-03-09 - LaurenJackson
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> | ||||||||
| Line: 16 to 16 | ||||||||
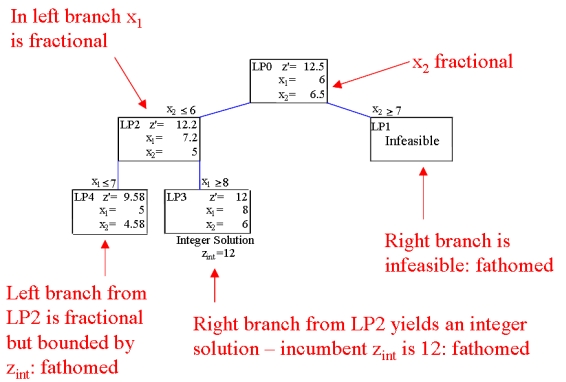
| Note For mixed integer programmes of any reasonable size this tree could be huge, in fact it grows exponentially as the number of integer variables increases. | ||||||||
| Changed: | ||||||||
| < < | The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimization principle: Adding constraints to a mathematical programming will result in a deterioration of the optimal objective value. | |||||||
| > > | The bounding process allows sections of the branch-and-bound tree to be removed from consideration before all the leaf nodes have integer solutions. It relies on the following optimisation principle: Adding constraints to a mathematical programme will result in a deterioration of the optimal objective value. | |||||||
| This means that adding the branching constraints to the linear programmes at the branch-and-bound tree nodes will mean the resulting nodes will have an optimal objective function value that is equal to or worse than the optimal objective function value of the original linear programme. Thus the objective function values get worse the deeper into the tree you look. Since we are finding the integer solution in the branch-and-bound tree with the best objective value, we can use any integer solutions to bound the tree. | ||||||||
| Line: 34 to 34 | ||||||||
Integer Programming Topics | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > |
| |||||||
Integer Programming with OR Software | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > |
| |||||||
| To see integer programming in action, check out some of the integer programming case studies: | ||||||||
View topic | History: r23 < r22 < r21 < r20 | More topic actions...
Copyright © 2008-2025 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding TWiki? Send feedback