| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Ready to Review --> |
| |
--> |
|
<
< | %BEGINLATEXPREAMBLE%
\usepackage{amsmath} |
>
> | %BEGINLATEXPREAMBLE% \usepackage{amsmath} |
| | %ENDLATEXPREAMBLE%
Case Study: The Coke Supply Chain Problem |
| |
|
|
<
< | |*FORM FIELD ExtraForExperts*|ExtraForExperts|This problem is similar to the Cosmic Computers Problem, but the facility location is a little different. Rather than face a decision about whether to build a plant or not, we need to determine what type of plant to build. This gives rise to the following variable:
While solving the Coke Supply Chain Problem, the expression
will often be fractional. This means that the capacity of the plant
where 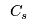 is the capacity of a plant of size is the capacity of a plant of size 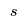 will be between the capacities of two different size plants, e.g., 280 kT/yr is between 225 kT/yr plant and a 300 kT/yr plant. We could use constraints to remove the fractionality, e.g.,
These branches will ensure plants have the right capacities, but will still not resolve fractionalities in the will be between the capacities of two different size plants, e.g., 280 kT/yr is between 225 kT/yr plant and a 300 kT/yr plant. We could use constraints to remove the fractionality, e.g.,
These branches will ensure plants have the right capacities, but will still not resolve fractionalities in the 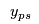 . However, if we want the capacity of plant . However, if we want the capacity of plant 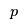 to be to be 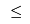 225, then we can remove all the 225, then we can remove all the 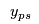 that allow for the capacity to be larger than 225:
Conversely, if we want to branch up, i.e., the capacity is that allow for the capacity to be larger than 225:
Conversely, if we want to branch up, i.e., the capacity is 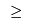 300, then we can remove all the 300, then we can remove all the 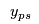 that allow the capacity to be smaller than 300:
Note For these branches to work properly, the possibility of building no plant must be modeled as building a plant with no capacity (i.e., that allow the capacity to be smaller than 300:
Note For these branches to work properly, the possibility of building no plant must be modeled as building a plant with no capacity (i.e., 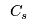 = 0) for no cost.
| = 0) for no cost.
| |
>
> | |*FORM FIELD ExtraForExperts*|ExtraForExperts|This problem is similar to the Cosmic Computers Problem, but the facility location is a little different. Rather than face a decision about whether to build a plant or not, we need to determine what type of plant to build. This gives rise to the following variable:
While solving the Coke Supply Chain Problem, the expression
will often be fractional. This means that the capacity of the plant
where 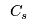 is the capacity of a plant of size is the capacity of a plant of size 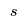 will be between the capacities of two different size plants, e.g., 280 kT/yr is between 225 kT/yr plant and a 300 kT/yr plant. We could use constraints to remove the fractionality, e.g.,
These branches will ensure plants have the right capacities, but will still not resolve fractionalities in the will be between the capacities of two different size plants, e.g., 280 kT/yr is between 225 kT/yr plant and a 300 kT/yr plant. We could use constraints to remove the fractionality, e.g.,
These branches will ensure plants have the right capacities, but will still not resolve fractionalities in the 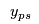 . However, if we want the capacity of plant . However, if we want the capacity of plant 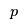 to be to be 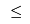 225, then we can remove all the 225, then we can remove all the 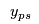 that allow for the capacity to be larger than 225:
Conversely, if we want to branch up, i.e., the capacity is that allow for the capacity to be larger than 225:
Conversely, if we want to branch up, i.e., the capacity is 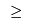 300, then we can remove all the 300, then we can remove all the 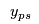 that allow the capacity to be smaller than 300:
Note For these branches to work properly, the possibility of building no plant must be modelled as building a plant with no capacity (i.e., that allow the capacity to be smaller than 300:
Note For these branches to work properly, the possibility of building no plant must be modelled as building a plant with no capacity (i.e., 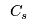 = 0) for no cost.
| = 0) for no cost.
| |
| | |*FORM FIELD StudentTasks*|StudentTasks|
- Write AMPL model, data and script files (
coke.mod, coke.dat and coke.run respectively) to solve the Coke Production Problem. Write a management summary for your solution.
What to hand in Your 3 AMPL files. Your management summary.
- Experts Only Solve the LP relaxation of the Coke Supply Chain Problem integer programme. Using the branches described in Extra for Experts, use AMPL to perform branching on at least 4 nodes and draw the resulting branch-and-bound tree.
Hint See Extra for Experts in the Cosmic ComputersProblem for an example of constraint branching in AMPL.
What to hand in Your AMPL code for implementing the branches. Your drawing of your branch-and-bound tree.
|
| META FILEATTACHMENT |
attachment="800px-Koks_Brennstoff.jpg" attr="h" comment="" date="1203500128" name="800px-Koks_Brennstoff.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\CokeProduction\800px-Koks_Brennstoff.jpg" size="77315" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\CokeProduction\800px-Koks_Brennstoff.jpg" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="coke_map.jpg" attr="h" comment="" date="1203500160" name="coke_map.jpg" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\CokeProduction\coke_map.jpg" size="43023" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\CokeProduction\coke_map.jpg" tmpFilename="" user="LaurenJackson" version="1" |
|

![\[ \begin{array}{r@{\,}l@{\quad\quad}l} \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\leq 225 & \text{(branching down)} \\ \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\geq 300 & \text{(branching up)} \end{array} \]](/pub/OpsRes/CokeSupplyChain/latexc6225364c4b2df199eec362b876b546b.png)
![\[ \begin{array}{r@{\,}l@{\quad\quad}l} \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\leq 225 & \text{(branching down)} \\ \displaystyle \sum_{s \in \text{sizes}} C_s y_{ps} &\geq 300 & \text{(branching up)} \end{array} \]](/pub/OpsRes/CokeSupplyChain/latexc6225364c4b2df199eec362b876b546b.png)