| |
|*FORM FIELD ProblemDescription*|ProblemDescription|*THE AMERICAN STEEL PROBLEM*
American Steel, an Ohio-based steel manufacturing company, produces steel at its two steel mills located at Youngstown and Pittsburgh. The company distributes finished steel to its retail customers through the distribution network of regional and field warehouses shown below:
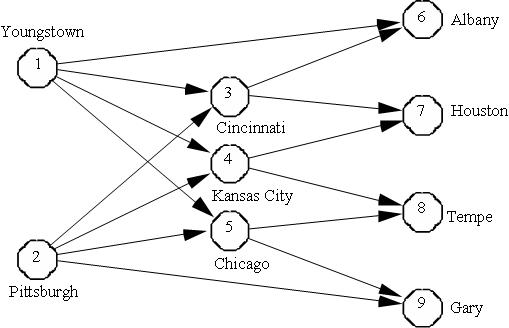 The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
| From node |
To node |
Cost |
Minimum |
Maximum |
| Youngstown |
Albany |
500 |
- |
1000 |
| Youngstown |
Cincinnati |
350 |
- |
3000 |
| Youngstown |
Kansas City |
450 |
1000 |
5000 |
| Youngstown |
Chicago |
375 |
- |
5000 |
| Pittsburgh |
Cincinnati |
350 |
- |
2000 |
| Pittsburgh |
Kansas City |
450 |
2000 |
3000 |
| Pittsburgh |
Chicago |
400 |
- |
4000 |
| Pittsburgh |
Gary |
450 |
- |
2000 |
| Cincinnati |
Albany |
350 |
1000 |
5000 |
| Cincinnati |
Houston |
550 |
- |
6000 |
| Kansas City |
Houston |
375 |
- |
4000 |
| Kansas City |
Tempe |
650 |
- |
4000 |
| Chicago |
Tempe |
600 |
- |
2000 |
| Chicago |
Gary |
120 |
- |
4000 |
The current monthly demand at American Steel’s four field warehouses is as follows:
| Field Warehouses |
Monthly Demand |
| Albany, N.Y. |
3000 |
| Houston |
7000 |
| Tempe |
4000 |
| Gary |
6000 |
The Youngstown and Pittsburgh mills can produce up to 10,000 tons and 15,000 tons of steel per month, respectively. The management wants to know the least cost monthly shipment plan.|
|*FORM FIELD ProblemFormulation*|ProblemFormulation|*1. IDENTIFY THE DECISION VARIABLES*
The decision variables for this problem are the same as for the transportation problem, the Flow of goods (cases of beer in The Beer Distribution Problem, tons of steels here) through the network. In ???LINK??? A Transportation Problem all arcs from the supply nodes to the demand nodes existed (although in ???LINK??? Forestry Management we used upper bounds to removes some arcs). In The American Steel Problem, the network has transshipment nodes and arcs don't exist between all nodes. However, arcs must travel from one node to another. In AMPL we ???LINK??? declare the set of NODES and the set of ARCS between nodes:
# The set of all nodes in the network
set NODES;
# The set of arcs in the network
set ARCS within NODES cross NODES;
Now we define bounds on the flow (of our goods) along each arc:
# The minimum and maximum flow allowed along the arcs
param Min {ARCS} integer, default 0;
param Max {(m, n) in ARCS} integer, >= Min[m, n], default Infinity;
and finally declare our Flow variables:
# The flow of goods to be sent across an arc
var Flow {(m, n) in ARCS} >= Min[m, n], <= Max[m, n], integer;
2. FORMULATE THE OBJECTIVE FUNCTION
The objective of transshipment problems in general and The American Steel Problem in particular is to minimise the cost of shipping goods through the network:
# The cost of shipping 1 unit of goods (per time unit)
param Cost {ARCS};
# Minimise the total shipping cost
minimize TotalCost:
sum {(m, n) in ARCS} Cost[m, n] * Flow[m, n];
3. FORMULATE THE CONSTRAINTS
All the nodes have supply and demand, demand = 0 for supply nodes, supply = 0 for demand nodes and supply = demand = 0 for transshipment nodes. Also, the supply and demand amounts must be integer to ensure a naturally integer solution (i.e., linear programming will provide an integer optimal solution).
# Each node has a (non-negative, integer) supply and a (non-negative, integer) demand
# Note. supply nodes have demand = 0 and vice versa,
# transshipment nodes have supply = demand = 0
param Supply {NODES} >= 0, integer, default 0;
param Demand {NODES} >= 0, integer, default 0;
The only constraints in the transshipment problem are flow conservation constraints. These constraints
simply state that the flow of goods into a node must be greater than the flow of goods out of a node.
# Must conserve flow in the network (goods cannot disappear!)
subject to ConserveFlow {n in NODES}:
sum {m in NODES: (m, n) in ARCS} Flow[m, n] + Supply[n] =>
sum {p in NODES: (n, p) in ARCS} Flow[n, p] + Demand[n];
For example, if a node has a supply of 10 units and has 10 units flowing in, then it can have no more than 20 units flowing out:
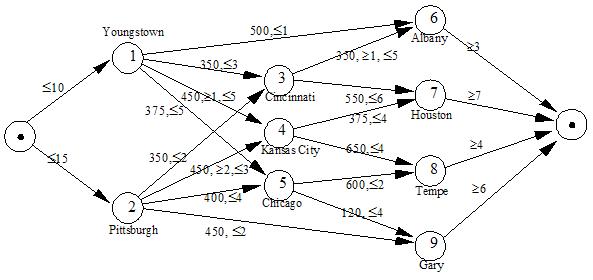
 Transshipment problems are often presented as a network formulation:
Transshipment problems are often presented as a network formulation:
 4. IDENTIFY THE DATA
The nodes of The American Steel Problem can be easily ???LINK??? defined using a list :
4. IDENTIFY THE DATA
The nodes of The American Steel Problem can be easily ???LINK??? defined using a list :
set NODES := Youngstown Pittsburgh
Cincinnati 'Kansas City' Chicago
Albany Houston Tempe Gary ;
Note that Kansas City must be enclosed in ' and ' because of the whitespace in the name.
The arc set is 2-dimensional and can be ???LINK??? defined in a number of different ways :
# List of arcs
set ARCS := (Youngstown, Albany), (Youngstown, Cincinnati), ... , (Chicago, Gary) ;
# Table of arcs
set ARCS: Cincinnati 'Kansas City' Chicago Albany Houston Tempe Gary :=
Youngstown + + + + - - -
Pittsburgh + + + - - - +
Cincinnati - - - + + - -
'Kansas City' - - - - + + -
Chicago - - - - - + + ;
# Array of arcs
set ARCS :=
(Youngstown, *) Cincinnati 'Kansas City' Chicago Albany
(Pittsburgh, *) Cincinnati 'Kansas City' Chicago Gary
.
.
.
(Chicago, *) Tempe Gary
;
We can choose lists, tables or arrays to define the parameters for The American Steel Problem,
but in this case we will use a list and ???LINK??? define multiple parameters
at once. This allows us to "cut-and-paste" the parameters from the problem description. Note the use of
. for parameters where the defaults will suffice (e.g., Min['Youngstown', 'Albany']):
param: Cost Min Max:=
Youngstown Albany 500 . 1000
Youngstown Cincinnati 350 . 3000
Youngstown 'Kansas City' 450 1000 5000
Youngstown Chicago 375 . 5000
Pittsburgh Cincinnati 350 . 2000
Pittsburgh 'Kansas City' 450 2000 3000
Pittsburgh Chicago 400 . 4000
Pittsburgh Gary 450 . 2000
Cincinnati Albany 350 1000 5000
Cincinnati Houston 550 . 6000
'Kansas City' Houston 375 . 4000
'Kansas City' Tempe 650 . 4000
Chicago Tempe 600 . 2000
Chicago Gary 120 . 4000
;
Note that the cost is in $/1000 ton, so we must divide the cost by 1000 before solving:
let {(m, n) in ARCS} Cost[m, n] := Cost[m, n] / 1000;
| |

 The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
 Transshipment problems are often presented as a network formulation:
Transshipment problems are often presented as a network formulation:
 4. IDENTIFY THE DATA
The nodes of The American Steel Problem can be easily ???LINK??? defined using a list :
4. IDENTIFY THE DATA
The nodes of The American Steel Problem can be easily ???LINK??? defined using a list :