The Transportation Problem
Introduction
The transportation problem is one of the simplest forms of network optimisation. The network is bi-partite, i.e., it can be split into two sets of nodes with all arcs going from one set to the other. One set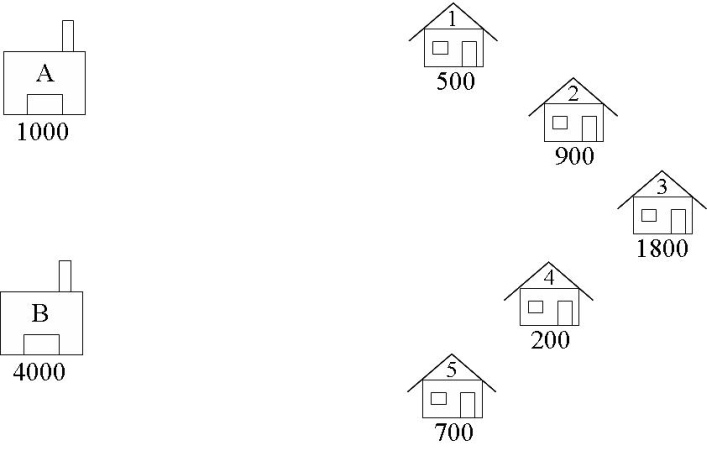 The arcs in the Brewery Problem carry crates of beer from the supply nodes (warehouses) to the demand nodes (bars) as shown in Figure 2. In this problem there are no restrictions of the arcs, so
The arcs in the Brewery Problem carry crates of beer from the supply nodes (warehouses) to the demand nodes (bars) as shown in Figure 2. In this problem there are no restrictions of the arcs, so 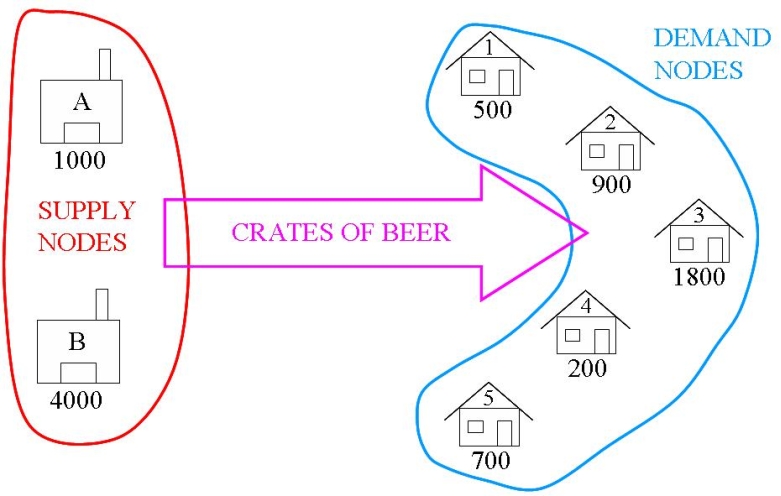 In the transportation problem there is a cost
In the transportation problem there is a cost Formulating the Transportation Problem
Transportation problem are network optimisation problems. Network optimisation problems are solved using mathematical programming. Thus, to formulate a transportation problem we use the 4 steps for formulating a mathematical programme:- Identify the Decision Variables
- Formulate the Objective Function
- Formulate the Constraints
- Identify the Data
Identify the Decision Variables
The decision variables in the transportation problem are the quantity of goods to carry along each arc, i.e.,Formulate the Objective Function
The objective in the transportation problem is to minimise the total transportation cost along the arcs, i.e.,Formulate the Constraints
The constraints in the transportation are simple: 1) use all the supply of goods; 2) meet all the demand of goods. These may be expressed concisely: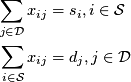
Identify the Data
The data for the transportation problem is also straightforward to determine. We need to identify the supply nodesUnbalanced Transportation Problems
The transportation problem we consider here must be balanced, i.e.,Restricting the Arcs
The arcs between the supply nodes and demand nodes may be restricted in two ways:- there may be bounds on the amount of goods that an arc may carry;
- some arcs may not exist, i.e., there is no way to transport goods from a particular supply node to a particular demand node.
Naturally Integer Solutions
The transportation problem is often an integer programme as the quantity of good delivered along the arcs must be integer. However, if the supply, demand and variable bounds are integer, then the transportation problem will have naturally integer solutions. This means that any solution found using linear programming will have integer values. This is a property that is common to other network optimisation problems, e.g., the transshipment problem.Solving the Transportation Problem with OR Software
To see examples of transportation problems, check out some of the transportation problem case studies:Results from OpsRes web retrieved at 02:56 (GMT)
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
\usepackage{amsmath} Case Study: Submitted: Operations Research Topics: Application Areas: Contents Problem Description Problem Description Return...
Number of topics: 2
-- MichaelOSullivan - 02 Apr 2008This topic: OpsRes > WebHome > NetworkOptimisation > TransportationProblem
Topic revision: r12 - 2008-04-22 - TWikiAdminUser
Ideas, requests, problems regarding TWiki? Send feedback