Case Study: Simple Health Clinic – Scheduled Appointments
Submitted: 10 Sep 2017
Application Areas: Healthcare
Contents
Problem Description
This case study extends the
Simple Health Clinic (SHC) model. In that case study walk-up patents waited for treatment by a doctor. In this case study an additional doctor is present in the clinic, one that sees patients with scheduled appointments. The second doctor can also treat walk up patients if they are free.
The goal of this simulation study is to analyse the average time patients spend:
- waiting for treatment; and
- in the clinic;
and the average length of the patient queue (which informs waiting room size). This analysis will include a comparison of the walk-up vs scheduled patients.
Return to top
Problem Formulation
In order to formulate a simulation model we specify the following components:
- Background – problem description
- Objectives of the study
- Expected benefits
- The CM: inputs, outputs, content, assumptions, simplifications’
- Experiments to run
Components 1(Background – problem description) and 2 (Objectives of the study) are given in the
Problem Description section (see paragraph describing the goal of the simulation study to identify study objectives).
The Expected benefits (component 3) are a virtual environment for evaluating patient waiting times, total time patients spend in the clinic, and the number of patients waiting for treatment. This environment can be used to experiment with changes to the clinic, including a comparison of effects on the waiting times, queue length, etc for the walk-up vs the scheduled patients.
The CM content is specified using the following components:
- Component List
- Process flow diagram
- Logic flow diagram
- Activity cycle diagram
Component List
The components of the Simple Health Clinic model are:
- Walk-up patients with their (inter)arrival times
- Scheduled patients with their appointment times
- Doctors with their treatment times
- Waiting room with its capacity
Process Flow Diagram
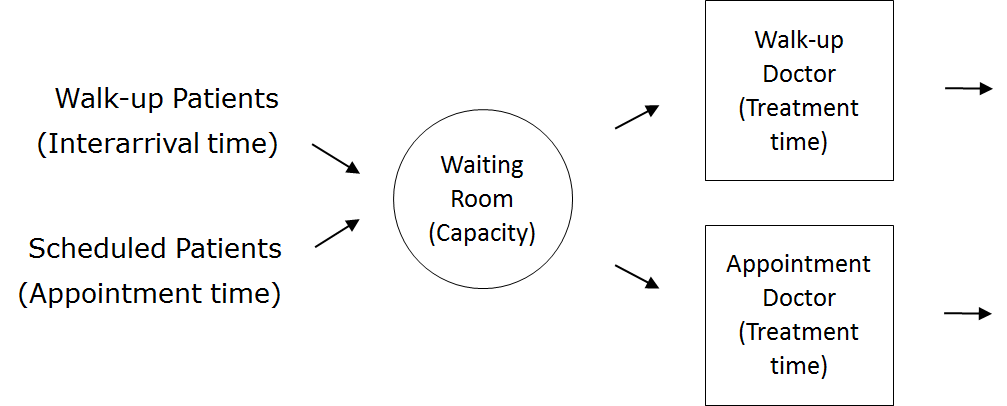
| Patient Logic Flow Diagram | | Doctor Logic Flow Diagrams |
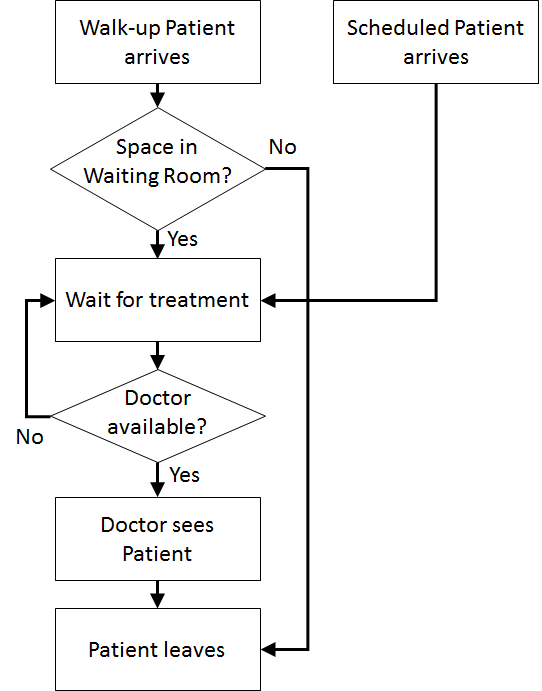 | | 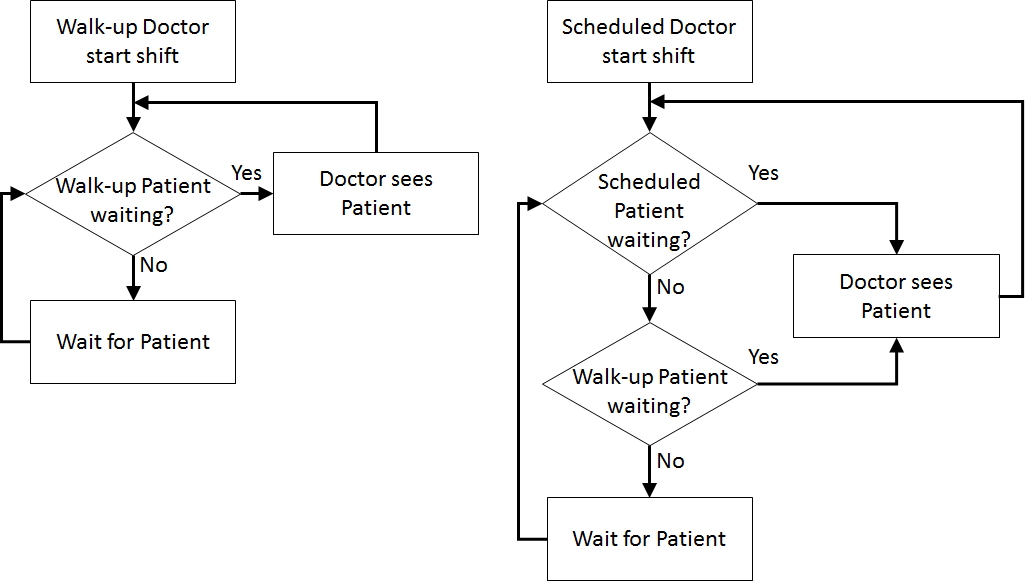 |
Activity Cycle Diagram

Once the content has been established (note this is usually an iterative process) we can identify the inputs and outputs: appointment times, interarrival times, treatment times, waiting times (Patient arrives to Doctor sees patient), total clinic time (Patient arrives to Outside), number in waiting room.
Assumptions are used to define stochasticity (e.g., Exponential interarrivals, Triangular treatment times) and the simplifications keep the system simple (e.g., one doctor on all day, no registration, no prioritisation).
Return to top
Computational Model
Start with the
Simple Health Clinic JaamSim model.
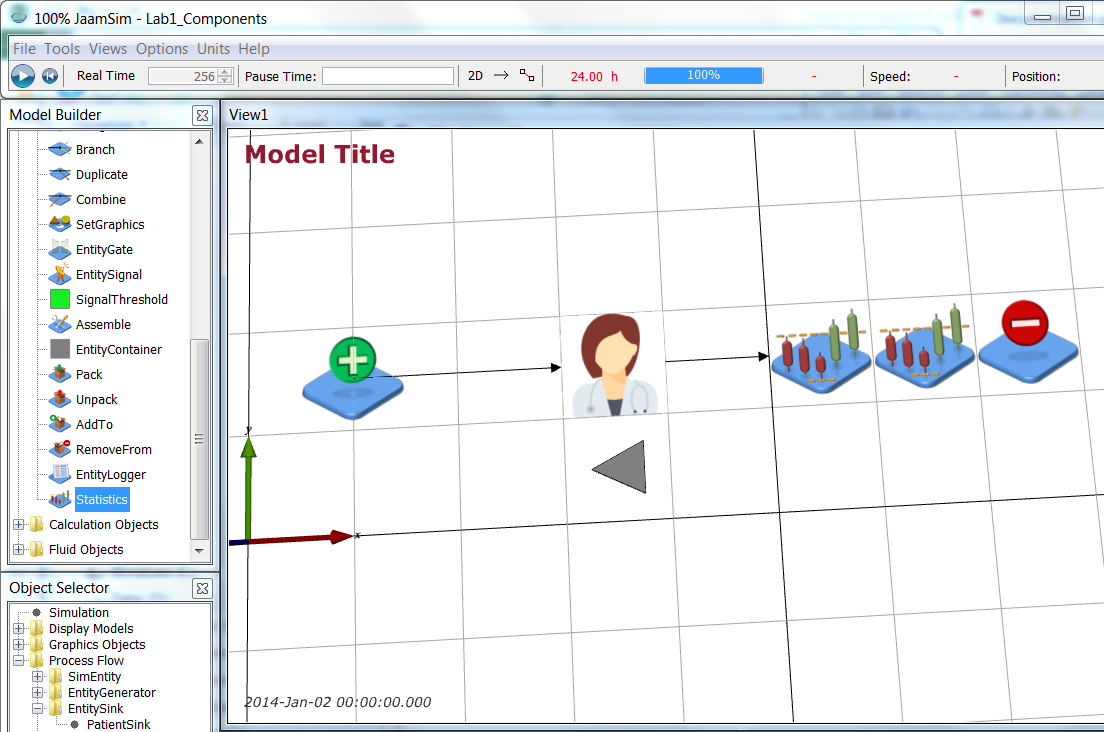
Rename the PatientGenerator object PatientWalkup. Now add a second EntityGenerator (ProcessFlow > EntityGenerator) and name it PatientAppointment. You can position it at 1 -0.5 0 m (Input Editor > Graphics > Position). Add an EventSchedule object (BasicObjects > EventSchedule) at 1 -1.5 0 m and name it AppointmentTimes.
Note To move objects within the View1 window with the mouse, hold down Ctrl and click on the object with the left mouse button. Keep the mouse button down when moving the object around.
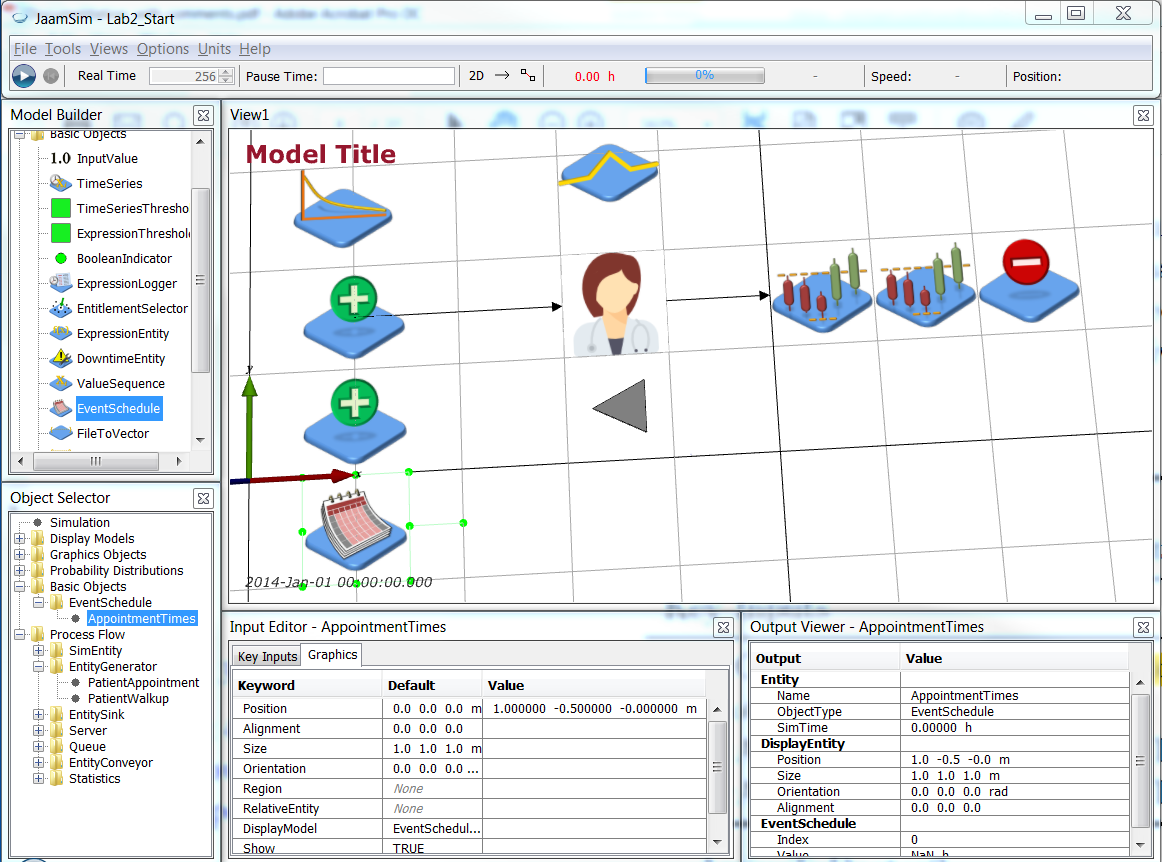
Save your simulation.
Now add a second doctor (Process Flow > Server) at 3.5 -0.5 0 m, name it Doctor2 and give it the
doctor2.png (icon made by Freepik from www.flaticon.com).
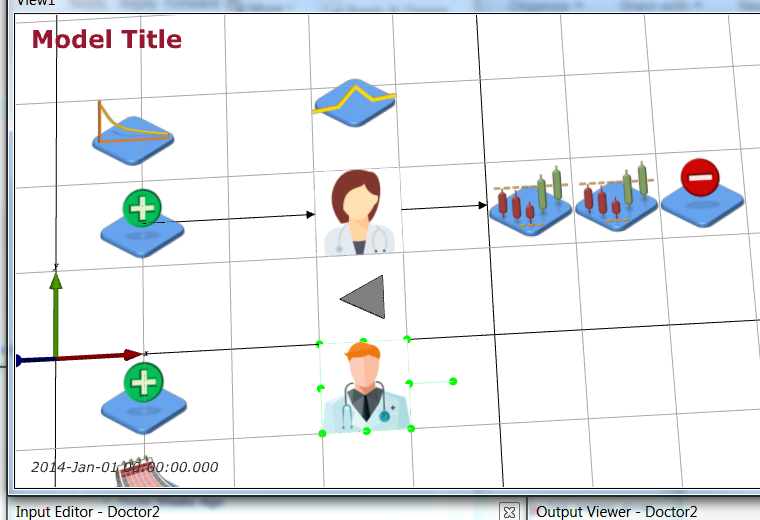
Save your simulation.
Next, add a new EntityConveyor (Process Flow > EntityConveyor) from PatientAppointment to Doctor2 as shown and update Key Inputs so that patients are generated at PatientAppointment and flow to Doctor2 across ArriveToTreat2. The EventSchedule object requires an input called TimeList which defines times in the simulation at which events occur. The EventSchedule object provides the inter-arrival times for the specified sequence of event times to the EntityGenerator object to create the entities at the specified times. In this case we want to use data from a separate file to define the appointment times so the TimeList input is left blank. Also, give Doctor2 the same treatment time as Doctor.
| Object |
Graphics |
Key Inputs |
| PatientAppointment |
|
NextComponent = ArriveToTreat2, PrototypeEntity = PatientEntity, FirstArrivalTime = AppointmentTimes, InterArrivalTime = AppointmentTimes |
| AppointmentTimes |
|
TimeList =, CycleTime = 24 h |
| ArriveToTreat2 |
Points = { 1 -0.5 0.000 m } { 3 -0.5 0.000 m }, DisplayModel = ArrowModelDefault |
NextComponent = Doctor2, StateAssignment = Arrive, TravelTime = 2 min |
| Doctor2 |
|
StateAssignment = Treat, ServiceTime = '([Simulation].RunIndex(1) == 1) || ([Simulation].RunIndex(1) == 2) ? 15[min] : [TreatmentDist].Value' |
Once the EventSchedule object is set up as described above save the simulation model. In the resulting .cfg file the following two lines should have been added (although they will not be lines 1 and 2).
1: Define EventSchedule { AppointmentTimes }
2: AppointmentTimes CycleTime { 24 h }
Open your .cfg file with Notepad++, find these lines and add the following line after them
3: Include '.\AppointmentTimes.inc'
This line tells the config file to look for a file called
AppointmentTime.inc and include all of the text in that file at this point in the config file. Download the
AppointmentTimes.inc file into the same directory as your .cfg file.
AppointmentTimes.inc defines the TimeList for the AppointmentTimes object. If an appointment time needs to be changed then we can change the corresponding time in the AppointmentTimes.inc file. Alternatively if we have a list of appointment times saved elsewhere, for example in an Excel file, then they can be copied and pasted into the .inc file. Note that the appointment times are repeated every 24 hours according to
AppointmentTimes.inc.
Save your .cfg file. You then need to reopen the file for the change to be added (otherwise the next time you save the Include statement will be lost from the .cfg file).
Now that scheduled patients are arriving according to their appointment times, we want to be able to distinguish between walk-up and scheduled patients. Add an (empty string) PatientType attribute to the PatientEntity object by setting Key Inputs > AttributeDefinitionList:
Next we add two Assign objects (Process Flow > Assign) named AssignWalkup and AssignAppointment respectively. We position these between the Patient generators and the ArriveToTreat* conveyors both graphically and in the NextComponent values.
| Object |
Graphics |
Key Inputs |
| PatientWalkup |
Position = 0 1.5 0.000000 m |
NextComponent = AssignWalkup |
| PatientAppointment |
Position = 0 -0.5 0.000000 m |
NextComponent = AssignAppointment |
| AssignWalkup |
Position = 1 1.5 0.000000 m |
NextComponent = ArriveToTreat, AttributeAssignmentList = { 'this.obj.PatientType = [[ Walkup ]]' } |
| AssignAppointment |
Position = 1 -0.5 0.000000 m |
NextComponent = ArriveToTreat2, AttributeAssignmentList = { 'this.obj.PatientType = [[ Appointment ]]' } |
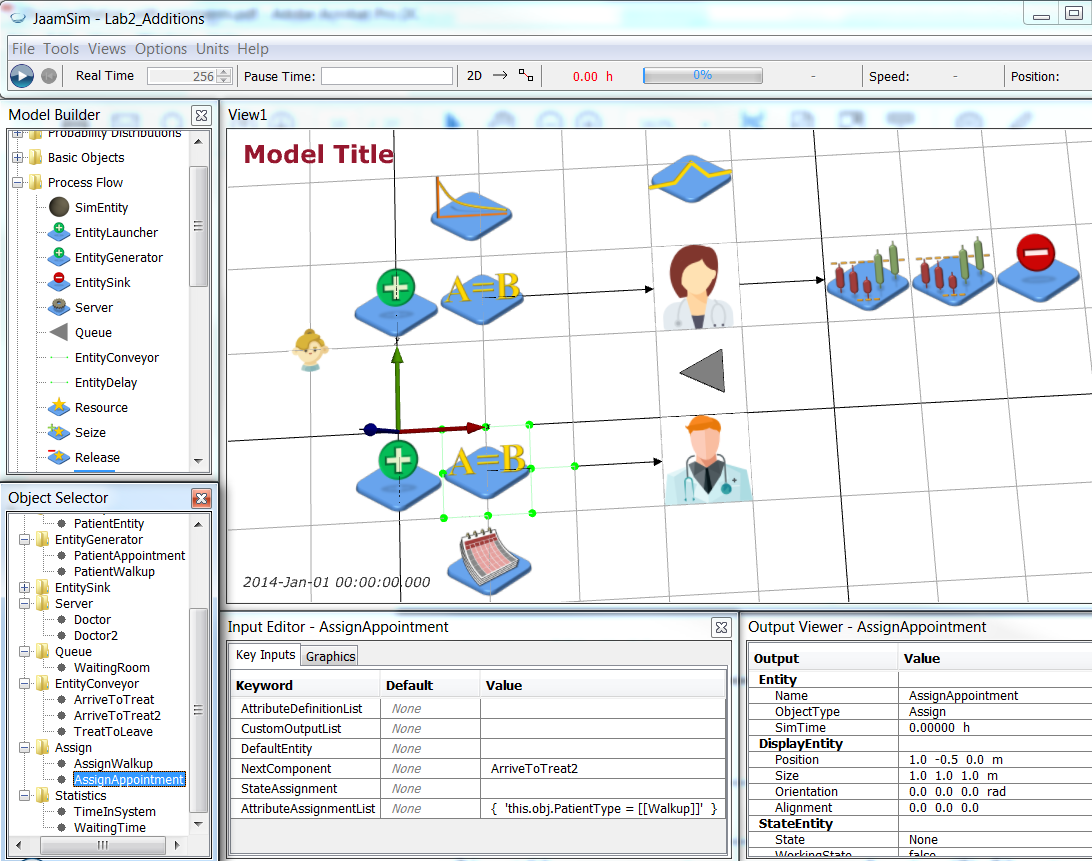
Save your simulation.
Now we will rename the WaitingRoom Queue object to be WalkupQueue and create a new Queue object AppointmentQueue at 3.5 -1.5 0 m. Make sure to set the StateAssignment of AppointmentQueue to Wait. Set the WaitQueue for Doctor2 to be AppointmentQueue.
Next we need to duplicate the statistic gathering for the walkup patients to get similar statistics for the scheduled patients. Select the TreatToLeave EntityConveyor, right click and select Duplicate. Rename the duplicate TreatToLeave2 and adjust the y-position of its Points to be -0.5. Repeat this for the two Statistics objects to create TimeInSystem2 and WaitingTime2 at 5.5 -0.5 0 m and 6.5 -0.5 0 m respectively. Finally, repeat this for the PatientSink object (at 7.5 -0.5 0 m), but rename the two EntitySink objects to be PatientWalkupSink (the old one) and PatientAppointmentSink (the duplicate) respectively.
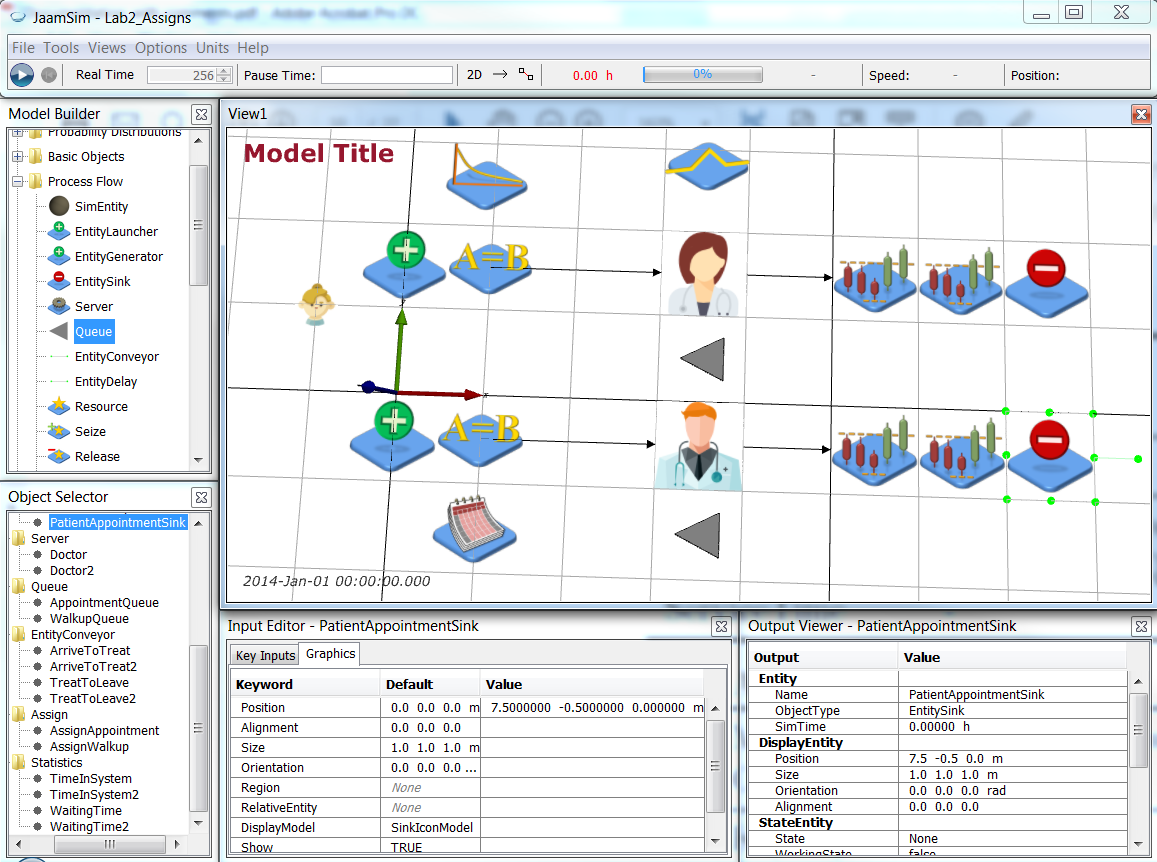
You will need to change the NextComponent Key Values of the duplicate objects as follows:
| Object |
Graphics |
Key Inputs |
| Doctor2 |
|
NextComponent = TreatToLeave2 |
| TreatToLeave2 |
Points = { 4 -0.5 0.000 m } { 5 -0.5 0.000 m } |
NextComponent = TimeInSystem2 |
| TimeInSystem2 |
Position = 5.5 -0.5 0.000 m |
NextComponent = WaitingTime2 |
| WaitingTime2 |
Position = 6.5 -0.5 0.000 m |
NextComponent = PatientAppointmentSink |
| PatientAppointmentSink |
Position = 7.5 -0.5 0.000 m |
|
Save your simulation.
Your simulation now models walkup and scheduled patients being seen by the two doctors separately. You can run your simulation and look at the data file. Recall you used 4 different scenarios in the Simple Health Clinic model and the 4th scenario used stochasticity for both (walkup) arrivals and treatment. Set the Simulation > Multiple Runs as follows:
This means you run 10 replications of scenario 4 (with “full” stochasticity). However, you also need to save the results from the new Statistics objects. Modify the Key Inputs of the Simulation object to get the schedule patients metrics:
| Object |
Key Inputs |
Value |
| Simulation |
GlobalSubstreamSeed |
[Simulation].RunIndex(2) |
| |
UnitTypeList |
DimensionlessUnit TimeUnit TimeUnit DimensionlessUnit DimensionlessUnit |
| |
|
TimeUnit TimeUnit DimensionlessUnit DimensionlessUnit |
| |
RunOutputList |
{ [Simulation].RunIndex(1) } |
| |
|
{ [!WaitingTime]. SampleAverage } |
| |
|
{ [!TimeInSystem].!SampleAverage } |
| |
|
{ [!WalkupQueue].!QueueLengthAverage } |
| |
|
{ [Doctor].Utilisation } |
| |
|
{ [!WaitingTime2].!SampleAverage } |
| |
|
{ [!TimeInSystem2].!SampleAverage } |
| |
|
{ [!AppointmentQueue].!QueueLengthAverage } |
| |
|
{ [Doctor2].Utilisation } |
Save your simulation.
Run your simulation and check the .dat file produced. Your file should look like this:
[Simulation].RunIndex(1) [WaitingTime].SampleAverage [TimeInSystem].SampleAverage [WalkupQueue].QueueLengthAverage [Doctor].Utilisation [WaitingTime2].SampleAverage [TimeInSystem2].SampleAverage [AppointmentQueue].QueueLengthAverage [Doctor2].Utilisation
h h h h
4.0 0.38405366237816774 0.6721529048440543 0.9121274481481481 0.6061936453819444 0.047831163832528174 0.3245097069847021 0.15544167377314747 0.708565400474537
4.0 0.8219966959851419 1.111039798239664 3.3573313594560186 0.914729190023148 0.05137962716586152 0.3368832764814815 0.16999437075231413 0.7295867157986111
4.0 0.18231854541459366 0.4643737348009948 0.5110314945717589 0.697349794861111 0.07290953726190474 0.3614429387301587 0.21870704035879557 0.7456867161226852
4.0 0.15044009060931898 0.4276216531630824 0.4109386495486115 0.6289475324884258 0.04596554312698413 0.3103043237142857 0.13695675836805501 0.6782827043171296
4.0 0.4608621209795323 0.7449073896929822 1.476147013425926 0.7928060206018518 0.039782093476307186 0.3159904990808823 0.15987477151620322 0.6977464573611111
4.0 0.24241772078282825 0.5456477393939393 0.5555406101273154 0.6252009754629629 0.043423220472222225 0.32121606757142857 0.133963723576388 0.7131016586921296
4.0 0.2614094597649572 0.5324488160085471 0.7079839535300925 0.6422825157523149 0.054203878703703696 0.34166384512479875 0.17248607967592514 0.740839141724537
4.0 0.49628468288742683 0.7857048559283626 1.8466593722685183 0.813790779212963 0.04087929695238095 0.320092180547619 0.11923128277777673 0.7245560956712963
4.0 0.20900518749619484 0.4944611306506849 0.6357241119675925 0.7685583299768518 0.07885540460547506 0.38238973465378434 0.25053211532407277 0.7798800384722222
4.0 0.535308072422222 0.8215745958333336 1.6954733292245368 0.8028416117592593 0.029352889542253516 0.29911107867370895 0.08683563156249953 0.6977800132175925
Now, you can observe and compare the performance of the clinic for both Walk-Up and Appointment patients using
Lab2Analysis.R. Make sure to edit the path and file name at the top of the
Lab2Analysis.R. Your output should have the following values:
and your paired t-test results should look as follows:
> t.test(Lab2scen$WalkUp.WaitingTime, Lab2scen$Appointment.WaitingTime, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.WaitingTime and Lab2scen$Appointment.WaitingTime
t = 4.7393, df = 9, p-value = 0.00106
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1693243 0.4785784
sample estimates:
mean of the differences
0.3239514
|
> t.test(Lab2scen$WalkUp.TimeInSystem, Lab2scen$Appointment.TimeInSystem, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.TimeInSystem and Lab2scen$Appointment.TimeInSystem
t = 4.713, df = 9, p-value = 0.0011
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1708939 0.4863719
sample estimates:
mean of the differences
0.3286329
|
> t.test(Lab2scen$WalkUp.Queue, Lab2scen$Appointment.Queue, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.Queue and Lab2scen$Appointment.Queue
t = 3.5743, df = 9, p-value = 0.005984
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3856432 1.7153436
sample estimates:
mean of the differences
1.050493
|
> t.test(Lab2scen$Doctor.Utilisation, Lab2scen$Doctor2.Utilisation, paired=TRUE)
Paired t-test
data: Lab2scen$Doctor.Utilisation and Lab2scen$Doctor2.Utilisation
t = 0.23657, df = 9, p-value = 0.8183
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.06565234 0.08098743
sample estimates:
mean of the differences
0.007667545
|
Finally, you need to enable the Appointment doctor to also see Walk-Up patients. Rename the Doctor2 Server as Doctor2Appointment and then Duplicate this Server to create Doctor2Walkup. Set Doctor2Walkup’s WaitQueue Value to WalkupQueue so it servers Walk-Up patients.
We control access to the Doctor2* Server objects using ExpressionThresholds. Add two ExpressionThresholds (with the Basic Object palette) and name them AppointmentThreshold and WalkupThreshold respectively. They are positioned at 2.5 -1.0 0.0 m and 2.5 -2.0 0.0 m respectively.
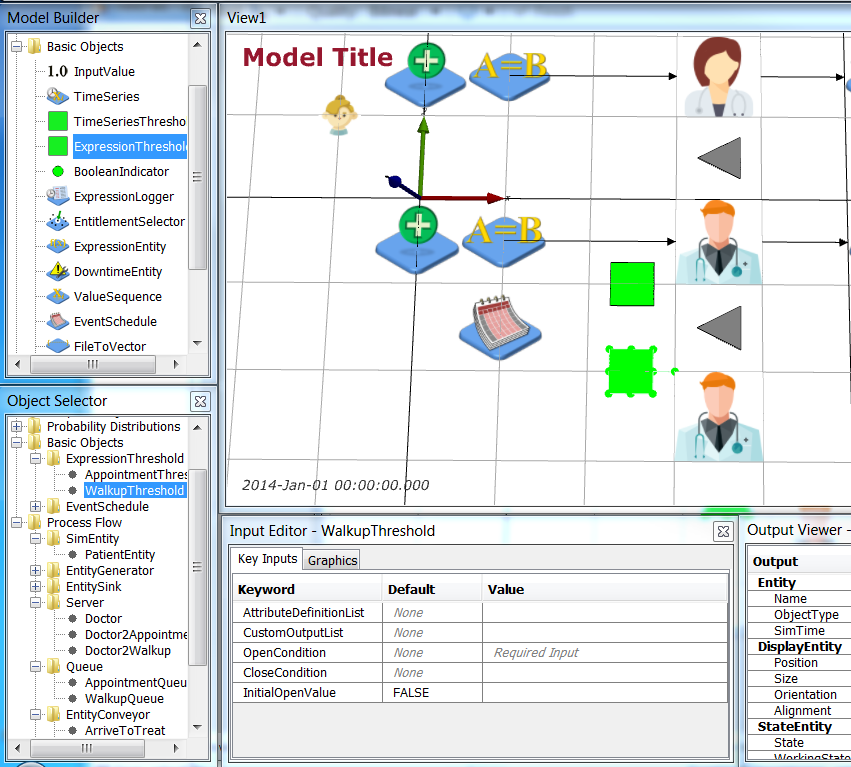 Return to top
Return to top
Results
[Simulation].RunIndex(1) [WaitingTime].SampleAverage [TimeInSystem].SampleAverage [WalkupQueue].QueueLengthAverage [Doctor].Utilisation [WaitingTime2].SampleAverage [TimeInSystem2].SampleAverage [AppointmentQueue].QueueLengthAverage [Doctor2].Utilisation
h h h h
4.0 0.38405366237816774 0.6721529048440543 0.9121274481481481 0.6061936453819444 0.047831163832528174 0.3245097069847021 0.15544167377314747 0.708565400474537
4.0 0.8219966959851419 1.111039798239664 3.3573313594560186 0.914729190023148 0.05137962716586152 0.3368832764814815 0.16999437075231413 0.7295867157986111
4.0 0.18231854541459366 0.4643737348009948 0.5110314945717589 0.697349794861111 0.07290953726190474 0.3614429387301587 0.21870704035879557 0.7456867161226852
4.0 0.15044009060931898 0.4276216531630824 0.4109386495486115 0.6289475324884258 0.04596554312698413 0.3103043237142857 0.13695675836805501 0.6782827043171296
4.0 0.4608621209795323 0.7449073896929822 1.476147013425926 0.7928060206018518 0.039782093476307186 0.3159904990808823 0.15987477151620322 0.6977464573611111
4.0 0.24241772078282825 0.5456477393939393 0.5555406101273154 0.6252009754629629 0.043423220472222225 0.32121606757142857 0.133963723576388 0.7131016586921296
4.0 0.2614094597649572 0.5324488160085471 0.7079839535300925 0.6422825157523149 0.054203878703703696 0.34166384512479875 0.17248607967592514 0.740839141724537
4.0 0.49628468288742683 0.7857048559283626 1.8466593722685183 0.813790779212963 0.04087929695238095 0.320092180547619 0.11923128277777673 0.7245560956712963
4.0 0.20900518749619484 0.4944611306506849 0.6357241119675925 0.7685583299768518 0.07885540460547506 0.38238973465378434 0.25053211532407277 0.7798800384722222
4.0 0.535308072422222 0.8215745958333336 1.6954733292245368 0.8028416117592593 0.029352889542253516 0.29911107867370895 0.08683563156249953 0.6977800132175925
Now, you can observe and compare the performance of the clinic for both Walk-Up and Appointment patients using
Lab2Analysis.R. Make sure to edit the path and file name at the top of the
Lab2Analysis.R. Your output should have the following values:
and your paired t-test results should look as follows:
> t.test(Lab2scen$WalkUp.WaitingTime, Lab2scen$Appointment.WaitingTime, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.WaitingTime and Lab2scen$Appointment.WaitingTime
t = 4.7393, df = 9, p-value = 0.00106
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1693243 0.4785784
sample estimates:
mean of the differences
0.3239514
|
> t.test(Lab2scen$WalkUp.TimeInSystem, Lab2scen$Appointment.TimeInSystem, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.TimeInSystem and Lab2scen$Appointment.TimeInSystem
t = 4.713, df = 9, p-value = 0.0011
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1708939 0.4863719
sample estimates:
mean of the differences
0.3286329
|
> t.test(Lab2scen$WalkUp.Queue, Lab2scen$Appointment.Queue, paired=TRUE)
Paired t-test
data: Lab2scen$WalkUp.Queue and Lab2scen$Appointment.Queue
t = 3.5743, df = 9, p-value = 0.005984
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3856432 1.7153436
sample estimates:
mean of the differences
1.050493
|
> t.test(Lab2scen$Doctor.Utilisation, Lab2scen$Doctor2.Utilisation, paired=TRUE)
Paired t-test
data: Lab2scen$Doctor.Utilisation and Lab2scen$Doctor2.Utilisation
t = 0.23657, df = 9, p-value = 0.8183
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.06565234 0.08098743
sample estimates:
mean of the differences
0.007667545
|
Return to top
Conclusions
In conclusion...
Return to top



 Once the content has been established (note this is usually an iterative process) we can identify the inputs and outputs: appointment times, interarrival times, treatment times, waiting times (Patient arrives to Doctor sees patient), total clinic time (Patient arrives to Outside), number in waiting room.
Assumptions are used to define stochasticity (e.g., Exponential interarrivals, Triangular treatment times) and the simplifications keep the system simple (e.g., one doctor on all day, no registration, no prioritisation).
Return to top
Once the content has been established (note this is usually an iterative process) we can identify the inputs and outputs: appointment times, interarrival times, treatment times, waiting times (Patient arrives to Doctor sees patient), total clinic time (Patient arrives to Outside), number in waiting room.
Assumptions are used to define stochasticity (e.g., Exponential interarrivals, Triangular treatment times) and the simplifications keep the system simple (e.g., one doctor on all day, no registration, no prioritisation).
Return to top
 Rename the PatientGenerator object PatientWalkup. Now add a second EntityGenerator (ProcessFlow > EntityGenerator) and name it PatientAppointment. You can position it at 1 -0.5 0 m (Input Editor > Graphics > Position). Add an EventSchedule object (BasicObjects > EventSchedule) at 1 -1.5 0 m and name it AppointmentTimes.
Note To move objects within the View1 window with the mouse, hold down Ctrl and click on the object with the left mouse button. Keep the mouse button down when moving the object around.
Rename the PatientGenerator object PatientWalkup. Now add a second EntityGenerator (ProcessFlow > EntityGenerator) and name it PatientAppointment. You can position it at 1 -0.5 0 m (Input Editor > Graphics > Position). Add an EventSchedule object (BasicObjects > EventSchedule) at 1 -1.5 0 m and name it AppointmentTimes.
Note To move objects within the View1 window with the mouse, hold down Ctrl and click on the object with the left mouse button. Keep the mouse button down when moving the object around.
 Save your simulation.
Now add a second doctor (Process Flow > Server) at 3.5 -0.5 0 m, name it Doctor2 and give it the doctor2.png (icon made by Freepik from www.flaticon.com).
Save your simulation.
Now add a second doctor (Process Flow > Server) at 3.5 -0.5 0 m, name it Doctor2 and give it the doctor2.png (icon made by Freepik from www.flaticon.com).
 Save your simulation.
Next, add a new EntityConveyor (Process Flow > EntityConveyor) from PatientAppointment to Doctor2 as shown and update Key Inputs so that patients are generated at PatientAppointment and flow to Doctor2 across ArriveToTreat2. The EventSchedule object requires an input called TimeList which defines times in the simulation at which events occur. The EventSchedule object provides the inter-arrival times for the specified sequence of event times to the EntityGenerator object to create the entities at the specified times. In this case we want to use data from a separate file to define the appointment times so the TimeList input is left blank. Also, give Doctor2 the same treatment time as Doctor.
Save your simulation.
Next, add a new EntityConveyor (Process Flow > EntityConveyor) from PatientAppointment to Doctor2 as shown and update Key Inputs so that patients are generated at PatientAppointment and flow to Doctor2 across ArriveToTreat2. The EventSchedule object requires an input called TimeList which defines times in the simulation at which events occur. The EventSchedule object provides the inter-arrival times for the specified sequence of event times to the EntityGenerator object to create the entities at the specified times. In this case we want to use data from a separate file to define the appointment times so the TimeList input is left blank. Also, give Doctor2 the same treatment time as Doctor.
 Save your simulation.
Now we will rename the WaitingRoom Queue object to be WalkupQueue and create a new Queue object AppointmentQueue at 3.5 -1.5 0 m. Make sure to set the StateAssignment of AppointmentQueue to Wait. Set the WaitQueue for Doctor2 to be AppointmentQueue.
Next we need to duplicate the statistic gathering for the walkup patients to get similar statistics for the scheduled patients. Select the TreatToLeave EntityConveyor, right click and select Duplicate. Rename the duplicate TreatToLeave2 and adjust the y-position of its Points to be -0.5. Repeat this for the two Statistics objects to create TimeInSystem2 and WaitingTime2 at 5.5 -0.5 0 m and 6.5 -0.5 0 m respectively. Finally, repeat this for the PatientSink object (at 7.5 -0.5 0 m), but rename the two EntitySink objects to be PatientWalkupSink (the old one) and PatientAppointmentSink (the duplicate) respectively.
Save your simulation.
Now we will rename the WaitingRoom Queue object to be WalkupQueue and create a new Queue object AppointmentQueue at 3.5 -1.5 0 m. Make sure to set the StateAssignment of AppointmentQueue to Wait. Set the WaitQueue for Doctor2 to be AppointmentQueue.
Next we need to duplicate the statistic gathering for the walkup patients to get similar statistics for the scheduled patients. Select the TreatToLeave EntityConveyor, right click and select Duplicate. Rename the duplicate TreatToLeave2 and adjust the y-position of its Points to be -0.5. Repeat this for the two Statistics objects to create TimeInSystem2 and WaitingTime2 at 5.5 -0.5 0 m and 6.5 -0.5 0 m respectively. Finally, repeat this for the PatientSink object (at 7.5 -0.5 0 m), but rename the two EntitySink objects to be PatientWalkupSink (the old one) and PatientAppointmentSink (the duplicate) respectively.
 You will need to change the NextComponent Key Values of the duplicate objects as follows:
You will need to change the NextComponent Key Values of the duplicate objects as follows:
 Return to top
Return to top



