Case Study: Extended Health Clinic - With Rosters
Submitted: 6 Oct 2017
Operations Research Topics: SimulationModelling
Application Areas: Healthcare
Contents
Problem Description
This case study extends the Extended Health Clinic model. The extension adds a roster for two doctors that assigns them to the shifts involving:- only seeing Walk-up patients;
- seeing Appointment patients and Walk-up patients if free;
Problem Formulation
In order to formulate a simulation model we specify the following components:- Background – problem description
- Objectives of the study
- Expected benefits
- The CM: inputs, outputs, content, assumptions, simplifications’
- Experiments to run
- Component List
- Process flow diagram
- Logic flow diagram
- Activity cycle diagram
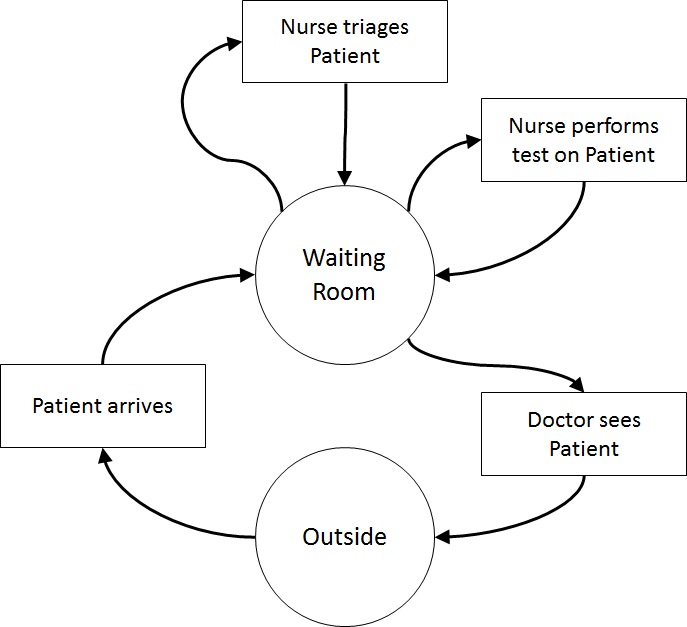
- Walk-up patients with their (inter)arrival times
- Scheduled patients with their appointment times
- Triage nurses with their triage times
- Test nurses with their testing times
- Doctors with their roster and treatment times
- Waiting room with its capacity
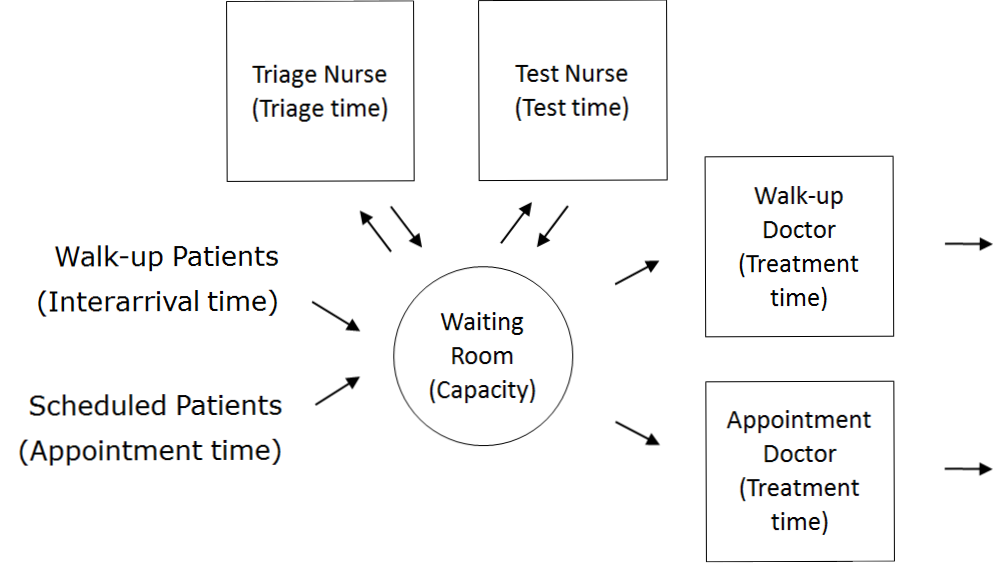
| Patient Logic Flow Diagram | Doctor Logic Flow Diagram | |
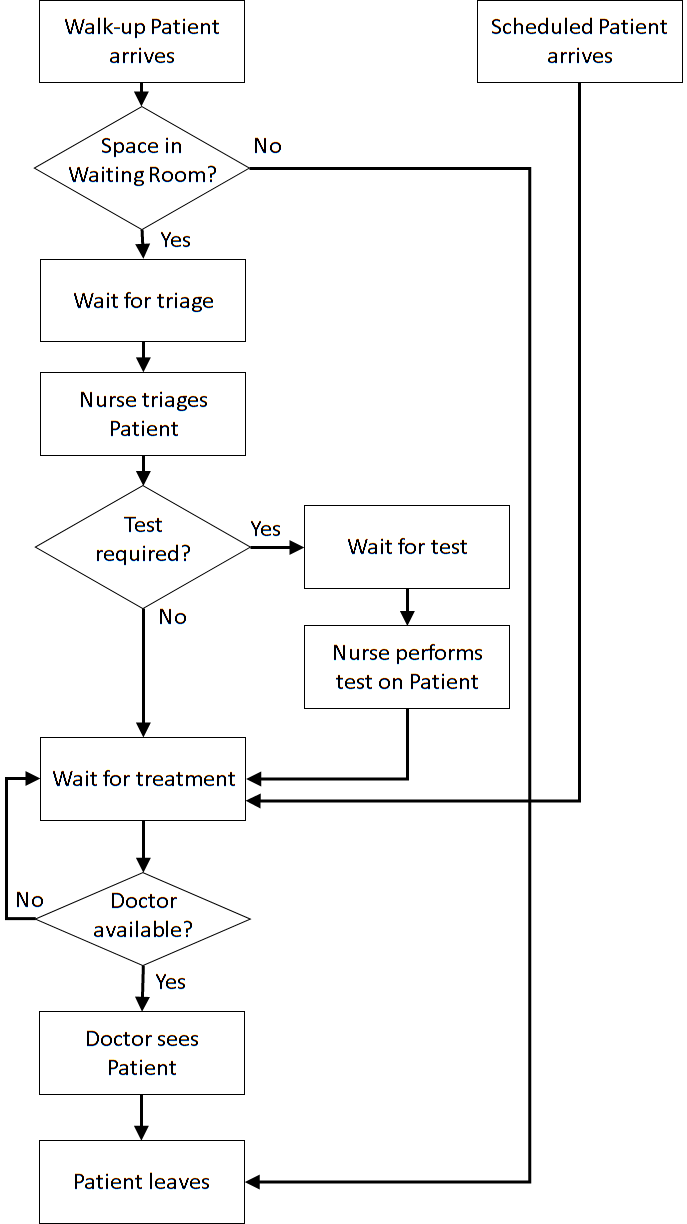 | 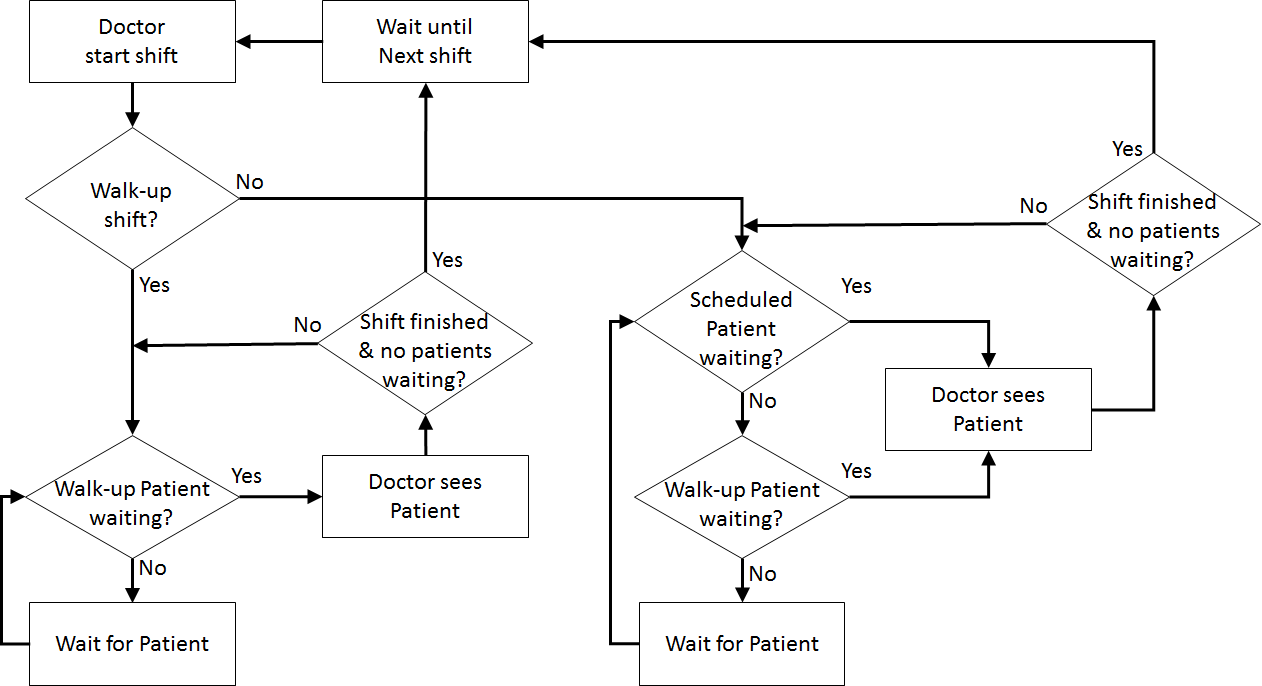 | |
| Nurse Logic Flow Diagrams | ||
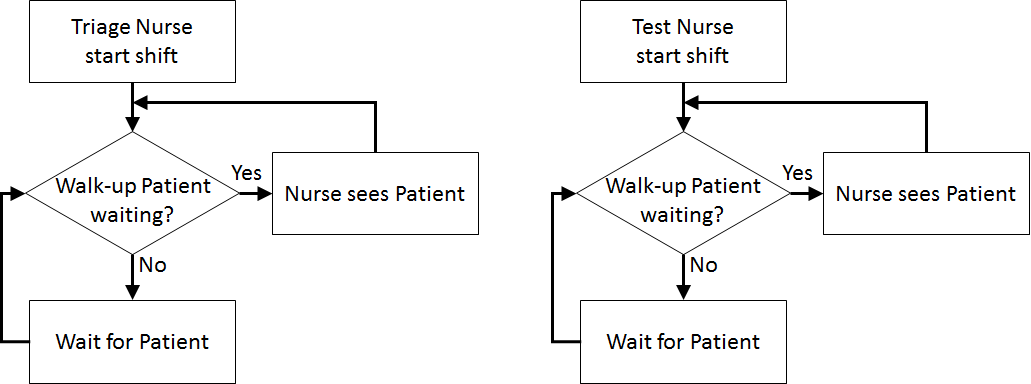 | ||
 Once the content has been established (note this is usually an iterative process) we can identify the inputs:
Once the content has been established (note this is usually an iterative process) we can identify the inputs: - doctor roster, appointment times, interarrival times, triage times, test times, treatment times;
- doctor utilisation, waiting times for triage, testing, and treatment (i.e., Patient arrives to Nurse triages Patient, Nurse triages Patient to Nurse performs test on Patient, Nurse performs test on Patient to Doctor sees Patient, Nurse triages Patient to Doctor sees Patient, Patient arrives to Doctor sees Patient), total clinic time (Patient arrives to Outside), number in waiting room.
Computational Model
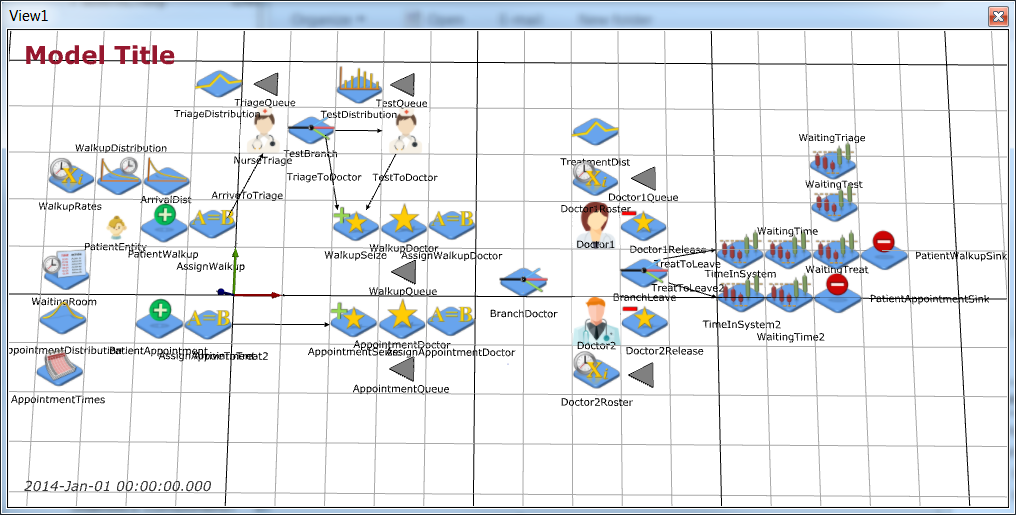
Start with the Extended Health Clinic JaamSim model. To enable the doctors to switch roles, the Server objects (that queue entities and process them one by one) need to be separated into the four distinct parts that implements a Server, namely: Resource, Seize, EntityDelay, Release.
The Resource object is used to represent a pool of identical equipment or processor units (in this case doctors). Resources can be seized and released by Seize and Release objects.
The Server object can then be modelled as a Resource with capacity one, a Seize that seizes that resource, an EntityDelay to represent the processing time, and a Release to release the resource.
However, in this example, the EntityDelay is replaced with a Server object. Strictly speaking, this is not necessary, but the Server will perform the same task as an EntityDelay since we will use the Seize and Release to control access to the Server (i.e., it won't have any queue) and it will serves the same purpose of delaying the entities for a period of time). Also, the Servers we will use have already been created (we will "repurpose them") and have useful outputs that are automatically generated, such as utilisation.
Before the new objects are created some modifications need to be made to the old model. Doctor2WalkUp, AppointmentThreshold, and WalkUpThreshold should be deleted. Note, do not delete the WalkupQueue and AppointmentQueue, we will also repurpose them later (for the Seize objects for Walk-up and Appointment patients respectively).
To enable the doctors to switch roles, the Server objects (that queue entities and process them one by one) need to be separated into the four distinct parts that implements a Server, namely: Resource, Seize, EntityDelay, Release.
The Resource object is used to represent a pool of identical equipment or processor units (in this case doctors). Resources can be seized and released by Seize and Release objects.
The Server object can then be modelled as a Resource with capacity one, a Seize that seizes that resource, an EntityDelay to represent the processing time, and a Release to release the resource.
However, in this example, the EntityDelay is replaced with a Server object. Strictly speaking, this is not necessary, but the Server will perform the same task as an EntityDelay since we will use the Seize and Release to control access to the Server (i.e., it won't have any queue) and it will serves the same purpose of delaying the entities for a period of time). Also, the Servers we will use have already been created (we will "repurpose them") and have useful outputs that are automatically generated, such as utilisation.
Before the new objects are created some modifications need to be made to the old model. Doctor2WalkUp, AppointmentThreshold, and WalkUpThreshold should be deleted. Note, do not delete the WalkupQueue and AppointmentQueue, we will also repurpose them later (for the Seize objects for Walk-up and Appointment patients respectively).
 Now rename the Doctor Server to be Doctor1 and Doctor2Appointment to be Doctor2. These Servers represent the two doctors and we will send patients to these Servers depending on what shift they are currently rostered to. First, create two new Queues Doctor1Queue and Doctor2Queue for these doctors. These queues should never be used. Next, create two Release objects (Model Builder > Process Flow > Release) that will release the Resource used by the Server once treatment has ended. Name these Release objects Doctor1Release and Doctor2Release respectively.
Now rename the Doctor Server to be Doctor1 and Doctor2Appointment to be Doctor2. These Servers represent the two doctors and we will send patients to these Servers depending on what shift they are currently rostered to. First, create two new Queues Doctor1Queue and Doctor2Queue for these doctors. These queues should never be used. Next, create two Release objects (Model Builder > Process Flow > Release) that will release the Resource used by the Server once treatment has ended. Name these Release objects Doctor1Release and Doctor2Release respectively.
 Save your simulation.
Next, we are going to create Resources to represent the (Walk-up and Appointment) shifts and create rosters for the two doctors. Add two Resources (Model Builder > Process Flow > Resource) to your model and name them AppointmentDoctor and WalkupDoctor respectively. Note that these Resources have capacity 1 by default.
Save your simulation.
Next, we are going to create Resources to represent the (Walk-up and Appointment) shifts and create rosters for the two doctors. Add two Resources (Model Builder > Process Flow > Resource) to your model and name them AppointmentDoctor and WalkupDoctor respectively. Note that these Resources have capacity 1 by default.
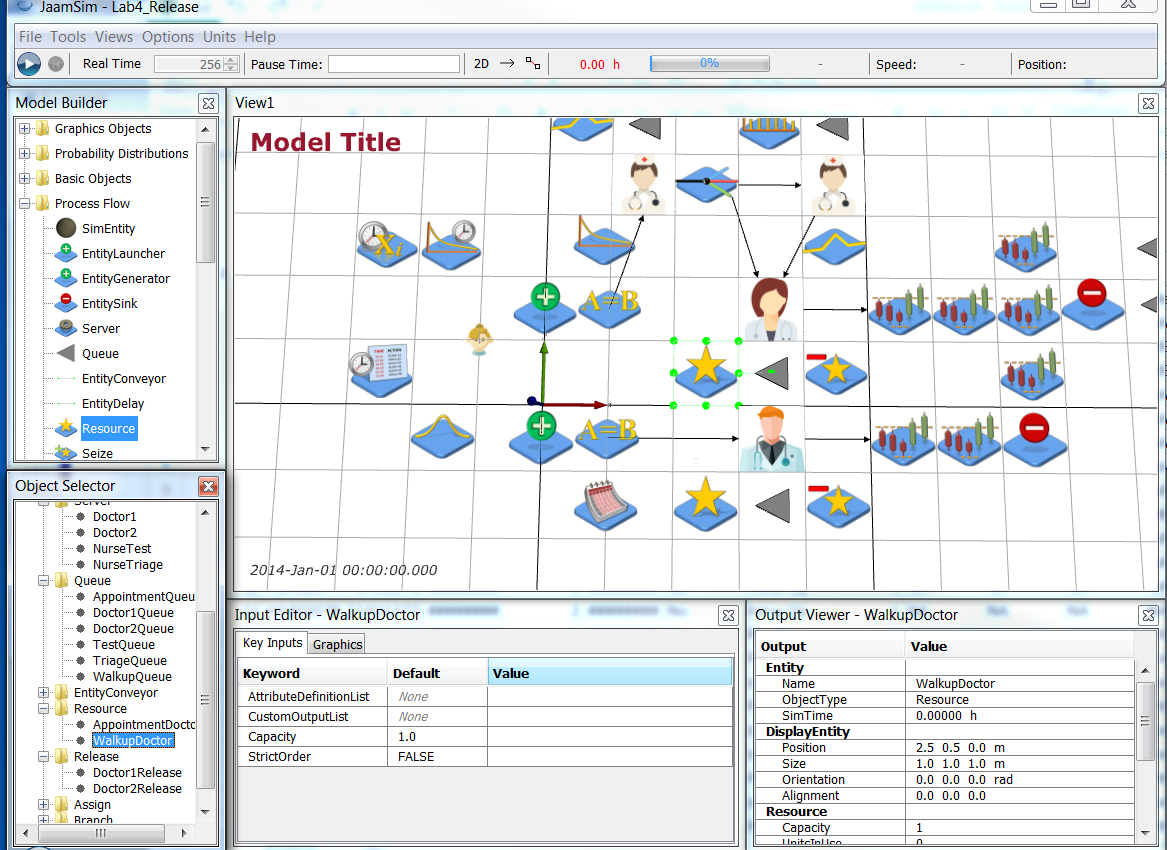 Now add two TimeSeries objects (Model Builder > Basic Objects > TimeSeries) to your model and name them Doctor1Roster and Doctor2Roster respectively. These TimeSeries define if each doctor is working as the Appointment doctor or not. Configure these TimeSeries as follows
Now add two TimeSeries objects (Model Builder > Basic Objects > TimeSeries) to your model and name them Doctor1Roster and Doctor2Roster respectively. These TimeSeries define if each doctor is working as the Appointment doctor or not. Configure these TimeSeries as follows
| Object | Key Inputs |
|---|---|
| Doctor1Roster | UnitType = DimensionlessUnit Value = { 0 h 1 } { 24 h 0 } CycleTime = 48 h |
| Doctor2Roster | UnitType = DimensionlessUnit Value = { 0 h 0 } { 24 h 1 } CycleTime = 48 h |
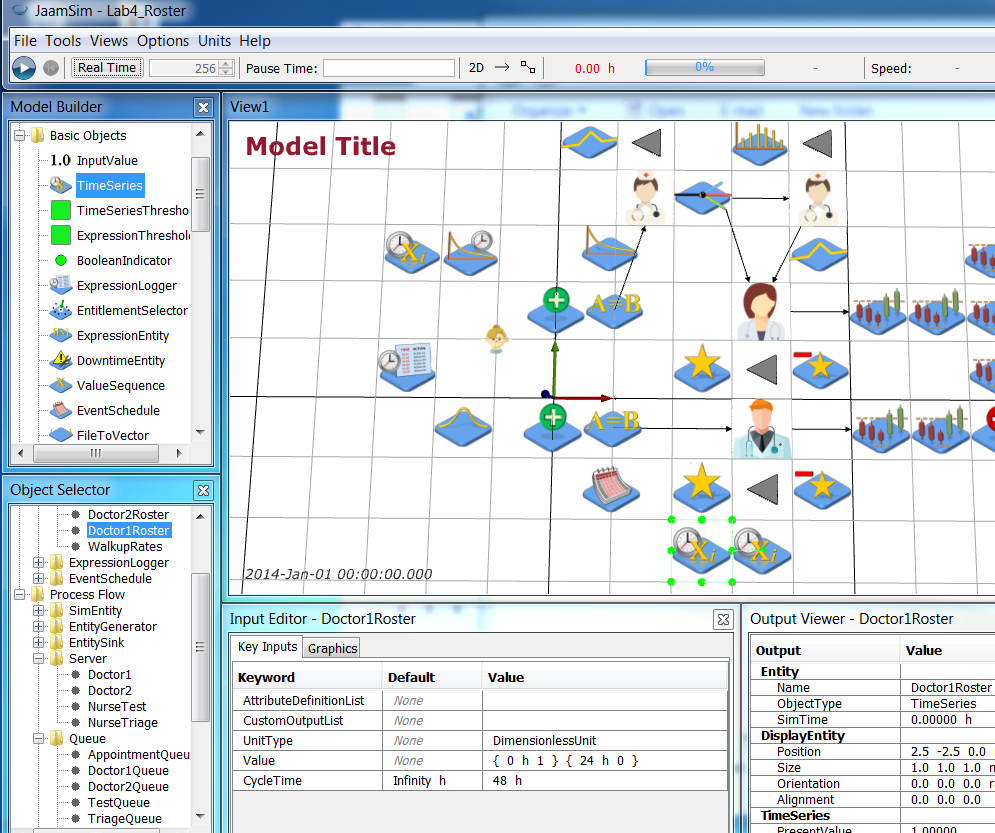 This means that Doctor1 will be the Appointment doctor for the first 24 hrs and Doctor2 will be the Appointment doctor for the next 24 hrs and this 48 hr pattern will repeat (i.e., they will alternate shifts each day).
Now reconfigure the doctor Server objects to use the new Queues, the new rosters, and send patients to the Release components. Also, we are going to generate some custom outputs
This means that Doctor1 will be the Appointment doctor for the first 24 hrs and Doctor2 will be the Appointment doctor for the next 24 hrs and this 48 hr pattern will repeat (i.e., they will alternate shifts each day).
Now reconfigure the doctor Server objects to use the new Queues, the new rosters, and send patients to the Release components. Also, we are going to generate some custom outputs
| Object | Key Inputs |
|---|---|
| Doctor1 | CustomOutputList = {DoctorNumber 1} {Queue [Doctor1Queue] } { IsAppointmentDoc [Doctor1Roster].PresentValue } NextComponent = Doctor1Release WaitQueue = Doctor1Queue |
| Doctor2 | CustomOutputList = {DoctorNumber 2} {Queue [Doctor2Queue] } { IsAppointmentDoc [Doctor2Roster].PresentValue } NextComponent = Doctor2Release WaitQueue = Doctor2Queue |
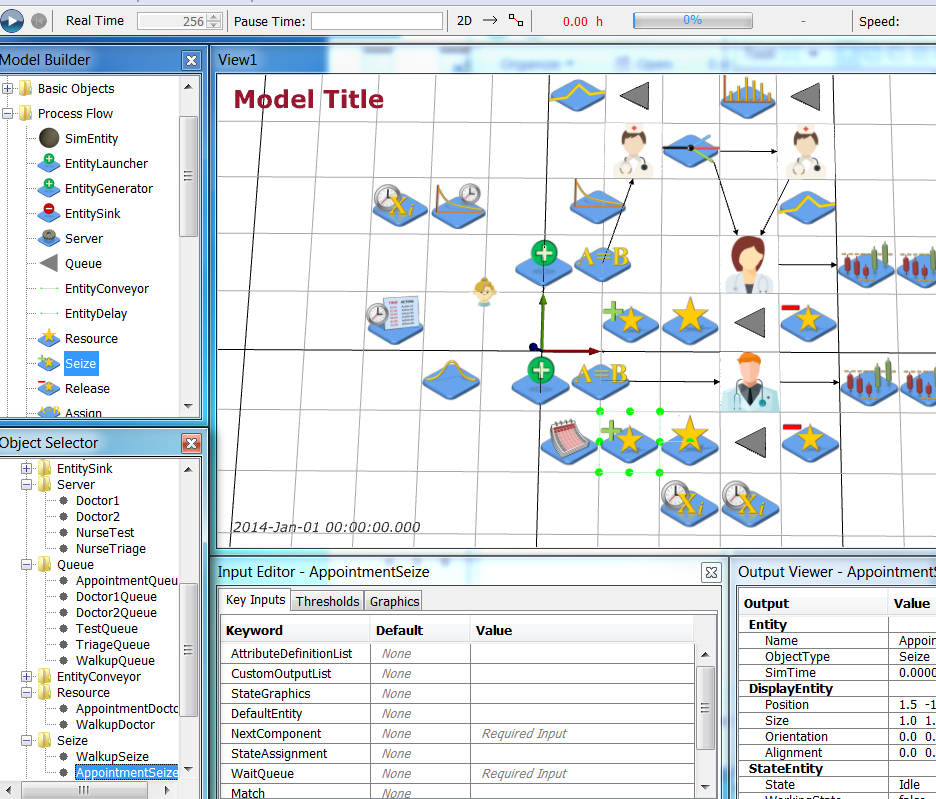 The configuration of the Seize objects is complicated and is where the majority of the logic for the doctors’ roster is implemented.
First, define a DoctorsList attribute on both Seize objects that gives the list of Servers (doctors) available to send patients to
The configuration of the Seize objects is complicated and is where the majority of the logic for the doctors’ roster is implemented.
First, define a DoctorsList attribute on both Seize objects that gives the list of Servers (doctors) available to send patients to
| Object | Key Inputs |
|---|---|
| WalkupSeize | AttributeDefinitionList = { DoctorsList '{[Doctor1], [Doctor2]}' } |
| AppointmentSeize | AttributeDefinitionList = { DoctorsList '{[Doctor1], [Doctor2]}' } |
|x|(x.IsAppointmentDoc > 0)The filter function takes this lambda function and a list of objects (in this case the DoctorsList of the Seize object), applies the function to each object in the list and then includes or excludes it from the resulting list (returned from the filter function accordingly). The NextDoc definition is
| Object | Key Inputs |
|---|---|
| AppointmentSeize | CustomOutputList = { NextDoc 'AppointmentDoc = filter(|x|(x.IsAppointmentDoc > 0), this.DoctorsList); AppointmentDoc(1)' } |
|x, y|(y.IsAppointmentDoc > x.IsAppointmentDoc)The sort function then applies this lambda function to sort the DoctorsList to create a WalkupDocs list
WalkupDocs = sort(|x, y|(y.IsAppointmentDoc > x.IsAppointmentDoc), this.DoctorsList)The WalkupDocs list is then filtered to create a list of AvailableDocs (similar to the filtering for the AppointmentSeize object) that only includes those doctor Server objects which aren’t treating patients or that have patients waiting
AvailableDocs = filter(|x|(x.NumberInProgress + x.Queue.QueueLength == 0), WalkupDocs)Note that x.Queue.QueueLength should always be zero, but JaamSim does queue patients at the doctor Servers (for zero time) before moving them into processing. Depending on the order conditional calculations are performed internally x.NumberInProgress may be 0 and x.Queue.QueueLength may be 1, hence the expression used. Finally, the first available doctor is selected for NextDoc, but WalkupSeize is sometimes checked when both doctors are treating patents, so AvailableDocs may be empty. We use a conditional statement to assign the first doctor in DoctorsList if the AvailableDocs list is empty (although the Seize will not be used by a PatientEntity as no doctor is available - so the WalkupDoctor Resource is currently utilised)
size(AvailableDocs) > 0 ? AvailableDocs(1) : this.DoctorsList(1)The final expression in its entirety is
| Object | Key Inputs |
|---|---|
| WalkupSeize | CustomOutputList = { NextDoc 'WalkupDocs = sort(|x, y|(y.IsAppointmentDoc > x.IsAppointmentDoc), this.DoctorsList); AvailableDocs = filter(|x|(x.NumberInProgress + x.Queue.QueueLength == 0), WalkupDocs); size(AvailableDocs) > 0 ? AvailableDocs(1) : this.DoctorsList(1)' } |
| Object | Key Inputs |
|---|---|
| WalkupSeize | WaitQueue = WalkupQueue ResourceList = AppointmentDoctor WalkupDoctor NumberOfUnits = { this.NextDoc.IsAppointmentDoc } { '1 - this.NextDoc.IsAppointmentDoc' } |
| AppointmentSeize | WaitQueue = AppointmentQueue ResourceList = AppointmentDoctor WalkupDoctor NumberOfUnits = { 1 } { 0 } |
| Object | Key Inputs |
|---|---|
| BranchDoctor | NextComponentList = Doctor1 Doctor2 Choice = this.obj.Doctor |
| Object | Key Inputs |
|---|---|
| AssignWalkupDoctor | AttributeAssignmentList = { 'this.obj.Doctor = [WalkupSeize].NextDoc.DoctorNumber' } { 'this.obj.SeizedDocs = [WalkupSeize].SeizedUnits' }NextComponent = BranchDoctor |
| AssignAppointmentDoctor | AttributeAssignmentList = { 'this.obj.Doctor = [AppointmentSeize].NextDoc.DoctorNumber' } { 'this.obj.SeizedDocs = [AppointmentSeize].SeizedUnits' }NextComponent = BranchDoctor |
| PatientEntity | AttributeDefinitionList = { PatientType "" } { Test 0 } { Doctor 0 } { SeizedDocs '{ 0, 0 }' } |
| Object | Key Inputs |
|---|---|
| BranchLeave | NextComponentList = TreatToLeave TreatToLeave2 Choice = 'this.obj.PatientType == "Walkup" ? 1 : 2' |
| Object | Key Inputs |
|---|---|
| TriageToDoctor | NextComponent = WalkupSeize |
| TestToDoctor | NextComponent = WalkupSeize |
| ArriveToTreat2 | NextComponent = AppointmentSeize |
| WalkupSeize | NextComponent = AssignWalkupDoctor |
| AppointmentSeize | NextComponent = AssignAppointmentDoctor |
| Doctor1Release | Resource = AppointmentDoctor WalkupDoctor NumberOfUnits = { this.obj.SeizedDocs(1) } { this.obj.SeizedDocs(2) } NextComponent = BranchLeave |
| Doctor2Release | Resource = AppointmentDoctor WalkupDoctor NumberOfUnits = { this.obj.SeizedDocs(1) } { this.obj.SeizedDocs(2) } NextComponent = BranchLeave |
 Return to top
Return to top
Results
Note that JaamSim has probably complained about your RunOutputList as we have changed a lot of components in our model and this value (Object Selector > Simulation > Key Inputs > RunOutputList) may be empty at this point. Edit the Simulation Key Inputs to get the outputs we want, the only changes are to change [Doctor].Utilisation to [Doctor1].Utilisation and'[Doctor2Appointment].Utilisation + [Doctor2Walkup].Utilisation' to [Doctor2].Utilisation.
| Object | Key Inputs |
|---|---|
| Simulation | UnitTypeList = DimensionlessUnit TimeUnit TimeUnit TimeUnit TimeUnit TimeUnit DimensionlessUnit DimensionlessUnit TimeUnit TimeUnit DimensionlessUnit DimensionlessUnit RunOutputList = { [Simulation].RunIndex(1) } { [WaitingTriage].SampleAverage } { [WaitingTest].SampleAverage } { [WaitingTreat].SampleAverage } { [WaitingTime].SampleAverage } { [TimeInSystem].SampleAverage } { '[TriageQueue].QueueLengthAverage + [TestQueue].QueueLengthAverage + [WalkupQueue].QueueLengthAverage' }{ [Doctor1].Utilisation } { [WaitingTime2].SampleAverage } { [TimeInSystem2].SampleAverage } { [AppointmentQueue].QueueLengthAverage } { [Doctor2].Utilisation } |
| Object | Multiple Runs | Value |
|---|---|---|
| Simulation | RunIndexDefinitionList | 4 100 |
| StartingRunNumber | 4-1 | |
| EndingRunNumber | 4-100 |
ConfLower Mean ConfUpper
WalkUp.WaitingTriage 0.063607 0.066832 0.070057
WalkUp.WaitingTest 0.001793 0.001953 0.002113
WalkUp.WaitingTreat 0.127544 0.135612 0.143679
WalkUp.WaitingTime 0.194155 0.204397 0.214640
WalkUp.TimeInSystem 0.709928 0.720624 0.731319
Num.WalkUps.Waiting 0.469415 0.497684 0.525952
Doctor1.Utilisation 0.641166 0.645107 0.649047
Appointment.WaitingTime 0.194093 0.200859 0.207624
Appointment.TimeInSystem 0.476982 0.484046 0.491111
Appointment.Queue 0.572599 0.593162 0.613724
Doctor2.Utilisation 0.692690 0.696761 0.700831
> t.test(Lab4scen$WalkUp.WaitingTime, Lab4scen$Appointment.WaitingTime)
Welch Two Sample t-test
data: Lab4scen$WalkUp.WaitingTime and Lab4scen$Appointment.WaitingTime
t = 0.572, df = 171.57, p-value = 0.5681
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.008672611 0.015749916
sample estimates:
mean of x mean of y
0.2043972 0.2008585
|
> t.test(Lab4scen$WalkUp.TimeInSystem, Lab4scen$Appointment.TimeInSystem)
Welch Two Sample t-test
data: Lab4scen$WalkUp.TimeInSystem and Lab4scen$Appointment.TimeInSystem
t = 36.621, df = 171.57, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.2238259 0.2493289
sample estimates:
mean of x mean of y
0.7206239 0.4840465
|
> t.test(Lab4scen$Num.WalkUps.Waiting, Lab4scen$Appointment.Queue)
Welch Two Sample t-test
data: Lab4scen$Num.WalkUps.Waiting and Lab4scen$Appointment.Queue
t = -5.4196, df = 180.85, p-value = 1.889e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.13023947 -0.06071654
sample estimates:
mean of x mean of y
0.4976837 0.5931617
|
> t.test(Lab4scen$Doctor1.Utilisation, Lab4scen$Doctor2.Utilisation)
Welch Two Sample t-test
data: Lab4scen$Doctor1.Utilisation and Lab4scen$Doctor2.Utilisation
t = -18.092, df = 197.79, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.05728439 -0.04602373
sample estimates:
mean of x mean of y
0.6451066 0.6967607
|
> t.test(Lab3scen$WalkUp.WaitingTime, Lab3scen$Appointment.WaitingTime)
Welch Two Sample t-test
data: Lab3scen$WalkUp.WaitingTime and Lab3scen$Appointment.WaitingTime
t = 15.837, df = 107.4, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1069441 0.1375463
sample estimates:
mean of x mean of y
0.2509337 0.1286884
|
> t.test(Lab3scen$WalkUp.TimeInSystem, Lab3scen$Appointment.TimeInSystem)
Welch Two Sample t-test
data: Lab3scen$WalkUp.TimeInSystem and Lab3scen$Appointment.TimeInSystem
t = 44.681, df = 109.6, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3385983 0.3700297
sample estimates:
mean of x mean of y
0.7660578 0.4117439
|
> t.test(Lab3scen$Num.WalkUps.Waiting, Lab3scen$Appointment.Queue)
Welch Two Sample t-test
data: Lab3scen$Num.WalkUps.Waiting and Lab3scen$Appointment.Queue
t = 11.073, df = 110.3, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1892095 0.2716937
sample estimates:
mean of x mean of y
0.6122041 0.3817525
|
> t.test(Lab3scen$Doctor.Utilisation, Lab3scen$Doctor2.Utilisation)
Welch Two Sample t-test
data: Lab3scen$Doctor.Utilisation and Lab3scen$Doctor2.Utilisation
t = -113.6, df = 159.57, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.3491496 -0.3372173
sample estimates:
mean of x mean of y
0.4993517 0.8425352
|
| Object | Key Inputs |
|---|---|
| WalkupQueue | Priority = 2 |
| AppointmentQueue | Priority = 1 |
> t.test(Lab4scen$WalkUp.WaitingTime, Lab4scen$Appointment.WaitingTime)
Welch Two Sample t-test
data: Lab4scen$WalkUp.WaitingTime and Lab4scen$Appointment.WaitingTime
t = 15.715, df = 107.83, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1064297 0.1371549
sample estimates:
mean of x mean of y
0.2520324 0.1302401
|
> t.test(Lab4scen$WalkUp.TimeInSystem, Lab4scen$Appointment.TimeInSystem)
Welch Two Sample t-test
data: Lab4scen$WalkUp.TimeInSystem and Lab4scen$Appointment.TimeInSystem
t = 44.444, df = 110.04, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3384345 0.3700247
sample estimates:
mean of x mean of y
0.7679160 0.4136864
|
> t.test(Lab4scen$Num.WalkUps.Waiting, Lab4scen$Appointment.Queue)
Welch Two Sample t-test
data: Lab4scen$Num.WalkUps.Waiting and Lab4scen$Appointment.Queue
t = 11.03, df = 110.76, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.1888664 0.2715930
sample estimates:
mean of x mean of y
0.6140961 0.3838663
|
> t.test(Lab4scen$Doctor1.Utilisation, Lab4scen$Doctor2.Utilisation)
Welch Two Sample t-test
data: Lab4scen$Doctor1.Utilisation and Lab4scen$Doctor2.Utilisation
t = -16.645, df = 197.12, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.05411466 -0.04265012
sample estimates:
mean of x mean of y
0.6467522 0.6951346
|
Conclusions
In this case study, you extended the Extended Health Clinic model to use a roster for the doctors in order to try and balance workload. You investigated the effect of this change to the quality of care of the patients (their experience was the same as before) as well as the workload of the doctors. The workload seems fairly (but not exactly) balanced over 168 hrs. Return to top| I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
Lab4Analysis.R | r1 | manage | 1.2 K | 2017-10-08 - 09:26 | MichaelOSullivan |
This topic: OpsRes > SubmitCaseStudy > EHCWithRosters
Topic revision: r8 - 2019-10-07 - MichaelOSullivan
Ideas, requests, problems regarding TWiki? Send feedback

