Case Study: The American Steel Transshipment Problem
Submitted: 15 Feb 2008
Operations Research Topics:
Application Areas: Logistics
Contents
Problem Description
THE AMERICAN STEEL PROBLEM
American Steel, an Ohio-based steel manufacturing company, produces steel at its two steel mills located at Youngstown and Pittsburgh. The company distributes finished steel to its retail customers through the distribution network of regional and field warehouses shown below:
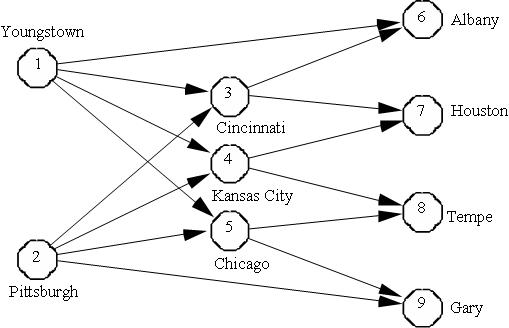
The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the
cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
| From node |
To node |
Cost |
Minimum |
Maximum |
| Youngstown |
Albany |
500 |
- |
1000 |
| Youngstown |
Cincinnati |
350 |
- |
3000 |
| Youngstown |
Kansas City |
450 |
1000 |
5000 |
| Youngstown |
Chicago |
375 |
- |
5000 |
| Pittsburgh |
Cincinnati |
350 |
- |
2000 |
| Pittsburgh |
Kansas City |
450 |
2000 |
3000 |
| Pittsburgh |
Chicago |
400 |
- |
4000 |
| Pittsburgh |
Gary |
450 |
- |
2000 |
| Cincinnati |
Albany |
350 |
1000 |
5000 |
| Cincinnati |
Houston |
550 |
- |
6000 |
| Kansas City |
Houston |
375 |
- |
4000 |
| Kansas City |
Tempe |
650 |
- |
4000 |
| Chicago |
Tempe |
600 |
- |
2000 |
| Chicago |
Gary |
120 |
- |
4000 |
The current monthly demand at American Steel’s four field warehouses is as follows:
| Field Warehouses |
Monthly Demand |
| Albany, N.Y. |
3000 |
| Houston |
7000 |
| Tempe |
4000 |
| Gary |
6000 |
The Youngstown and Pittsburgh mills can produce up to 10,000 tons and 15,000 tons of steel per month, respectively. The management wants to know the least cost monthly shipment plan.
Return to top
Problem Formulation
1. IDENTIFY THE DECISION VARIABLES
The decision variables for this problem are the same as for the transportation problem, the
Flow of goods (cases of beer in The Beer Distribution Problem, tons of steels here) through the network. In <span style=
Return to top
Computational Model
The computational model...
Return to top
Results
Implementing the usual script file with
transshipment.mod and
steel.dat (with the
Cost modification) gives us the optimal
Flow variables:
<img width=
Return to top
Conclusions
There is quite a bit of information to summarise and many ways to present it. Some suggestions include:
- Summarise the problem as usual and list the shipments that American Steel should make (similar to the transportation problem);
- Summarise the problem as usual and present a table of shipments that American Steel should make;
- Draw the network formulation for the problem (being sure to specify what the labels mean). Then draw the actual solution on top of the network formulation. You could colour code flows long arcs to show if they are at their bounds.
Implementation and Ongoing Monitoring
Given that the solution is very sensitive to the supply and demand amounts, careful consideration of the accuracy of these figures is important. Making sure that the bounds on the arcs are reliable is another concern.
Ongoing monitoring of the supply, demand and bounds will help American Steel to keep making good decisions. As shown in the parametric analysis, ongoing negotiation of transportation prices along important routes will help American Steel reduce their expenditure.
Return to top
Extra for Experts
Another common network flow problem that uses almost the same model as transshipment is the
maximum flow problem. The objective of this problem is to maximise flow through the network. The only changes to
transshipment.mod are:
- A new variable
FlowOut is introduced at each node;
-
FlowOut has lower and upper bounds, often the upper bound is set to as the Demand at the nodes;
-
FlowOut replaces Demand in the ConserveFlow constraints;
- The
ConserveFlow constraint becomes an equality constraint as all flow must be accounted for (no storage at the nodes);
-
Cost of transshipment is ignored;
- The objective is to maximise the total flow out of the network
sum {n in NODES} FlowOut[n];
- The problem no longer needs to be balanced.
Maxflow.mod
<span style=
Return to top
Student Tasks
- Solve The American Steel Problem. Write a management summary of your solution.
What to hand in Hand in your management summary.
EXTRA FOR EXPERTS' TASKS
- American Steel are planning a marketing campaign to increase demand in their four markets Albany, Tempe, Houston and Gary. However, they would like to know the maximum demand their distribution network can handle (in each market) before they proceed. Write a script file that uses
maxflow.mod and steel.dat to find the maximum demand they can supply in each market.
What to hand in Hand in your script file and a management summary of your solution.
Return to top
 The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.
The network represents shipment of finished steel from American Steel’s two steel mills located at Youngstown (node 1) and Pittsburgh (node 2) to their field warehouses at Albany, Houston, Tempe, and Gary (nodes 6, 7, 8 and 9) through three regional warehouses located at Cincinnati, Kansas City, and Chicago (nodes 3, 4 and 5). Also, some field warehouses can be directly supplied from the steel mills.
The table below presents the minimum and maximum flow amounts of steel that may be shipped between different cities along with the cost per 1000 ton/month of shipping the steel. For example, the shipment from Youngstown to Kansas City is contracted out to a railroad company with a minimal shipping clause of 1000 tons/month. However, the railroad cannot ship more then 5000 tons/month due the shortage of rail cars.



