
Difference: VariablesInAMPL (5 vs. 6)
Revision 62009-07-21 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> Variables in AMPL | ||||||||
| Line: 22 to 22 | ||||||||
Declaring a VariableAMPL variables are created by using thevar keyword and a label for the variable: | ||||||||
| Changed: | ||||||||
| < < | var <varname>; | |||||||
| > > | var ; | |||||||
Example | ||||||||
| Changed: | ||||||||
| < < | var x1; | |||||||
| > > | var x1; | |||||||
| Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: | ||||||||
| Changed: | ||||||||
| < < |
var <varname> [{<indexname>}];
| |||||||
| > > | var [{}]; | |||||||
Example | ||||||||
| Changed: | ||||||||
| < < |
var Percentage {INGREDIENTS};
You can access the variable corresponding to the member of a set by using brackets [ and ]
let Price['Malibu'] := 100; solve; display Price['Malibu]':or you can access all the variables at once by using the variable name display Price; | |||||||
| > > | var Percentage {INGREDIENTS};
You can access the variable corresponding to the member of a set by using brackets [ and ]
let Price['Malibu'] := 100; solve; display Price['Malibu']:or you can access all the variables at once by using the variable name display Price; | |||||||
Return to top
Variable TypesVariables must be one of four types: real (the default),binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). | ||||||||
| Changed: | ||||||||
| < < | var <varname> [<type>]; | |||||||
| > > | var []; | |||||||
Examples | ||||||||
| Changed: | ||||||||
| < < |
var Build binary;
var Production {SURFBOARDS} integer;
| |||||||
| > > | var Build binary; var Production {SURFBOARDS} integer; | |||||||
| Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a mixed-integer (non)linear programme and is often more difficult to solve. | ||||||||
| Changed: | ||||||||
| < < | Symbolic variables are used to restrict a variable to lie within a set, e.g,
set VOWELS := {'a', 'e', 'i', 'o', 'u'};
var vowel symbolic in VOWELS;
so the in <setname> must follow the =symbolic keyword. | |||||||
| > > | Symbolic variables are used to restrict a variable to lie within a set, e.g.,
set VOWELS := {'a', 'e', 'i', 'o', 'u'};var vowel symbolic in VOWELS;so the in must follow the symbolic keyword. | |||||||
Return to top
Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g., | ||||||||
| Changed: | ||||||||
| < < |
var Percentage {INGREDIENTS} >= 0;
var Production {SURFBOARDS} integer >= 0;
| |||||||
| > > | var Percentage {INGREDIENTS} >= 0;var Production {SURFBOARDS} integer >= 0; | |||||||
| Bounds are set by adding them after the variable label: | ||||||||
| Changed: | ||||||||
| < < | var <varname> [>= <lb>] [<= <ub>];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas.
var Percentage {INGREDIENTS} <= 0, >= 100;
var Production {SURFBOARDS} integer >= 0;
| |||||||
| > > | var [>= ] [<= ];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. var Percentage {INGREDIENTS} <= 0, >= 100;var Production {SURFBOARDS} integer >= 0; | |||||||
Return to top
Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator:= and the required initial value. | ||||||||
| Changed: | ||||||||
| < < | var Price := 1;To set an initial value dynamically use the let keyword with the assignment operator and required value before solving.
var Price {SURFBOARDS};
let Price['Malibu'] := 1;
let Price['SuperThruster'] := 1;
option solver minos;
solve;
| |||||||
| > > | var Price := 1;To set an initial value dynamically use the let keyword with the assignment operator and required value before solving. var Price {SURFBOARDS};let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; | |||||||
Return to top
Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using thedefault keyword. | ||||||||
| Changed: | ||||||||
| < < |
var Price {SURFBOARDS} >= 0 default 100;
| |||||||
| > > | var Price {SURFBOARDS} >= 0 default 100; | |||||||
| You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value. | ||||||||
| Changed: | ||||||||
| < < |
var Price {SURFBOARDS} >= 0 default 1;
let Price['Super Thruster'] := 50;
solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50
| |||||||
| > > | var Price {SURFBOARDS} >= 0 default 1;let Price['Super Thruster'] := 50; solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50 | |||||||
Return to top
Accessing a Variable | ||||||||
| Changed: | ||||||||
| < < | Variable values are accessed by specifying the indices of the variable you want to access within [ and ]. | |||||||
| > > | Variable values are accessed by specifying the indices of the variable you want to access within [ and ]. | |||||||
ExamplesSeeAmount below. | ||||||||
| Changed: | ||||||||
| < < |
# Objective: minimise the cost per (100g) can
minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Amount[i];
# Constraints: Meet the nutritional requirements
subject to MeetRequirement {r in REQUIREMENTS}:
Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r];
| |||||||
| > > | # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Amount[i];# Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r]; | |||||||
| Return to top | ||||||||
| Line: 161 to 95 | ||||||||
You can easily examine the value of a variable using the display command. You can also examine the column of a variable by using the expand keyword. | ||||||||
| Changed: | ||||||||
| < < | 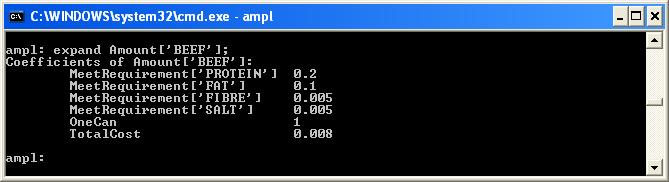 | |||||||
| > > |  | |||||||
| Return to top | ||||||||
| Line: 170 to 104 | ||||||||
Once variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value.
To fix a variable, use the fix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | fix <name>; | |||||||
| > > | fix ; | |||||||
If you decide that the variable should be considered again, you can unfix the variable.
To stop a variable being fixed, use the unfix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | unfix <name>; | |||||||
| > > | unfix ; | |||||||
Consider the Surfboard Production Problem we can fix the Price variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. | ||||||||
| Changed: | ||||||||
| < < |
param Objective {1..150, 1..150};
fix Price;
for {p in 1..150 by 1, q in 1..150 by 1} {
let Price['Malibu'] := p;
let Price['Super Thruster'] := q;
option solver cplex;
solve;
let Objective[p, q] := TotalProfit;
}
| |||||||
| > > | param Objective {1..150, 1..150};fix Price; for {p in 1..150 by 1, q in 1..150 by 1} {let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } | |||||||
| We can also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. | ||||||||
| Changed: | ||||||||
| < < | reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; | |||||||
| > > | reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; | |||||||
| Return to top | ||||||||
View topic | History: r8 < r7 < r6 < r5 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback