
Difference: VariablesInAMPL (1 vs. 8)
Revision 82011-09-16 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> Variables in AMPL | ||||||||
| Line: 63 to 63 | ||||||||
Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. var Percentage {INGREDIENTS} <= 0, >= 100;var Production {SURFBOARDS} integer >= 0; | ||||||||
| Added: | ||||||||
| > > | Parameters as BoundsTo use parameters as bounds you first need to define the parameters, then use them when defining the variable, By using defaults you only need to define bounds when necessary:
param lb {FEEDS} default 0; # Could use -Infinity here
param ub {FEEDS} default Infinity;
var Amount {f in FEEDS} >= lb[f] <= ub[f]; # Amount[f] >= 0 for all f by default
data;
param lb :=
GRAIN 1
;
param ub :=
GRAIN 10
PASTURE 6
;
# The amount of grain is between 1 and 10, the amoun tof pasture is <= 6, all amounts are >= 0
| |||||||
Return to top
Initial Values | ||||||||
Revision 72009-10-09 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> Variables in AMPL | ||||||||
| Line: 22 to 22 | ||||||||
Declaring a VariableAMPL variables are created by using thevar keyword and a label for the variable: | ||||||||
| Changed: | ||||||||
| < < | var ; | |||||||
| > > | var <varname>; | |||||||
Examplevar x1;Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: | ||||||||
| Changed: | ||||||||
| < < | var [{}]; | |||||||
| > > | var <varname> [{<set>}]; | |||||||
Examplevar Percentage {INGREDIENTS}; | ||||||||
| Line: 41 to 41 | ||||||||
Variable TypesVariables must be one of four types: real (the default),binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). | ||||||||
| Changed: | ||||||||
| < < | var []; | |||||||
| > > | var <varname> [<type>]; | |||||||
Examplesvar Build binary; var Production {SURFBOARDS} integer; | ||||||||
| Line: 59 to 59 | ||||||||
var Percentage {INGREDIENTS} >= 0;var Production {SURFBOARDS} integer >= 0;
Bounds are set by adding them after the variable label: | ||||||||
| Changed: | ||||||||
| < < | var [>= ] [<= ];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. var Percentage {INGREDIENTS} <= 0, >= 100;var Production {SURFBOARDS} integer >= 0; | |||||||
| > > | var <varname> [>= <lb>] [<= <ub>];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. var Percentage {INGREDIENTS} <= 0, >= 100;var Production {SURFBOARDS} integer >= 0; | |||||||
| Return to top | ||||||||
| Line: 75 to 77 | ||||||||
Another way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using the default keyword.
var Price {SURFBOARDS} >= 0 default 100; | ||||||||
| Changed: | ||||||||
| < < | You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value. | |||||||
| > > | You can still change the initial value of the variables using the let keyword, but if you don't they will automatically take on the default value. | |||||||
var Price {SURFBOARDS} >= 0 default 1;let Price['Super Thruster'] := 50; solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50Return to top | ||||||||
| Line: 104 to 106 | ||||||||
Once variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value.
To fix a variable, use the fix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | fix ; | |||||||
| > > | fix <varname>; | |||||||
If you decide that the variable should be considered again, you can unfix the variable.
To stop a variable being fixed, use the unfix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | unfix ; | |||||||
| > > | unfix <varname>; | |||||||
Consider the Surfboard Production Problem we can fix the Price variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables.
param Objective {1..150, 1..150};fix Price; for {p in 1..150 by 1, q in 1..150 by 1} {let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } | ||||||||
Revision 62009-07-21 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> Variables in AMPL | ||||||||
| Line: 22 to 22 | ||||||||
Declaring a VariableAMPL variables are created by using thevar keyword and a label for the variable: | ||||||||
| Changed: | ||||||||
| < < | var <varname>; | |||||||
| > > | var ; | |||||||
Example | ||||||||
| Changed: | ||||||||
| < < | var x1; | |||||||
| > > | var x1; | |||||||
| Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: | ||||||||
| Changed: | ||||||||
| < < |
var <varname> [{<indexname>}];
| |||||||
| > > | var [{}]; | |||||||
Example | ||||||||
| Changed: | ||||||||
| < < |
var Percentage {INGREDIENTS};
You can access the variable corresponding to the member of a set by using brackets [ and ]
let Price['Malibu'] := 100; solve; display Price['Malibu]':or you can access all the variables at once by using the variable name display Price; | |||||||
| > > | var Percentage {INGREDIENTS};
You can access the variable corresponding to the member of a set by using brackets [ and ]
let Price['Malibu'] := 100; solve; display Price['Malibu']:or you can access all the variables at once by using the variable name display Price; | |||||||
Return to top
Variable TypesVariables must be one of four types: real (the default),binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). | ||||||||
| Changed: | ||||||||
| < < | var <varname> [<type>]; | |||||||
| > > | var []; | |||||||
Examples | ||||||||
| Changed: | ||||||||
| < < |
var Build binary;
var Production {SURFBOARDS} integer;
| |||||||
| > > | var Build binary; var Production {SURFBOARDS} integer; | |||||||
| Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a mixed-integer (non)linear programme and is often more difficult to solve. | ||||||||
| Changed: | ||||||||
| < < | Symbolic variables are used to restrict a variable to lie within a set, e.g,
set VOWELS := {'a', 'e', 'i', 'o', 'u'};
var vowel symbolic in VOWELS;
so the in <setname> must follow the =symbolic keyword. | |||||||
| > > | Symbolic variables are used to restrict a variable to lie within a set, e.g.,
set VOWELS := {'a', 'e', 'i', 'o', 'u'};var vowel symbolic in VOWELS;so the in must follow the symbolic keyword. | |||||||
Return to top
Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g., | ||||||||
| Changed: | ||||||||
| < < |
var Percentage {INGREDIENTS} >= 0;
var Production {SURFBOARDS} integer >= 0;
| |||||||
| > > | var Percentage {INGREDIENTS} >= 0;var Production {SURFBOARDS} integer >= 0; | |||||||
| Bounds are set by adding them after the variable label: | ||||||||
| Changed: | ||||||||
| < < | var <varname> [>= <lb>] [<= <ub>];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas.
var Percentage {INGREDIENTS} <= 0, >= 100;
var Production {SURFBOARDS} integer >= 0;
| |||||||
| > > | var [>= ] [<= ];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. var Percentage {INGREDIENTS} <= 0, >= 100;var Production {SURFBOARDS} integer >= 0; | |||||||
Return to top
Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator:= and the required initial value. | ||||||||
| Changed: | ||||||||
| < < | var Price := 1;To set an initial value dynamically use the let keyword with the assignment operator and required value before solving.
var Price {SURFBOARDS};
let Price['Malibu'] := 1;
let Price['SuperThruster'] := 1;
option solver minos;
solve;
| |||||||
| > > | var Price := 1;To set an initial value dynamically use the let keyword with the assignment operator and required value before solving. var Price {SURFBOARDS};let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; | |||||||
Return to top
Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using thedefault keyword. | ||||||||
| Changed: | ||||||||
| < < |
var Price {SURFBOARDS} >= 0 default 100;
| |||||||
| > > | var Price {SURFBOARDS} >= 0 default 100; | |||||||
| You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value. | ||||||||
| Changed: | ||||||||
| < < |
var Price {SURFBOARDS} >= 0 default 1;
let Price['Super Thruster'] := 50;
solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50
| |||||||
| > > | var Price {SURFBOARDS} >= 0 default 1;let Price['Super Thruster'] := 50; solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50 | |||||||
Return to top
Accessing a Variable | ||||||||
| Changed: | ||||||||
| < < | Variable values are accessed by specifying the indices of the variable you want to access within [ and ]. | |||||||
| > > | Variable values are accessed by specifying the indices of the variable you want to access within [ and ]. | |||||||
ExamplesSeeAmount below. | ||||||||
| Changed: | ||||||||
| < < |
# Objective: minimise the cost per (100g) can
minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Amount[i];
# Constraints: Meet the nutritional requirements
subject to MeetRequirement {r in REQUIREMENTS}:
Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r];
| |||||||
| > > | # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Amount[i];# Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r]; | |||||||
| Return to top | ||||||||
| Line: 161 to 95 | ||||||||
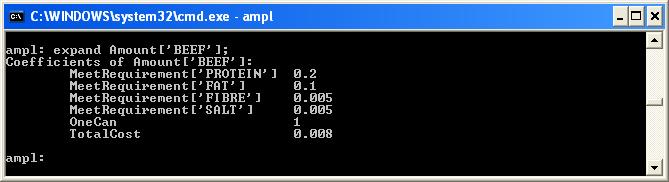
You can easily examine the value of a variable using the display command. You can also examine the column of a variable by using the expand keyword. | ||||||||
| Changed: | ||||||||
| < < |  | |||||||
| > > |  | |||||||
| Return to top | ||||||||
| Line: 170 to 104 | ||||||||
Once variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value.
To fix a variable, use the fix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | fix <name>; | |||||||
| > > | fix ; | |||||||
If you decide that the variable should be considered again, you can unfix the variable.
To stop a variable being fixed, use the unfix keyword and the variable name. | ||||||||
| Changed: | ||||||||
| < < | unfix <name>; | |||||||
| > > | unfix ; | |||||||
Consider the Surfboard Production Problem we can fix the Price variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. | ||||||||
| Changed: | ||||||||
| < < |
param Objective {1..150, 1..150};
fix Price;
for {p in 1..150 by 1, q in 1..150 by 1} {
let Price['Malibu'] := p;
let Price['Super Thruster'] := q;
option solver cplex;
solve;
let Objective[p, q] := TotalProfit;
}
| |||||||
| > > | param Objective {1..150, 1..150};fix Price; for {p in 1..150 by 1, q in 1..150 by 1} {let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } | |||||||
| We can also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. | ||||||||
| Changed: | ||||||||
| < < | reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; | |||||||
| > > | reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; | |||||||
| Return to top | ||||||||
Revision 52008-03-02 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Ready to Review --> Variables in AMPL | ||||||||
| Line: 32 to 32 | ||||||||
| Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: | ||||||||
| Added: | ||||||||
| > > |
var <varname> [{<indexname>}];
| |||||||
Example | ||||||||
| Line: 149 to 152 | ||||||||
| # Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: | ||||||||
| Changed: | ||||||||
| < < | Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r]; | |||||||
| > > | Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i] <= Max[r]; | |||||||
| Return to top | ||||||||
Revision 42008-03-02 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
| Changed: | ||||||||
| < < | <-- Under Construction --> | |||||||
| > > | <-- Ready to Review --> | |||||||
Variables in AMPL | ||||||||
Revision 32008-02-29 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Under Construction --> | ||||||||
| Added: | ||||||||
| > > | Variables in AMPL | |||||||
| Changed: | ||||||||
| < < |
DescriptionAMPL variables are used to represent variables in mathematical programmes. They are quantities that a solver (e.g., CPLEX, MINOS) is allowed to change as it looks for a solution to the mathematical programme. Declaring a VariableAMPL variables are created by using the {\tt var} keyword and a label for the variable: \begin{verbatim} var \end{verbatim} Example\begin{verbatim} var x1; \end{verbatim} Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: Example\begin{verbatim} var Percentage {INGREDIENTS}; \end{verbatim} You can access the variable corresponding to the member of a set by using brackets {\tt [} and {\tt ]} \begin{verbatim} let Price['Malibu'] := 100; solve; display Price['Malibu]': \end{verbatim} or you can access all the variables at once by using the variable name \begin{verbatim} display Price; \end{verbatim} Variable TypesVariables must be one of four types: real (the default), binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). \begin{verbatim} var \end{verbatim} Examples\begin{verbatim} var Build binary; var Production {SURFBOARDS} integer; \end{verbatim} Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a _mixed-integer (non)linear programme_ and is often more difficult to solve. Symbolic variables are used to restrict a variable to lie within a set, e.g, \begin{verbatim} set VOWELS := {'a', 'e', 'i', 'o', 'u'}; var vowel symbolic in VOWELS; \end{verbatim} so the {\tt in Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g. \begin{verbatim} var Percentage {INGREDIENTS} >= 0; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Bounds are set by adding them after the variable label: \begin{verbatim} var \end{verbatim} **Note** There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. \begin{verbatim} var Percentage {INGREDIENTS} >= 0, <= 100; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator {\tt :=} and the required initial value. \begin{verbatim} var Price := 1; \end{verbatim} To set an initial value dynamically use the {\tt let} keyword with the assignment operator and required value before solving. \begin{verbatim} var Price {SURFBOARDS}; let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; \end{verbatim} Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using the {\tt default} keyword. \begin{verbatim} var Price {SURFBOARDS} >= 0 default 100; \end{verbatim} You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value. \begin{verbatim} var Price {SURFBOARDS} >= 0 default 1; let Price['Super Thruster'] := 50; solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50 \end{verbatim} Accessing a VariableVariable values are accessed by specifying the indices of the variable you want to access within {\tt [} and {\tt ]}. ExamplesSee {\tt Percentage} below. \begin{verbatim} # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Percentage[i]; # Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Percentage[i] <= Max[r]; \end{verbatim} Examining VariablesYou can easily examine the value of a variable using the {\tt display} command. You can also examine the column of a variable by using the {\tt expand} keyword.  Fixing ValuesOnce variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value. To fix a variable, use the {\tt fix} keyword and the variable name. \begin{verbatim} fix \end{verbatim} If you decide that the variable should be considered again, you can unfix the variable. To stop a variable being fixed, use the {\tt unfix} keyword and the variable name. \begin{verbatim} unfix \end{verbatim} In The Surfboard Production Problem we fix the {\tt Price} variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. \begin{verbatim} param Objective {1..150, 1..150}; fix Price; for {p in 1..150 by 1, q in 1..150 by 1} { let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } \end{verbatim} We also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. \begin{verbatim} reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; \end{verbatim} | |||||||
| > > |
DescriptionAMPL variables are used to represent variables in mathematical programmes. They are quantities that a solver (e.g., CPLEX, MINOS) is allowed to change as it looks for a solution to the mathematical programme. Return to topDeclaring a VariableAMPL variables are created by using thevar keyword and a label for the variable:
var <varname>; Examplevar x1;Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: Example
var Percentage {INGREDIENTS};
You can access the variable corresponding to the member of a set by using brackets [ and ]
let Price['Malibu'] := 100; solve; display Price['Malibu]':or you can access all the variables at once by using the variable name display Price;Return to top Variable TypesVariables must be one of four types: real (the default),binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable).
var <varname> [<type>]; Examples
var Build binary;
var Production {SURFBOARDS} integer;
Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a mixed-integer (non)linear programme and is often more difficult to solve.
Symbolic variables are used to restrict a variable to lie within a set, e.g,
set VOWELS := {'a', 'e', 'i', 'o', 'u'};
var vowel symbolic in VOWELS;
so the in <setname> must follow the =symbolic keyword.
Return to top
Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g.,
var Percentage {INGREDIENTS} >= 0;
var Production {SURFBOARDS} integer >= 0;
Bounds are set by adding them after the variable label:
var <varname> [>= <lb>] [<= <ub>];Note There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas.
var Percentage {INGREDIENTS} <= 0, >= 100;
var Production {SURFBOARDS} integer >= 0;
Return to top
Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator:= and the required initial value.
var Price := 1;To set an initial value dynamically use the let keyword with the assignment operator and required value before solving.
var Price {SURFBOARDS};
let Price['Malibu'] := 1;
let Price['SuperThruster'] := 1;
option solver minos;
solve;
Return to top
Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using thedefault keyword.
var Price {SURFBOARDS} >= 0 default 100;
You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value.
var Price {SURFBOARDS} >= 0 default 1;
let Price['Super Thruster'] := 50;
solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50
Return to top
Accessing a VariableVariable values are accessed by specifying the indices of the variable you want to access within[ and ].
ExamplesSeeAmount below.
# Objective: minimise the cost per (100g) can
minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Amount[i];
# Constraints: Meet the nutritional requirements
subject to MeetRequirement {r in REQUIREMENTS}:
Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Amount[i]
Return to top
Examining VariablesYou can easily examine the value of a variable using thedisplay command. You can also examine the column of a variable by using the expand keyword.
 Return to top
Return to top
Fixing ValuesOnce variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value. To fix a variable, use thefix keyword and the variable name.
fix <name>;If you decide that the variable should be considered again, you can unfix the variable. To stop a variable being fixed, use the unfix keyword and the variable name.
unfix <name>;Consider the Surfboard Production Problem we can fix the Price variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables.
param Objective {1..150, 1..150};
fix Price;
for {p in 1..150 by 1, q in 1..150 by 1} {
let Price['Malibu'] := p;
let Price['Super Thruster'] := q;
option solver cplex;
solve;
let Objective[p, q] := TotalProfit;
}
We can also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution.
reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production;Return to top | |||||||
| -- MichaelOSullivan - 28 Feb 2008 \ No newline at end of file | ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 22008-02-28 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
<-- Under Construction --> | ||||||||
| Changed: | ||||||||
| < < |
DescriptionAMPL variables are used to represent variables in mathematical programmes. They are quantities that a solver (e.g., CPLEX, MINOS) is allowed to change as it looks for a solution to the mathematical programme. Declaring a VariableAMPL variables are created by using the {\tt var} keyword and a label for the variable: \begin{verbatim} var \end{verbatim} Example\begin{verbatim} var x1; \end{verbatim} Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: Example\begin{verbatim} var Percentage {INGREDIENTS}; \end{verbatim} You can access the variable corresponding to the member of a set by using brackets {\tt [} and {\tt ]} \begin{verbatim} let Price['Malibu'] := 100; solve; display Price['Malibu]': \end{verbatim} or you can access all the variables at once by using the variable name \begin{verbatim} display Price; \end{verbatim} Variable TypesVariables must be one of four types: real (the default), binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). \begin{verbatim} var \end{verbatim} Examples\begin{verbatim} var Build binary; var Production {SURFBOARDS} integer; \end{verbatim} Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a mixed-integer (non)linear programme and is often more difficult to solve. Symbolic variables are used to restrict a variable to lie within a set, e.g, \begin{verbatim} set VOWELS := {'a', 'e', 'i', 'o', 'u'}; var vowel symbolic in VOWELS; \end{verbatim} so the {\tt in <setname>} must follow the {\tt symbolic} keyword. We don't use symbolic variables in our case studies. Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g. \begin{verbatim} var Percentage {INGREDIENTS} >= 0; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Bounds are set by adding them after the variable label: \begin{verbatim} var \end{verbatim} **Note** There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. \begin{verbatim} var Percentage {INGREDIENTS} >= 0, <= 100; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator {\tt :=} and the required initial value. \begin{verbatim} var Price := 1; \end{verbatim} To set an initial value dynamically use the {\tt let} keyword with the assignment operator and required value before solving. \begin{verbatim} var Price {SURFBOARDS}; let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; \end{verbatim} Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using the {\tt default} keyword. \begin{verbatim}
\begin{verbatim}
ExamplesSee {\tt Percentage} below. \begin{verbatim} # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Percentage[i]; # Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Percentage[i] <= Max[r]; \end{verbatim} Examining VariablesYou can easily examine the value of a variable using the {\tt display} command. You can also examine the column of a variable by using the {\tt expand} keyword.  Fixing ValuesOnce variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value. To fix a variable, use the {\tt fix} keyword and the variable name. \begin{verbatim} fix \end{verbatim} If you decide that the variable should be considered again, you can unfix the variable. To stop a variable being fixed, use the {\tt unfix} keyword and the variable name. \begin{verbatim} unfix \end{verbatim} In The Surfboard Production Problem we fix the {\tt Price} variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. \begin{verbatim} param Objective {1..150, 1..150}; fix Price; for {p in 1..150 by 1, q in 1..150 by 1} { let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } \end{verbatim} We also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. \begin{verbatim} reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; \end{verbatim} | |||||||
| > > |
DescriptionAMPL variables are used to represent variables in mathematical programmes. They are quantities that a solver (e.g., CPLEX, MINOS) is allowed to change as it looks for a solution to the mathematical programme. Declaring a VariableAMPL variables are created by using the {\tt var} keyword and a label for the variable: \begin{verbatim} var \end{verbatim} Example\begin{verbatim} var x1; \end{verbatim} Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: Example\begin{verbatim} var Percentage {INGREDIENTS}; \end{verbatim} You can access the variable corresponding to the member of a set by using brackets {\tt [} and {\tt ]} \begin{verbatim} let Price['Malibu'] := 100; solve; display Price['Malibu]': \end{verbatim} or you can access all the variables at once by using the variable name \begin{verbatim} display Price; \end{verbatim} Variable TypesVariables must be one of four types: real (the default), binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). \begin{verbatim} var \end{verbatim} Examples\begin{verbatim} var Build binary; var Production {SURFBOARDS} integer; \end{verbatim} Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a _mixed-integer (non)linear programme_ and is often more difficult to solve. Symbolic variables are used to restrict a variable to lie within a set, e.g, \begin{verbatim} set VOWELS := {'a', 'e', 'i', 'o', 'u'}; var vowel symbolic in VOWELS; \end{verbatim} so the {\tt in Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g. \begin{verbatim} var Percentage {INGREDIENTS} >= 0; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Bounds are set by adding them after the variable label: \begin{verbatim} var \end{verbatim} **Note** There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. \begin{verbatim} var Percentage {INGREDIENTS} >= 0, <= 100; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator {\tt :=} and the required initial value. \begin{verbatim} var Price := 1; \end{verbatim} To set an initial value dynamically use the {\tt let} keyword with the assignment operator and required value before solving. \begin{verbatim} var Price {SURFBOARDS}; let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; \end{verbatim} Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using the {\tt default} keyword. \begin{verbatim} var Price {SURFBOARDS} >= 0 default 100; \end{verbatim} You can still change the initial value of the variables using the {\tt let} keyword, but if you don't they will automatically take on the default value. \begin{verbatim} var Price {SURFBOARDS} >= 0 default 1; let Price['Super Thruster'] := 50; solve; # Price['Malibu'] starts at 100, Price['Super Thruster'] starts at 50 \end{verbatim} Accessing a VariableVariable values are accessed by specifying the indices of the variable you want to access within {\tt [} and {\tt ]}. ExamplesSee {\tt Percentage} below. \begin{verbatim} # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Percentage[i]; # Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Percentage[i] <= Max[r]; \end{verbatim} Examining VariablesYou can easily examine the value of a variable using the {\tt display} command. You can also examine the column of a variable by using the {\tt expand} keyword.  Fixing ValuesOnce variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value. To fix a variable, use the {\tt fix} keyword and the variable name. \begin{verbatim} fix \end{verbatim} If you decide that the variable should be considered again, you can unfix the variable. To stop a variable being fixed, use the {\tt unfix} keyword and the variable name. \begin{verbatim} unfix \end{verbatim} In The Surfboard Production Problem we fix the {\tt Price} variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. \begin{verbatim} param Objective {1..150, 1..150}; fix Price; for {p in 1..150 by 1, q in 1..150 by 1} { let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } \end{verbatim} We also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. \begin{verbatim} reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; \end{verbatim} | |||||||
| -- MichaelOSullivan - 28 Feb 2008 \ No newline at end of file | ||||||||
Revision 12008-02-28 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Added: | ||||||||
| > > |
<-- Under Construction -->
DescriptionAMPL variables are used to represent variables in mathematical programmes. They are quantities that a solver (e.g., CPLEX, MINOS) is allowed to change as it looks for a solution to the mathematical programme. Declaring a VariableAMPL variables are created by using the {\tt var} keyword and a label for the variable: \begin{verbatim} var \end{verbatim} Example\begin{verbatim} var x1; \end{verbatim} Often, you will want to create one variable for every member (respectively pair, tuple) from a set (a two-dimensional set, multi-dimensional set, respectively). To do this you simply add the set after the variable name: Example\begin{verbatim} var Percentage {INGREDIENTS}; \end{verbatim} You can access the variable corresponding to the member of a set by using brackets {\tt [} and {\tt ]} \begin{verbatim} let Price['Malibu'] := 100; solve; display Price['Malibu]': \end{verbatim} or you can access all the variables at once by using the variable name \begin{verbatim} display Price; \end{verbatim} Variable TypesVariables must be one of four types: real (the default), binary (0-1), integer or symbolic. You declare the type of a variable by adding the type keyword after the variable label (or giving no type if it is a real variable). \begin{verbatim} var \end{verbatim} Examples\begin{verbatim} var Build binary; var Production {SURFBOARDS} integer; \end{verbatim} Real variables can take any real value, binary variables must be either 0 (often meaning false) or 1 (often meaning true), and integer variables can take on any integer value. If a mathematical programme has any binary or integer variables then it is a mixed-integer (non)linear programme and is often more difficult to solve. Symbolic variables are used to restrict a variable to lie within a set, e.g, \begin{verbatim} set VOWELS := {'a', 'e', 'i', 'o', 'u'}; var vowel symbolic in VOWELS; \end{verbatim} so the {\tt in <setname>} must follow the {\tt symbolic} keyword. We don't use symbolic variables in our case studies. Variable BoundsBoth real and integer variables may have lower and upper bounds. For example, in many mathematical programmes variables are assumed to be nonnegative, e.g. \begin{verbatim} var Percentage {INGREDIENTS} >= 0; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Bounds are set by adding them after the variable label: \begin{verbatim} var \end{verbatim} **Note** There are many attributes that may follow a variable declaration. They can be placed in any order and must be separated by either whitespace or commas. \begin{verbatim} var Percentage {INGREDIENTS} >= 0, <= 100; var Production {SURFBOARDS} integer >= 0; \end{verbatim} Initial ValuesOften (especially when solving a nonlinear programme) the initial value, i.e., the value the variable has at the start of the solution process, will affect how the mathematical programme solves. In AMPL you can set initial values on variables either when you declare them or dynamically. To set an initial value within a variable declaration simply add an assignment operator {\tt :=} and the required initial value. \begin{verbatim} var Price := 1; \end{verbatim} To set an initial value dynamically use the {\tt let} keyword with the assignment operator and required value before solving. \begin{verbatim} var Price {SURFBOARDS}; let Price['Malibu'] := 1; let Price['SuperThruster'] := 1; option solver minos; solve; \end{verbatim} Default ValuesAnother way of setting initial variable values is to set a new default value (otherwise AMPL sets variables to 0 by default). This is done using the {\tt default} keyword. \begin{verbatim}
\begin{verbatim}
ExamplesSee {\tt Percentage} below. \begin{verbatim} # Objective: minimise the cost per (100g) can minimize TotalCost: sum {i in INGREDIENTS} Cost[i] * Percentage[i]; # Constraints: Meet the nutritional requirements subject to MeetRequirement {r in REQUIREMENTS}: Min[r] <= sum {i in INGREDIENTS} Contributes[i, r] * Percentage[i] <= Max[r]; \end{verbatim} Examining VariablesYou can easily examine the value of a variable using the {\tt display} command. You can also examine the column of a variable by using the {\tt expand} keyword.  Fixing ValuesOnce variables have been added to a model you cannot remove them. However, you can set their values and fix them so that their value doesn't change. AMPL will then treat that variable as a parameter with the fixed value. To fix a variable, use the {\tt fix} keyword and the variable name. \begin{verbatim} fix \end{verbatim} If you decide that the variable should be considered again, you can unfix the variable. To stop a variable being fixed, use the {\tt unfix} keyword and the variable name. \begin{verbatim} unfix \end{verbatim} In The Surfboard Production Problem we fix the {\tt Price} variables to remove their nonlinearity. This allows us to use CPLEX to find the optimal production levels for different prices and explore the nonlinear objective function of the price variables. \begin{verbatim} param Objective {1..150, 1..150}; fix Price; for {p in 1..150 by 1, q in 1..150 by 1} { let Price['Malibu'] := p; let Price['Super Thruster'] := q; option solver cplex; solve; let Objective[p, q] := TotalProfit; } \end{verbatim} We also fix the prices to their rounded values (to the nearest cent) and re-solve to see what effect the rounding has on the solution. \begin{verbatim} reset; model surfboard.mod; data surfboard.dat; option solver cplex; let Price['Malibu'] := 100; let Price['Super Thruster'] := 58.14; fix Price; solve; display Price, Production; \end{verbatim} -- MichaelOSullivan - 28 Feb 2008 | |||||||
Ideas, requests, problems regarding TWiki? Send feedback