Case Study: Calibrating the Courier Service Model
Submitted: 27 Sep 2009
Application Areas: Logistics
Contents
Problem Description
This case study extends two previous case studies:
- Modelling Requests to a Courier Service which builds a model of a courier service receiving requests and then making deliveries;
- Input and Output for a Courier Service Model which uses Arena tools (the Input Analyzer and Output Analyzer) to find distributions for the input to the simulation model and compares the results for fitted distributions vs empirical distributions.
In this case study we will build a simulation that uses historical data directly (instead of within an empirical distribution). Using this simulation we can estimate the total time between a request for delivery arriving at the courier service and the delivery being made.
Once we have an accurate value for the actual time a delivery request takes be be delivered, we can calibrate our fitted distributions to accurately match the real-world situation.
First, we will use
Arena's Process Analyzer to simultaneously compare several different possibilities for the fitted distribution using the uniform error in the estimate of average total time (i.e., the time between a delivery request arriving and the delivery being made). Then, we will use
Arena's OptQuest to find the best parameters for the distributions of choice by minimising the uniform error in the estimate. Finally, we will add the optimised simulation to the comparison in the Process Analyzer.
Return to top
Problem Formulation
We can easily modify the existing Courier Service Model to use the data in
courier.xls because both the arrival of delivery requests and the delivery runs themselves have been abstracted into submodels.
To use the historical data to generate arrivals we simply need to step through the interarrival times for both the Inner City and Metropolitan delivery request, wait the required time and generate the appropriate arrival.
To use the historical data to implement delivery runs we until a delivery run is triggered (either by the number of deliveries waiting being large enough or the time since the first undelivered request being long enough) and then use the next delivery run time from the list as the time taken for the courier to make a delivery run.
The historical data simulation gives us a "real-world" value for the average time between a delivery request arriving and the corresponding delivery being made. We can use this "actual" value to calculate the uniform error in estimates of average total time
To calibrate our simulation we need to minimise
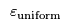
by changing the parameters to our fitted distributions. We can use black-box optimisation, in this case Tabu search via
Arena's OptQuest, to determine the values of the fitted distribution parameters that provide the minimum uniform error.
Return to top
Computational Model
First, we need to name each of the relevant columns of the
courier.xls spreadsheet. The attached
flash
movie shows how to name a column in an Excel 2007 spreadsheet.
Naming Columns in courier.xls
Once all four columns have been named:
inner_city_interarrivals;
metropolitan_arrivals;
inner_city_deliveries;
metropolitan_deliveries; save a copy of your spreadsheet as
courier-named.xls.
Now, add this file to your courier service simulation using the
File data module (in the
Advanced Process template).
| Name |
Historical Data |
| Access Type |
Microsoft Excel (*.xls) |
| Operating System File Name |
<your directory> \courier-named.xls |
Once the file has been added we use the names defined in courier-named.xls to define
Recordsets.
Adding Recordsets to a File module
| Recordsets (secondary dialog via Recordsets button) |
| |
Recordset Name |
Inner City Interarrivals |
| |
Named Range |
inner_city_interarrivals |
| |
Recordset Name |
Metropolitan Interarrivals |
| |
Named Range |
metropolitan_interarrivals |
| |
Recordset Name |
Inner City Deliveries |
| |
Named Range |
inner_city_deliveries |
| |
Recordset Name |
Metropolitan Deliveries |
| |
Named Range |
metropolitan_deliveries |
Now our historical data is available for use in our simulation.
It is easiest to use the data from courier-named.xls for delivery runs first.
Getting Delivery Times from Historical Data
| Name |
Read Inner City Delivery Time |
| Type |
Read from File |
| Arena File Name |
Historical |
| Recordset ID |
Inner City Deliveries |
| Assignments (secondary dialog via Add button) |
| |
Type |
Attribute |
| |
Attribute Name |
DeliveryTime |
| Name |
Make Inner City Delivery Run |
| Delay Type |
Expression |
| Units |
Minutes |
| Expression |
DeliveryTime |
Using the historical data to generate arrivals is more complicated as we need to create entities according to the historical data. We do this by creating a logical entity in a loop. This entity is created at the start of the replication, reads the data, delays for the specified time, creates an entity (via a
Separate module) and then loops back to reading the data.
Getting Interarrival Times from Historical Data
| Name |
Create Inner City Request Generator |
| Entity Type |
RequestGenerator |
| Max Arrivals |
1 |
| Name |
Read Inner City Interarrival Time |
| Type |
Read from File |
| Arena File Name |
Historical |
| Recordset ID |
Inner City Interarrivals |
| Assignments (secondary dialog via Add button) |
| |
Type |
Attribute |
| |
Attribute Name |
InterarrivalTime |
| Name |
Wait till Inner City Arrival |
| Delay Time |
InterarrivalTime |
| Units |
Minutes |
| Name |
Make Inner City Delivery |
| Name |
Make Inner City Request Entity |
| Assignments (secondary dialog via Add button) |
| |
Type |
Entity Type |
| |
Entity Type |
InnerCityRequest |
Now we have a simulation that uses historical data. However, we need to see how long we can use the historical data before it repeats (Arena goes back to the start of a Recordset when it runs out of data). If we sum each of the columns in courier-names.xls and convert it from minutes into 8-hour days, we see that the Inner City Deliveries data (the time between Inner City delivery requests) provides just over 30 days of data. All the other columns provide enough data fro longer durations. We set the number of replications for the historical data simulation to be 30, with each replication running for 8 hours.
| Number of Replications |
30 |
| Replication Length |
8 |
| Time Units |
Hours |
Return to top
Results
Now we have a historical simulation, we can run the simulation and look at statistics from the real-world courier service.
Figure 1 shows the
Category Overview report with total time for both Inner City and Metropolitan deliveries, averaged over the 30 replications.
Figure 1 Total Time from the Historical Simulation

Comparing Multiple Simulations
First, we will use the
Process Analyzer to compare the historical simulation with both the simulation with fitted distributions and the simulation with empirical distributions. First, add the three simulation models to the
Process Analyzer.
Adding Simulations to the Process Analyzer
Then, select all the simulations and run them using the
Go button

.
IMPORTANT. You should set all the simulations (historical, fitted distributions, empirical distributions) to run in batch mode. You can do this by selecting
Run > Run Control > Batch Run (No Animation). To make sure the simulations run file is properly set up for the
Process Analyzer you should run it once with all the settings you want to use in the
Process Analyzer, e.g., as a batch run, 50 replications, etc.
Running the Process Analyzer
After all the simulations have run in the
Process Analyzer, we can compare the total time for both Inner City and Metropolitan deliveries by inserting responses into the
Process Analyzer. After the responses have been inserted, we can use Box-and-Whisker plots to compare the confidence intervals for the total time from all the simulations simultaneously.
Making Box-and-Whisker Plots
The box in the Box-and-Whisker plots shows the 95% confidence interval and both the fitted and the empirical distributions give confidence intervals that overlap with the historical simulation confidence intervals for Inner City and Metropolitan total delivery time. However, we can use optimisation to further calibrate the distributions to see if we have the best distribution parameters.
Changing Distribution Parameters
We want to experiment with different distribution values for the fitted distributions. The current distributions are:
| Inner City Interarrivals |
EXPO(4.38) |
| Metropolitan Interarrivals |
GAMM(10.3, 1.37) |
| Inner City Delivery |
15 + 4 * BETA(4.28, 5.95) |
| Metropolitan Delivery |
11 + GAMM(6.4, 4.49) |
In order to change these values dynamically we need to parameterise the distributions. Add the following variables to the
Variable data module:
| Name |
Inner City Lambda |
| Initial Values |
4.38 |
| Name |
Metropolitan Alpha |
| Initial Values |
10.3 |
| Name |
Metropolitan Beta |
| Initial Values |
1.37 |
| Name |
Inner City Delivery Constant |
| Initial Values |
15 |
| Name |
Inner City Delivery Multiplier |
| Initial Values |
4 |
| Name |
Inner City Delivery Beta1 |
| Initial Values |
4.28 |
| Name |
Inner City Delivery Beta2 |
| Initial Values |
5.95 |
| Name |
Metropolitan Delivery Constant |
| Initial Values |
11 |
| Name |
Metropolitan Delivery Alpha |
| Initial Values |
6.4 |
| Name |
Metropolitan Delivery Beta |
| Initial Values |
4.49 |
and use them to define the appropriate distributions
| Name |
Generate Inner City Delivery |
| Expression |
EXPO(Inner City Lambda) |
| First Creation |
EXPO(Inner City Lambda) |
| Name |
Generate Metropolitan Delivery |
| Expression |
GAMM(Metropolitan Alpha, Metropolitan Beta) |
| First Creation |
GAMM(Metropolitan Alpha, Metropolitan Beta) |
| Name |
Make Inner City Delivery Run |
| Delay Type |
Expression |
| Units |
Minutes |
| Expression |
Inner City Delivery Constant + Inner City Delivery Multiplier * BETA(Inner City Delivery Beta1, Inner City Delivery Beta2) |
| Name |
Make Metropolitan Delivery Run |
| Delay Type |
Expression |
| Units |
Minutes |
| Expression |
Metropolitan Delivery Constant + GAMM(Metropolitan Delivery Alpha, Metropolitan Delivery Beta) |
Now run this simulation for 50 replication in batch mode to create the simulation run file. Next, create a new
Process Analyzer file with the historical simulation, and 3 copies of the parameterised fitted distribution, i.e., 4 scenarios in all. Add the total time in the system for both Inner City deliveries and Metropolitan deliveries (see
Figure 2).
Now, we want to add the distribution parameters as controls so we can experiment with them (see
Figure 2). We will see what happens when we increase and decrease the arrival rate for the Inner City delivery requests. Change the values for
Inner City Lambda in the two experimental scenarios to be 4 and 4.5 respectively. Then run these scenarios. After running these scenraios you should get the results shown in
Figure 2.
Figure 2 Using controls to the
Process Analyzer

It is not clear from our experiments if decreasing or increasing the arrival rate for Inner City delivery requests will give a better "match" for the total time to deliver both Inner City and Metropolitan requests.To fully explore the possibilities for the fitted distributions we will minimise the uniform error using OptQuest.
Minimising Uniform Error via OptQuest
The "actual" values for the total delivery time is 23.216 minutes for an Inner City request and 49.529 for a Metropolitan request. We can use these values along with our parameterised model and OptQuest to find the best overall fit to the historical data. Rather than use the absolute value for the uniform error, we calculate the squared uniform error for both Inner City deliveries and Metropolitan deliveries and use the sum of these values. This squared sum will hopefully provide the Tabu search with better impetus to find the minimum uniform error (if the solution is far from the minimum error, the squared error will be much greater than the absolute error).
OptQuest for Courier Service Calibration
After 119 simulation runs in OptQuest, the optimisation terminates with best values for the parameters:
Inner City Lambda |
4.266820 |
Metropolitan Alpha |
10.294055 |
Metropolitan Beta |
0.5 |
Inner City Delivery Constant |
15 |
Inner City Delivery Multiplier |
3.854484 |
Inner City Delivery Beta1 |
3.992073 |
Inner City Delivery Beta2 |
6.345527 |
Metropolitan Delivery Constant |
10.484961 |
Metropolitan Delivery Alpha |
6.967382 |
Metropolitan Delivery Beta |
4.257940 |
and checking the Box-and-Whisker plot (see
Figure 3) for the new parameters shows a much improved match to the historical simulation.
Figure 3 Box-andWhisker plot for Optimised Parameters

The total times for both an Inner City delivery and a Metropolitan delivery seem to match better, although given that all the confidence intervals overlap, there is most likely no statistical evidence of a difference between the 3 simulation models. Increasing the number of replications (i.e., increasing accuracy) may uncover any difference. Note that
Metropolitan Beta is at its lower bound. This indicates that the lower bound used in OptQuest may have been too restrictive and we should set these higher and optimise again.
Return to top
Conclusions
In this case study we have used historical data and optimisation to calibrate our simulation model. The historical data was used within our simulation model to get actual values for the total time for courier deliveries.
Once these actual values were calculated, we compared to our previous models, showing a reasonable match. We used optimisation (via OptQuest) to see if better parameter values for the distributions previously fitted to the historical data (in
Input and Output for a Courier Service Model).
The calibrated fitted model was then compared to the simulation model with historical data and the match was seemed improved, although further simulation work and statistical analysis is needed to confirm this.
Return to top

 It is not clear from our experiments if decreasing or increasing the arrival rate for Inner City delivery requests will give a better "match" for the total time to deliver both Inner City and Metropolitan requests.To fully explore the possibilities for the fitted distributions we will minimise the uniform error using OptQuest.
It is not clear from our experiments if decreasing or increasing the arrival rate for Inner City delivery requests will give a better "match" for the total time to deliver both Inner City and Metropolitan requests.To fully explore the possibilities for the fitted distributions we will minimise the uniform error using OptQuest.
 The total times for both an Inner City delivery and a Metropolitan delivery seem to match better, although given that all the confidence intervals overlap, there is most likely no statistical evidence of a difference between the 3 simulation models. Increasing the number of replications (i.e., increasing accuracy) may uncover any difference. Note that
The total times for both an Inner City delivery and a Metropolitan delivery seem to match better, although given that all the confidence intervals overlap, there is most likely no statistical evidence of a difference between the 3 simulation models. Increasing the number of replications (i.e., increasing accuracy) may uncover any difference. Note that 


