
Difference: DepthFirstSearch (3 vs. 4)
Revision 42008-05-07 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Line: 12 to 12 | ||||||||
reset; | ||||||||
| Changed: | ||||||||
| < < | model cutting_stock.mod; data cutting_stock.dat; | |||||||
| > > | model cutting_stock_col.mod; data cutting_stock_col.dat; param TotalLength; param Length {ROLLS} >= 0; data; param TotalLength := 20; param Length := A 5 B 7 C 9 ; model; | |||||||
| reset data PatternYield, PATTERNS; # Remove any pattern data, we will find it automatically # Search the possibilities for cutting patterns | ||||||||
| Changed: | ||||||||
| < < | param MinLength := min {i in ITEMS} Length[i]; # Find the minimum length of all the items param MaxPossible {i in ITEMS} >= 0, integer # Find the maximum number of each length item | |||||||
| > > | param MinLength := min {i in ROLLS} Length[i]; # Find the minimum length of all the ROLLS param MaxPossible {i in ROLLS} >= 0, integer # Find the maximum number of each length item | |||||||
| := TotalLength div Length[i]; # that can be cut from a roll # The current product being considered | ||||||||
| Changed: | ||||||||
| < < | param current symbolic within ITEMS; | |||||||
| > > | param current symbolic within ROLLS; | |||||||
| # The number of each product being cut | ||||||||
| Changed: | ||||||||
| < < | param number {ITEMS} >= 0, integer, default 0; | |||||||
| > > | param number {ROLLS} >= 0, integer, default 0; | |||||||
| # Are we still searching? param stillSearching binary; | ||||||||
| Line: 33 to 48 | ||||||||
| param newPattern > 0, integer; let PATTERNS := {}; | ||||||||
| Changed: | ||||||||
| < < | # Start with the first product and no items being cut let current := first(ITEMS); | |||||||
| > > | # Start with the first product and no ROLLS being cut let current := first(ROLLS); | |||||||
| let number[current] := 0; let stillSearching := 1; repeat { display current, number; | ||||||||
| Changed: | ||||||||
| < < | if ( current <> last(ITEMS) ) and | |||||||
| > > | if ( current <> last(ROLLS) ) and | |||||||
| ( number[current] <= MaxPossible[current] ) then { | ||||||||
| Changed: | ||||||||
| < < | let current := next(current, ITEMS); | |||||||
| > > | let current := next(current, ROLLS); | |||||||
| let number[current] := 0; } else if number[current] <= MaxPossible[current] then { | ||||||||
| Changed: | ||||||||
| < < | # current = last(ITEMS), cutting pattern found | |||||||
| > > | # current = last(ROLLS), cutting pattern found | |||||||
| # Save the pattern | ||||||||
| Changed: | ||||||||
| < < | if ( sum {i in ITEMS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ITEMS} number[i] * Length[i] < MinLength) then { | |||||||
| > > | if ( sum {i in ROLLS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ROLLS} number[i] * Length[i] < MinLength) then { | |||||||
| let newPattern := card(PATTERNS) + 1; let PATTERNS := PATTERNS union {newPattern}; | ||||||||
| Changed: | ||||||||
| < < | let {i in ITEMS} PatternYield[newPattern, i] := number[i]; } | |||||||
| > > | let YIELDS[newPattern] := {i in ROLLS : number[i] > 0}; let {i in YIELDS[newPattern]} PatternYield[newPattern, i] := number[i]; | |||||||
| } # Increase the number cut let number[current] := number[current] + 1; } else { # Too many cut, backtrack up the tree | ||||||||
| Added: | ||||||||
| > > | print "Problem"; display current, number; | |||||||
| let number[current] := 0; | ||||||||
| Changed: | ||||||||
| < < | if current = first(ITEMS) then | |||||||
| > > | if current = first(ROLLS) then | |||||||
| let stillSearching := 0; else { | ||||||||
| Changed: | ||||||||
| < < | let current := prev(current, ITEMS); | |||||||
| > > | let current := prev(current, ROLLS); | |||||||
| let number[current] := number[current] + 1; } | ||||||||
| Added: | ||||||||
| > > | display current, number; | |||||||
| } } while stillSearching; | ||||||||
| Line: 72 to 90 | ||||||||
 | ||||||||
| Changed: | ||||||||
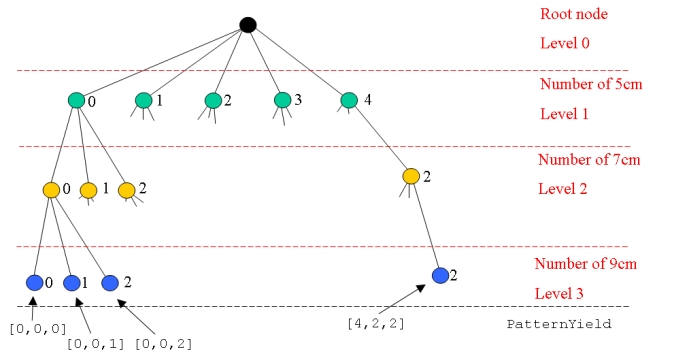
| < < | We get the maximum number of each type of roll that can be cut from the 20cm rolls from {\tt MaxPossible}. This defines the number of nodes at each level in the decision tree. | |||||||
| > > | We get the maximum number of each type of roll that can be cut from the 20cm rolls from MaxPossible. This defines the number of nodes at each level in the decision tree. | |||||||
|
We start at the root node and search on the first possibility at level 1 (the 5cm rolls):
| ||||||||
View topic | History: r6 < r5 < r4 < r3 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback