
Difference: DepthFirstSearch (1 vs. 6)
Revision 62008-05-07 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Line: 30 to 30 | ||||||||
| model; | ||||||||
| Changed: | ||||||||
| < < | reset data PatternYield, PATTERNS; # Remove any pattern data, we will find it automatically | |||||||
| > > | reset data PATTERNS, YIELDS, PatternYield; # Remove any pattern data, we will find it automatically | |||||||
| # Search the possibilities for cutting patterns param MinLength := min {i in ROLLS} Length[i]; # Find the minimum length of all the ROLLS | ||||||||
Revision 52008-05-07 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Line: 73 to 73 | ||||||||
| let number[current] := number[current] + 1; } else { # Too many cut, backtrack up the tree | ||||||||
| Deleted: | ||||||||
| < < | print "Problem"; display current, number; | |||||||
| let number[current] := 0; if current = first(ROLLS) then let stillSearching := 0; | ||||||||
| Line: 82 to 80 | ||||||||
| let current := prev(current, ROLLS); let number[current] := number[current] + 1; } | ||||||||
| Deleted: | ||||||||
| < < | display current, number; | |||||||
| } } while stillSearching; | ||||||||
| Line: 94 to 91 | ||||||||
|
We start at the root node and search on the first possibility at level 1 (the 5cm rolls):
| ||||||||
| Changed: | ||||||||
| < < | let current := first(ITEMS); | |||||||
| > > | # Start with the first product and no ROLLS being cut let current := first(ROLLS); | |||||||
| let number[current] := 0; let stillSearching := 1; | ||||||||
| Line: 103 to 101 | ||||||||
| ||||||||
| Changed: | ||||||||
| < < | if ( current <> last(ITEMS) ) and | |||||||
| > > | if ( current <> last(ROLLS) ) and | |||||||
| ( number[current] <= MaxPossible[current] ) then { | ||||||||
| Changed: | ||||||||
| < < | let current := next(current, ITEMS); | |||||||
| > > | let current := next(current, ROLLS); | |||||||
| let number[current] := 0; } | ||||||||
| Changed: | ||||||||
| < < | ||||||||
| > > | ||||||||
else if number[current] <= MaxPossible[current] then {
| ||||||||
| Changed: | ||||||||
| < < | # current = last(ITEMS), cutting pattern found | |||||||
| > > | # current = last(ROLLS), cutting pattern found | |||||||
| # Save the pattern | ||||||||
| Changed: | ||||||||
| < < | if ( sum {i in ITEMS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ITEMS} number[i] * Length[i] < MinLength) then { | |||||||
| > > | if ( sum {i in ROLLS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ROLLS} number[i] * Length[i] < MinLength) then { | |||||||
| let newPattern := card(PATTERNS) + 1; let PATTERNS := PATTERNS union {newPattern}; | ||||||||
| Changed: | ||||||||
| < < | let {i in ITEMS} PatternYield[newPattern, i] := number[i]; } | |||||||
| > > | let YIELDS[newPattern] := {i in ROLLS : number[i] > 0}; let {i in YIELDS[newPattern]} PatternYield[newPattern, i] := number[i]; | |||||||
| } # Increase the number cut let number[current] := number[current] + 1; | ||||||||
| Line: 129 to 127 | ||||||||
| else { # Too many cut, backtrack up the tree let number[current] := 0; | ||||||||
| Changed: | ||||||||
| < < | if current = first(ITEMS) then | |||||||
| > > | if current = first(ROLLS) then | |||||||
| let stillSearching := 0; else { | ||||||||
| Changed: | ||||||||
| < < | let current := prev(current, ITEMS); | |||||||
| > > | let current := prev(current, ROLLS); | |||||||
| let number[current] := number[current] + 1; } } | ||||||||
Revision 42008-05-07 - TWikiAdminUser
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Line: 12 to 12 | ||||||||
reset; | ||||||||
| Changed: | ||||||||
| < < | model cutting_stock.mod; data cutting_stock.dat; | |||||||
| > > | model cutting_stock_col.mod; data cutting_stock_col.dat; param TotalLength; param Length {ROLLS} >= 0; data; param TotalLength := 20; param Length := A 5 B 7 C 9 ; model; | |||||||
| reset data PatternYield, PATTERNS; # Remove any pattern data, we will find it automatically # Search the possibilities for cutting patterns | ||||||||
| Changed: | ||||||||
| < < | param MinLength := min {i in ITEMS} Length[i]; # Find the minimum length of all the items param MaxPossible {i in ITEMS} >= 0, integer # Find the maximum number of each length item | |||||||
| > > | param MinLength := min {i in ROLLS} Length[i]; # Find the minimum length of all the ROLLS param MaxPossible {i in ROLLS} >= 0, integer # Find the maximum number of each length item | |||||||
| := TotalLength div Length[i]; # that can be cut from a roll # The current product being considered | ||||||||
| Changed: | ||||||||
| < < | param current symbolic within ITEMS; | |||||||
| > > | param current symbolic within ROLLS; | |||||||
| # The number of each product being cut | ||||||||
| Changed: | ||||||||
| < < | param number {ITEMS} >= 0, integer, default 0; | |||||||
| > > | param number {ROLLS} >= 0, integer, default 0; | |||||||
| # Are we still searching? param stillSearching binary; | ||||||||
| Line: 33 to 48 | ||||||||
| param newPattern > 0, integer; let PATTERNS := {}; | ||||||||
| Changed: | ||||||||
| < < | # Start with the first product and no items being cut let current := first(ITEMS); | |||||||
| > > | # Start with the first product and no ROLLS being cut let current := first(ROLLS); | |||||||
| let number[current] := 0; let stillSearching := 1; repeat { display current, number; | ||||||||
| Changed: | ||||||||
| < < | if ( current <> last(ITEMS) ) and | |||||||
| > > | if ( current <> last(ROLLS) ) and | |||||||
| ( number[current] <= MaxPossible[current] ) then { | ||||||||
| Changed: | ||||||||
| < < | let current := next(current, ITEMS); | |||||||
| > > | let current := next(current, ROLLS); | |||||||
| let number[current] := 0; } else if number[current] <= MaxPossible[current] then { | ||||||||
| Changed: | ||||||||
| < < | # current = last(ITEMS), cutting pattern found | |||||||
| > > | # current = last(ROLLS), cutting pattern found | |||||||
| # Save the pattern | ||||||||
| Changed: | ||||||||
| < < | if ( sum {i in ITEMS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ITEMS} number[i] * Length[i] < MinLength) then { | |||||||
| > > | if ( sum {i in ROLLS} number[i] * Length[i] <= TotalLength) and ( TotalLength - sum {i in ROLLS} number[i] * Length[i] < MinLength) then { | |||||||
| let newPattern := card(PATTERNS) + 1; let PATTERNS := PATTERNS union {newPattern}; | ||||||||
| Changed: | ||||||||
| < < | let {i in ITEMS} PatternYield[newPattern, i] := number[i]; } | |||||||
| > > | let YIELDS[newPattern] := {i in ROLLS : number[i] > 0}; let {i in YIELDS[newPattern]} PatternYield[newPattern, i] := number[i]; | |||||||
| } # Increase the number cut let number[current] := number[current] + 1; } else { # Too many cut, backtrack up the tree | ||||||||
| Added: | ||||||||
| > > | print "Problem"; display current, number; | |||||||
| let number[current] := 0; | ||||||||
| Changed: | ||||||||
| < < | if current = first(ITEMS) then | |||||||
| > > | if current = first(ROLLS) then | |||||||
| let stillSearching := 0; else { | ||||||||
| Changed: | ||||||||
| < < | let current := prev(current, ITEMS); | |||||||
| > > | let current := prev(current, ROLLS); | |||||||
| let number[current] := number[current] + 1; } | ||||||||
| Added: | ||||||||
| > > | display current, number; | |||||||
| } } while stillSearching; | ||||||||
| Line: 72 to 90 | ||||||||
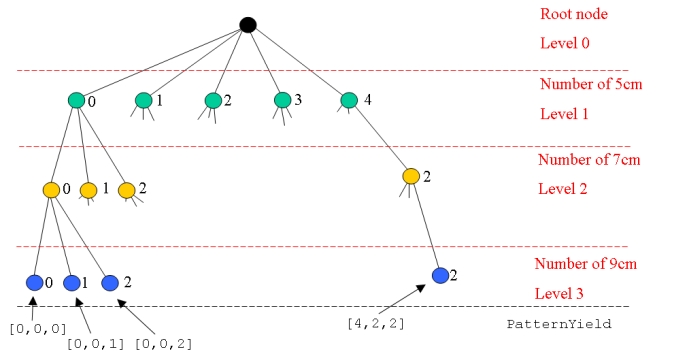 | ||||||||
| Changed: | ||||||||
| < < | We get the maximum number of each type of roll that can be cut from the 20cm rolls from {\tt MaxPossible}. This defines the number of nodes at each level in the decision tree. | |||||||
| > > | We get the maximum number of each type of roll that can be cut from the 20cm rolls from MaxPossible. This defines the number of nodes at each level in the decision tree. | |||||||
|
We start at the root node and search on the first possibility at level 1 (the 5cm rolls):
| ||||||||
Revision 32008-05-07 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Line: 70 to 70 | ||||||||
| Let's break down what is happening in detail. This code is performing a depth-first search of possible cutting patterns: | ||||||||
| Changed: | ||||||||
| < < | src="dfs_tree.jpg" | |||||||
| > > |  | |||||||
| We get the maximum number of each type of roll that can be cut from the 20cm rolls from {\tt MaxPossible}. This defines the number of nodes at each level in the decision tree. | ||||||||
| Line: 121 to 121 | ||||||||
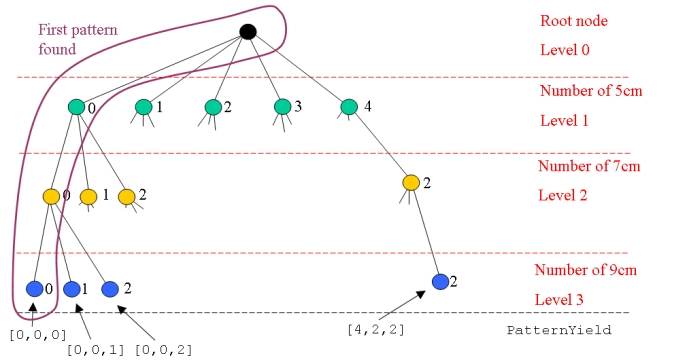
| Proceeding this way we dive to the first leaf node at the bottom left of the decision tree first: | ||||||||
| Changed: | ||||||||
| < < | src="dfs_first_pattern.jpg" | |||||||
| > > |  | |||||||
| Then move across the next possibilities at that level: | ||||||||
| Changed: | ||||||||
| < < | src="dfs_second_pattern.jpg" | |||||||
| > > | 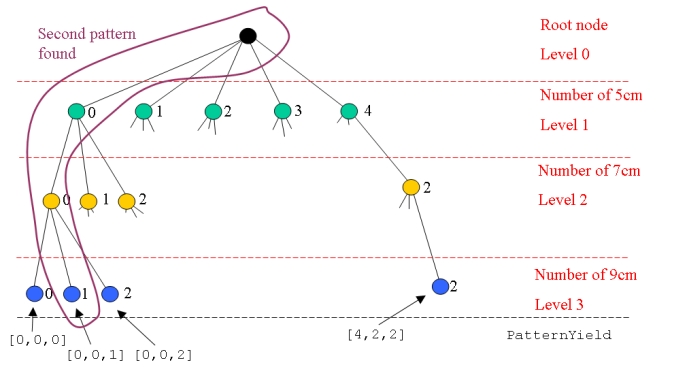 | |||||||
| Once all possibilities are exhausted we move back up the tree and move to the next possibility at that level before diving again. Finally, we will backtrack from the last leaf node (bottom right) and complete our depth-first traversal of the decision tree. -- MichaelOSullivan - 07 May 2008 | ||||||||
| Deleted: | ||||||||
| < < |
| |||||||
| ||||||||
Revision 22008-05-07 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Depth-First Search for Enumeration | ||||||||
| Added: | ||||||||
| > > | One common method of generating patterns for set partitioning problems is to use a depth-first searchDepth-First Search in AMPLDepth-first search is usually implemented using recursion, but AMPL does not have functions, so does not support recursion. However, we can implement a depth-first search non-recursively. Consider the depth-first search code from the Sponge Roll Production Problem:
reset;
model cutting_stock.mod;
data cutting_stock.dat;
reset data PatternYield, PATTERNS; # Remove any pattern data, we will find it automatically
# Search the possibilities for cutting patterns
param MinLength := min {i in ITEMS} Length[i]; # Find the minimum length of all the items
param MaxPossible {i in ITEMS} >= 0, integer # Find the maximum number of each length item
:= TotalLength div Length[i]; # that can be cut from a roll
# The current product being considered
param current symbolic within ITEMS;
# The number of each product being cut
param number {ITEMS} >= 0, integer, default 0;
# Are we still searching?
param stillSearching binary;
# Any new pattern found
param newPattern > 0, integer;
let PATTERNS := {};
# Start with the first product and no items being cut
let current := first(ITEMS);
let number[current] := 0;
let stillSearching := 1;
repeat {
display current, number;
if ( current <> last(ITEMS) ) and
( number[current] <= MaxPossible[current] ) then {
let current := next(current, ITEMS);
let number[current] := 0;
}
else if number[current] <= MaxPossible[current] then {
# current = last(ITEMS), cutting pattern found
# Save the pattern
if ( sum {i in ITEMS} number[i] * Length[i] <= TotalLength) and
( TotalLength - sum {i in ITEMS} number[i] * Length[i] < MinLength) then {
let newPattern := card(PATTERNS) + 1;
let PATTERNS := PATTERNS union {newPattern};
let {i in ITEMS} PatternYield[newPattern, i] := number[i];
}
}
# Increase the number cut
let number[current] := number[current] + 1;
}
else { # Too many cut, backtrack up the tree
let number[current] := 0;
if current = first(ITEMS) then
let stillSearching := 0;
else {
let current := prev(current, ITEMS);
let number[current] := number[current] + 1;
}
}
} while stillSearching;
Let's break down what is happening in detail. This code is performing a depth-first search of possible cutting patterns:
src="dfs_tree.jpg"
We get the maximum number of each type of roll that can be cut from the 20cm rolls from {\tt MaxPossible}. This defines the number of nodes at each level in the decision tree.
We start at the root node and search on the first possibility at level 1 (the 5cm rolls):
let current := first(ITEMS); let number[current] := 0; let stillSearching := 1;Then, we enter the loop. Each iteration through the loop starts with a node and decides where to move to from that node. There are 3 possibilities:
| |||||||
| -- MichaelOSullivan - 07 May 2008 \ No newline at end of file | ||||||||
| Added: | ||||||||
| > > |
| |||||||
Revision 12008-05-07 - MichaelOSullivan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Added: | ||||||||
| > > |
Depth-First Search for Enumeration-- MichaelOSullivan - 07 May 2008 | |||||||
View topic | History: r6 < r5 < r4 < r3 | More topic actions...
Ideas, requests, problems regarding TWiki? Send feedback