| |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
Application Areas: Data Analysis
Contents | |
<
< | | >
> | | | | Problem Description
Also known as The Least Squares Problem When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some
When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some 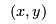 -coordinates that have a growth curve shape, i.e., initially -coordinates that have a growth curve shape, i.e., initially 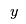 increases quickly with increases quickly with 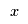 , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour: , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour:
-
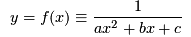
-
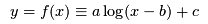
-
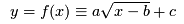
Given one of the possible functions 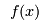 and the data points and the data points 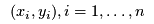 they want to find they want to find 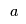 , , 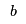 and and 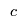 to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data. to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data. | | | Return to top
Problem Formulation | |
<
< | The formulation... | >
> |
The formulation... | | |
Return to top
Computational Model | |
<
< | The computational model... | >
> |
The computational model... | | |
Return to top
Results | |
<
< | The results... | >
> |
The results... | | |
Return to top
Conclusions | |
<
< | In conclusion... | >
> |
In conclusion... | | |
Return to top
| |
<
< | | >
> | <--
--> | | |
| |
<
< | | >
> | <--
- Write AMPL files
regression.mod and regression.run that use regression.dat to solve The Data Fitting Problem. Write a management summary of your solution. Be sure to indicate which of the functions fits the data best.
What to hand in Your new AMPL files regression.mod and regression.run. Your management summary.
--> | | | |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<-- Under Construction --> | | |
Application Areas: Data Analysis
Contents | |
<
< |
| >
> | | | | Problem Description
Also known as The Least Squares Problem When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some
When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some 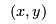 -coordinates that have a growth curve shape, i.e., initially -coordinates that have a growth curve shape, i.e., initially 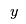 increases quickly with increases quickly with 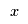 , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour: , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour:
-
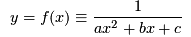
-
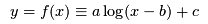
-
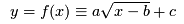
Given one of the possible functions 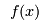 and the data points and the data points 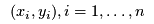 they want to find they want to find 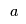 , , 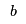 and and 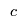 to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data.
Return to top to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data.
Return to top | |
<
< | Problem Formulation | >
> | Problem Formulation | | | | |
<
< | The formulation... | >
> | The formulation... | | | | |
<
< | Return to top
Computational Model | >
> | Return to top | | | | |
<
< | The computational model... | >
> | Computational Model | | | | |
<
< | Return to top
Results | >
> | The computational model... | | | | |
<
< | The results... | >
> | Return to top | | | | |
<
< | Return to top
Conclusions | >
> | Results | | | | |
<
< | In conclusion... | >
> | The results... | | | | |
<
< | Return to top | >
> | Return to top
Conclusions
In conclusion...
Return to top | | | | |
<
< | | >
> | | | | | |
<
< | | >
> | | | | | |
<
< | | >
> | | | | | |
<
< | Student Tasks | >
> | | | | | |
<
< |
- Write AMPL files
regression.mod and regression.run that use regression.dat to solve The Data Fitting Problem. Write a management summary of your solution. Be sure to indicate which of the functions fits the data best.
What to hand in Your new AMPL files regression.mod and regression.run. Your management summary.
| >
> | | | | | |
<
< | Return to top | >
> | | | |
| |
>
> |
| | |
|*FORM FIELD ProblemDescription*|ProblemDescription|*THE DATA FITTING PROBLEM*
Also known as The Least Squares Problem
When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some 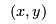 -coordinates that have a growth curve shape, i.e., initially -coordinates that have a growth curve shape, i.e., initially 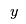 increases quickly with increases quickly with 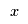 , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour: , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour:
-
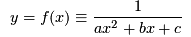
-
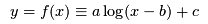
-
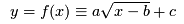
Given one of the possible functions 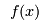 and the data points and the data points 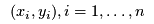 they want to find they want to find 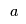 , , 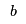 and and 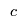 to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL ??? LINK data file =regression.dat=.
The scientists want to know which of the suggested functions provides the best fit to the data.| to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL ??? LINK data file =regression.dat=.
The scientists want to know which of the suggested functions provides the best fit to the data.| |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
| |
>
> | <-- Under Construction --> | | |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
| |
| META TOPICPARENT |
name="SubmitCaseStudy" |
|
>
> |
| META TOPICPARENT |
name="SubmitCaseStudy" |
<--
This template controls both the look and functionality of case study topics.
You should not need to alter the layout, only edit the data using the form above.
Set the view and edit templates:
Comment out the next line to use the TWiki default view
Comment out the next line to use the TWiki default edit
-->
<--
This topic can only be changed by:
-->
Submitted: 19 Feb 2008
Application Areas: Data Analysis
Contents
Problem Description
Also known as The Least Squares Problem When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some
When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some 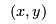 -coordinates that have a growth curve shape, i.e., initially -coordinates that have a growth curve shape, i.e., initially 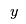 increases quickly with increases quickly with 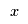 , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour: , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour:
-
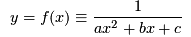
-
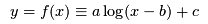
-
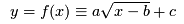
Given one of the possible functions 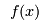 and the data points and the data points 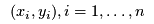 they want to find they want to find 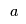 , , 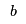 and and 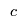 to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data.
Return to top to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL
data file regression.dat.
The scientists want to know which of the suggested functions provides the best fit to the data.
Return to top
Problem Formulation
The formulation...
Return to top
Computational Model
The computational model...
Return to top
Results
The results...
Return to top
Conclusions
In conclusion...
Return to top
Student Tasks
- Write AMPL files
regression.mod and regression.run that use regression.dat to solve The Data Fitting Problem. Write a management summary of your solution. Be sure to indicate which of the functions fits the data best.
What to hand in Your new AMPL files regression.mod and regression.run. Your management summary.
Return to top
|*FORM FIELD ProblemDescription*|ProblemDescription|*THE DATA FITTING PROBLEM*
Also known as The Least Squares Problem
When modelling data, scientists often want to fit an analytical model to their experimental data. In this case an experiment has provided some 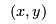 -coordinates that have a growth curve shape, i.e., initially -coordinates that have a growth curve shape, i.e., initially 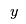 increases quickly with increases quickly with 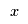 , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour: , thens tails off to some maximum value. The scientists in this study have suggested three possible functions to model this behaviour:
-
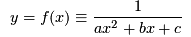
-
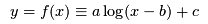
-
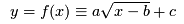
Given one of the possible functions 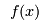 and the data points and the data points 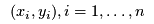 they want to find they want to find 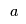 , , 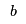 and and 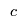 to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL ??? LINK data file =regression.dat=.
The scientists want to know which of the suggested functions provides the best fit to the data.|
|*FORM FIELD StudentTasks*|StudentTasks| 1 Write AMPL files to minimize the squared distance between the data points and the estimates, i.e.,
The scientists have specified the number of data points and their coordinates in an AMPL ??? LINK data file =regression.dat=.
The scientists want to know which of the suggested functions provides the best fit to the data.|
|*FORM FIELD StudentTasks*|StudentTasks| 1 Write AMPL files regression.mod and regression.run that use regression.dat to solve The Data Fitting Problem. Write a management summary of your solution. Be sure to indicate which of the functions fits the data best.
What to hand in Your new AMPL files regression.mod and regression.run. Your management summary.
|
| META FILEATTACHMENT |
attachment="Regression_Data.rtf" attr="" comment="" date="1203415499" name="Regression_Data.rtf" path="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\DataFitting\Regression Data.rtf" size="3617" stream="C:\Users\Lauren Jackson\Documents\Desktop\Desktop stuff\Twiki\Twiki images\DataFitting\Regression Data.rtf" tmpFilename="" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex871ec020967dc3b53d3b329cc0e111b6.png" attr="h" comment="" date="1203416375" name="latex871ec020967dc3b53d3b329cc0e111b6.png" stream="GLOB(0x8fef67c)" tmpFilename="latex871ec020967dc3b53d3b329cc0e111b6.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex837377569336c677fb59606a9dcb04c1.png" attr="h" comment="" date="1203416375" name="latex837377569336c677fb59606a9dcb04c1.png" stream="GLOB(0x87c3e8c)" tmpFilename="latex837377569336c677fb59606a9dcb04c1.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latexe900814d818af12d92934d17a5eb1fed.png" attr="h" comment="" date="1203416375" name="latexe900814d818af12d92934d17a5eb1fed.png" stream="GLOB(0x8fefee0)" tmpFilename="latexe900814d818af12d92934d17a5eb1fed.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex2c42907c743defcd93d2fff2b59d62a8.png" attr="h" comment="" date="1203416375" name="latex2c42907c743defcd93d2fff2b59d62a8.png" stream="GLOB(0x8fef94c)" tmpFilename="latex2c42907c743defcd93d2fff2b59d62a8.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex20e1cc4422656d2946847e42bd9c1934.png" attr="h" comment="" date="1203416375" name="latex20e1cc4422656d2946847e42bd9c1934.png" stream="GLOB(0x8fef4e4)" tmpFilename="latex20e1cc4422656d2946847e42bd9c1934.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex465886091365f311ad9d2a0e069a71e7.png" attr="h" comment="" date="1203416376" name="latex465886091365f311ad9d2a0e069a71e7.png" stream="GLOB(0x8fefc88)" tmpFilename="latex465886091365f311ad9d2a0e069a71e7.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex3fd969b1220a7f1752dd733f3e651f23.png" attr="h" comment="" date="1203416376" name="latex3fd969b1220a7f1752dd733f3e651f23.png" stream="GLOB(0x8fefa60)" tmpFilename="latex3fd969b1220a7f1752dd733f3e651f23.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex54524a70a68a43cd6227a154c4123445.png" attr="h" comment="" date="1203416376" name="latex54524a70a68a43cd6227a154c4123445.png" stream="GLOB(0x8efc5a8)" tmpFilename="latex54524a70a68a43cd6227a154c4123445.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latexdc67104a15b885b5c66d6b5dd957da84.png" attr="h" comment="" date="1203416376" name="latexdc67104a15b885b5c66d6b5dd957da84.png" stream="GLOB(0x8efc740)" tmpFilename="latexdc67104a15b885b5c66d6b5dd957da84.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latexa2a1c51ae440be88e5d62e8510bd7a95.png" attr="h" comment="" date="1203416376" name="latexa2a1c51ae440be88e5d62e8510bd7a95.png" stream="GLOB(0x8efc7ac)" tmpFilename="latexa2a1c51ae440be88e5d62e8510bd7a95.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latexd2a00fe0ca42ef2bb3e38b67c7b593a9.png" attr="h" comment="" date="1203416376" name="latexd2a00fe0ca42ef2bb3e38b67c7b593a9.png" stream="GLOB(0x8efc944)" tmpFilename="latexd2a00fe0ca42ef2bb3e38b67c7b593a9.png" user="LaurenJackson" version="1" |
| META FILEATTACHMENT |
attachment="latex4c436eda0e59014aa758c6ab4c0f6694.png" attr="h" comment="" date="1203416376" name="latex4c436eda0e59014aa758c6ab4c0f6694.png" stream="GLOB(0x8efca4c)" tmpFilename="latex4c436eda0e59014aa758c6ab4c0f6694.png" user="LaurenJackson" version="1" |
|
  Copyright © 2008-2026 by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding TWiki? Send feedback |
|
|
|
